RBSE Solutions for Class 6 Maths Chapter 6 पूर्णांक Ex 6.2

Rajasthan Board RBSE Solutions for Class 6 Maths Chapter 6 पूर्णांक Ex 6.2 Textbook Exercise Questions and Answers.

RBSE Class 6 Maths Solutions Chapter 6 पूर्णांक Ex 6.2

प्रश्न 1.
संख्या रेखा का प्रयोग करते हुए. वह पूर्णांक ज्ञात कीजिए जो
(a) 5 से 3 अधिक है
(b) - 5 से 5 अधिक है
(c) 2 से 6 कम है
(d) - 2 से 3 कम है।
हल:
(a) 5 से 3 बड़ा पूर्णांक प्राप्त करने के लिए हम 5 से शुरू करते हैं तथा उसके दाईं ओर 3 कदम चलते हैं तथा 8 प्राप्त करते हैं, जैसा कि निम्न आकृति में दिखाया गया है। 

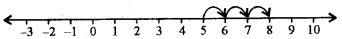
अतः 8, 5 से 3 अधिक है। 

(b)-5 से 5 बड़ा पूर्णांक प्राप्त करने के लिए हम - 5 से शुरू करते हैं तथा उसके दाईं ओर 5 कदम चलते हुए 0 पर पहुँचते हैं, जैसा कि आकृति में दिखाया गया है

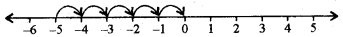
अतः 0, -5 से 5 अधिक है।

(c) 2 से 6 कम पूर्णांक प्राप्त करने के लिए हम 2 से शुरू करते हैं तथा उसके बाईं ओर 6 कदम चलते हैं तथा -4 प्राप्त करते हैं, जैसा कि निम्न आकृति में दिखाया गया है।

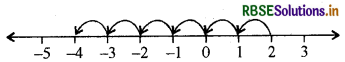
अतः - 4, 2 से 6 कम है।

(d) -2 से 3 कम पूर्णांक प्राप्त करने के लिए हम - 2 से शुरू करते हैं तथा उसके बाईं ओर 3 कदम चलते हैं तथा - 5 प्राप्त करते हैं, जैसा कि निम्न आकृति में दिखाया गया है।

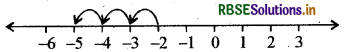
अतः - 5, -2 से 3 कम है।

प्रश्न 2.
संख्या रेखा का प्रयोग करते हुए निम्नलिखित योग ज्ञात कीजिए
(a) 9+ (-6)
(b) 5 + (-11)
(c) (-1) + (-7)
(d) (-5) + 10
(e) (-1) + (-2) + (-3)
(f) (-2) + 8 + (-4)
हल:
(a) संख्या रेखा पर पहले हम 0 के दाईं ओर 9 कदम चलते हैं और 9 पर पहुँचते हैं। तब हम 9 के बाईं ओर 6 कदम चलते हैं तथा 3 पर पहुँचते हैं, जैसा कि निम्न आकृति में दिखाया गया है।

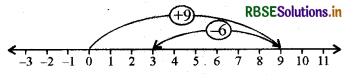
अतः 9 + (-6) = 3

(b) संख्या रेखा पर पहले हम 0 से दाईं ओर 5 कदम चलते हैं और 5 पर पहुंचते हैं। तब हम 5 के बाईं ओर 11. कदम चलते हैं तथा -6 पर पहुँचते हैं, जैसा कि निम्न आकृति में दिखाया गया है।

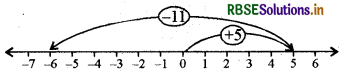
अतः 5 + (-11) = -6

(c) संख्या रेखा पर पहले हम 0 से बाईं ओर एक कदम चलते हैं और - 1 पर पहुँचते हैं। तब हम - 1 के बाईं ओर 7 कदम चलते हैं तथा -8 पर पहुँचते हैं, जैसा कि निम्न आकृति में दिखाया गया है।

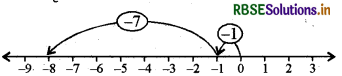
अतः (- 1) + (- 7) = -8 

(d) संख्या रेखा पर पहले हम 0 के बाईं ओर 5 कदम चलते हैं और -5 पर पहुँचते हैं। तब हम -5 के दाईं ओर 10 कदम चलते हैं तथा 5 पर पहुँचते हैं, जैसा कि निम्न आकृति में दिखाया गया है।

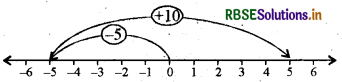
अतः (-5) + 10 = 5 

(e) संख्या रेखा पर हम 0 के बाईं ओर 1 कदम चलते हैं और - 1 पर पहुंचते हैं। तब हम - 1 के बाईं ओर 2 कदम चलते हैं तथा -3 पर पहुँचते हैं। फिर हम -3 के बाईं ओर 3 कदम चलते हैं तथा -6 पर पहुंचते हैं, जैसा कि निम्न आकृति में दिखाया गया है।

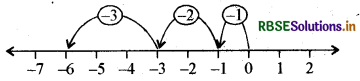
अतः (- 1) + (-2) + (-3) = - 6 

(f) संख्या रेखा पर हम 0 के बाईं ओर 2 कदम चलते हैं और - 2 पर पहुँचते हैं। तब हम - 2 के दाईं ओर 8 कदम चलते हैं तथा 6 पर पहुँचते हैं। दोबारा फिर हम 6 के बाईं ओर 4 कदम चलते हैं तथा 2 पर पहुँचते हैं, जैसा कि निम्न आकृति में दिखाया गया है।

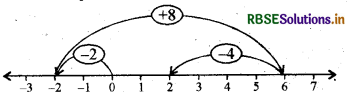
अतः (-2)+ 8 + (-4) = 2 

प्रश्न 3.
संख्या रेखा का प्रयोग किए बिना निम्नलिखित योग ज्ञात कीजिए।
(a) 11 + (-7) 
हल:
11 + (-7) = 4+7 + (-7)
= 4+ 0 = 4

(b) (-13) + (+ 18) 
हल:
(-13) + (+ 18) = (-13) + (+ 13) + (+ 5)
= 0 + (+5) = 5

(c) (-10) + (+ 19)
हल:
(-10) + (+ 19)
= (-10) + (+ 10) + (+9)
= 0 + (+9) = +9

(d) (-250) + (+ 150)
हल:
(-250) + (+ 150) = (-100) + (-150) + (+ 150)
= (- 100) + 0% - 100 

(e) (-380) + (-270)
हल:
(-380) + (-270) = - 650 

(f) (-217) + (-100)
हल:
(-217) + (-100) = -317 

प्रश्न 4.
निम्नलिखित का योग ज्ञात कीजिएहल
(a) 137 और - 354 
हल:
= (+ 137) + (-354)
= (+ 137) + (-137) + (-217)
= 0 + (-217) = - 217 

(b) -52 और 52
हल:
= (-52) + (+ 52) = 0 

(c) -312, 39 और 192 
हल:
= (-312) + (+ 39) + (+ 192)
= (-312) + (+ 231) 
= (-81) + (-231) + (+ 231)
= (-81) + 0 = -81

(d) -50, - 200 और 300
हल:
= (-50) + (-200) + (+ 300)
= (-250) + (+ 300)
= (-250) + (+ 250) + (+ 50)
= 0+ (+50) = + 50 

प्रश्न 5. 
निम्नलिखित के मान ज्ञात कीजिएहल
(a) (-7) + (-9) + 4 + 16
हल:
(-7) + (-9) + 4 + 16
= (- 16) + 4 + 16
= (-16) + (+ 16) + 4
= 0+ 4 = 4.

(b) (37) + (-2) + (-65) + (-8)
हल:
(37) + (-2) + (-65) + (-8)
= (37) + (-75)
= (+ 37) + (-37) + (-38)
= 0 + (-38) = - 38