RBSE Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes InText Questions

Rajasthan Board RBSE Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes InText Questions Textbook Exercise Questions and Answers.

RBSE Class 6 Maths Solutions Chapter 5 Understanding Elementary Shapes InText Questions

(Try These - Page 911)

Question 1.
What is the angle name for half a revolution?
Answer:
Angle of one revolution = 360°
Angle of half a revolution = 360°/2
= 180° = Straight angle
Thus, the angle of half a revolution = Straight angle

Question 2.
What is the angle name for one- fourth revolution?
Answer:
The angle name of one-fourth revolution is right angle.

Question 3.
Draw five other situations of one- fourth, half and three-fourth revolution on a clock. 
Answer:
One-fourth revolution

 

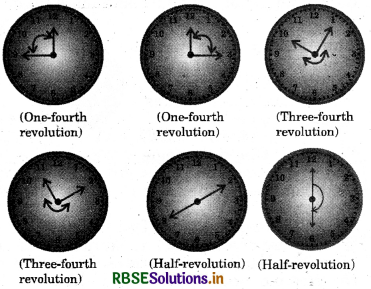
(Try These - Page 93)

Question 1.
The hour hand of a clock moves from 12 to 5. Is the revolution of the hour hand more than 1 right angle?

Answer:
Yes.

Question 2.
What does the angle made by the hour hand of the clock look like when it moves from 5 to 7. Is the angle moved more than 1 right angle?

Answer:
It looks like alphabet V. No, the angle moved is not more than 1 right angle.

Question 3.
Draw the following and check the angle with your RA tester :
(a) going from 12 to 2
(b) from 6 to 7
(c) from 4 to 8
(d) from 2 to 5.
Answer:
We know that hour hand makes total angle in one revolution (in 12 hours) = 360°.
So, hour hand makes angle in 1 hour = 360°/12 = 30°
(a) As hour hand move from 12 to 2, so that cover total hours = 12 - 2 = 10.
Then, hour hand makes angle in 10 hours = 10 x.
30° = 300°
We know : One right angle = 90°
And we can see that: 210° > 90°
So, revolution of the hour hand more than right angle.

(b) As hour hand move from 6 to 7, so that cover total hours = 7-6 = 1.
Then, hour hand makes angle in 1 hour
= 1 x 30° = 30°
We know : One right angle = 90°
And we can see that: 30° < 90°
So, revolution of the hour hand less than right angle.

(c) Do it yourself. 

(d) Do it yourself.

Question 4.
Take five different shapes with corners. Name the corners. Examine them with your tester and tabulate your results for each case :
 
(Think, Discuss and Write - Page 95)

Question 1.
How many degrees are there in half a revolution? In one right angle? In one straight angle?
How many right angles makes 180°? 360°?
Answer:
180° are there in half a revolution. In one right angle = 90°.
In one straight angle = 180°.
Two right angles make 180°.
Four right angles make 360°.

(Page 100 - Do this)

Question 1.
Using a protractor and a ruler find the measures of the sides and angles of the given triangles. Fill the measures in the given table.

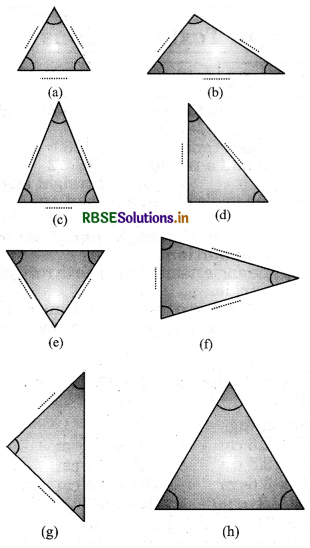
Answer:
Using protractor and ruler, measure the angles and sides of the triangle and write it in the following table:

The measure of the angles of the triangle	What can you say about the angles ?	Measures of the side
(a) 60°, 60°, 60°	All angles are equal.	All sides are equal.
(b) 50°, 95°, 35°	All angles are not equal.	All sides are not equal.
(c) 65°, 50°, 65°	Two angles are equal.	Two sides are equal.
(d) 90°, 40°, 50°	All angles are not equal.	All sides are not equal.
(e) 60°, 60°, 60°	All angles are equal.	All sides are equal.
(f) 75°, 30°, 75°	Two angles are equal.	Two sides are equal.
(g) 45°, 90°, 45°	Two angles are equal.	Two sides are equal.
(h) 60°, 60°, 60°	All angles are equal.	All sides are equal

(Do This - Page 102)

Question 1.
Try to draw rough sketches of:
(a) a scalene acute-angled triangle.
Answer:

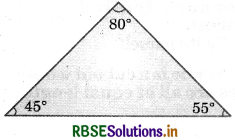
(b) an obtuse-angled isosceles triangle.
Answer:

(c) a right-angled isosceles triangle.
Answer:

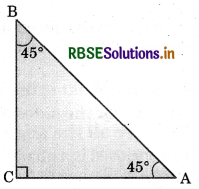
(d) a scalene right-angled triangle.
Answer:

 
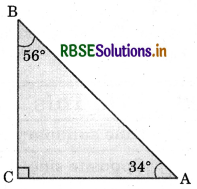
Question 2.
Do you think it is a possible to sketch :
(a) an obtuse-angled equilateral triangle?
Answer:
No, an equilateral triangle cannot have an obtuse angle. In fact, the angles are all ‘fixed’, they are each 60°.

(b) a right-angled equilateral triangle?
Answer:
No, since all the sides are equal then the angles must be equal too. So, we can’t have a right-angled equilateral triangle.

(c) a triangle with two right angles? Think, discuss and write your conclusion.
Answer:
No, if a triangle has two 90° angles, the other angle would have to be 0°. This results in a line rather than a triangle.

(Do This - Page 104)

Question 1.
Place a pair of unequal sticks such that they have their end points joined at one end. Now place another such pair meeting the free ends of the first pair. 
What is the figure enclosed ?

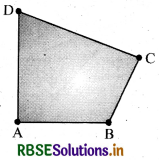
It is a quadrilateral, like the one you see here.
The sides of the quadrilateral are \(\overline{A B}, \overline{B C}\), ................., .......................... 
There are 4 angles for this quadrilateral. They are given by ∠BAD, ∠ADC, ∠DCR and ...........
\(\overline{B D}\) is one diagonal. What is the other? Measure the length of the sides and the diagonals. Measure all the angles also. 
Answer:
The figure enclosed is a quadrilateral. The sides of this quadrilateral are \(\overline{A B}, \overline{B C}, \overline{C D}, \overline{D A}\).
There are 4 angles for this quadrilateral. They are given by ∠BAD, ∠ADC, ∠DCB and ∠ABC.
\(\overline{A C}\) is one diagonal. The other diagonal is BD.

On measuring,
AB = 2.6 cm
CD = 3.5 cm
AC = 3.6 cm 
∠DAB = 90°
∠BCD = 100°

Question 2.
Using four unequal sticks, as you did in the above activity, see if you can form a quadrilateral such that:
(a) all the four angles are acute.
Answer:
No

(b) one of the angles is obtuse.
Answer:
Yes. 

(c) one of the angles is right-angled.
Answer:
Yes. 

(d) two of the angles are obtuse.
Answer:
Yes. 

(e) two of the angles are right-angled.
Answer:
Yes. 

(f) the diagonals are perpendicular to one another.
Answer:
Yes. 

(Do This - Page 106)

Question 1.
Here is an outline summary of your possible findings. Complete it. 

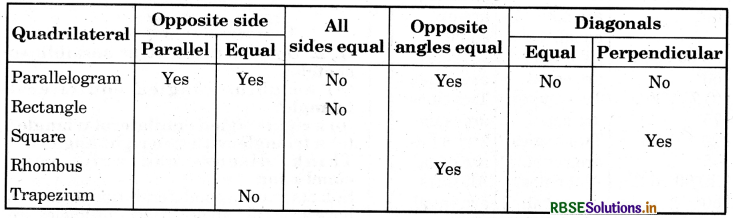
Answer:
Other properties :
(a) (i) Diagonals are equal.
(ii) Diagonals bisect each other.
(iii) Each angle is a right angle.

(b) (i) The lengths of all the sides of a square are equal. Its each angle is a right angle.
(ii) Its diagonals bisect each other.
(iii) Its diagonals bisect each other perpendicularly.

(c) (i) Yes, its opposite sides are parallel.
(ii) Yes, its opposite sides are equal.
(iii) Yes, its diagonals are not equal. 

Note: Complete the table yourself. 

(Do This - Page 110)

Question 1.
A cuboid looks like a rectangular box. It has 6 faces.
Each face has 4 edges. Each face has 4 corners (called vertices).

Answer:
Do it yourself.

Question 2.
A cube is a cuboid whose edges are all of equal length. 

It has ______ faces.
Each face has ______ edges.
Each face has ______ vertices.
Answer:
A cube is a cuboid whose all edges are of equal length.
It has 6 faces.
Each face has 4 edges.
Each face has 4 vertices.

Question 3.
A triangular pyramid has a triangle as its base. It is also known as a tetrahedron.

Faces: ______
Edges: ______
Corners : ______
Answer:
A triangular pyramid has a triangle as its base. It is also known as a tetrahedron. 
Faces : 4 
Edges : 6
Corners : 4

Question 4. 
A square pyramid has a square as its base.

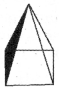
Faces:  ______
Edges : ______
Corners: ______
Answer:
A square pyramid has a square as its base.
Faces : 5
Edges : 8
Corners : 5

Question 5.
A triangular prism looks like the shape of a kaleidoscope. It has triangles as its bases.

Faces: ______
Edges : ______
Corners: ______
Answer:
A triangular prism is often of the shape of a kaleidoscope. It has triangular as its bases.
Faces : 5
Edges : 9
Corners : 6