RBSE Solutions for Class 6 Maths Chapter 3 संख्याओं के साथ खेलना Intext Questions

Rajasthan Board RBSE Solutions for Class 6 Maths Chapter 3 संख्याओं के साथ खेलना Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 6 Maths Solutions Chapter 3 संख्याओं के साथ खेलना Intext Questions

(प्रयास कीजिए पृष्ठ 51)

प्रश्न 1.
45 30 और 36 के संभावित गुणनखंड ज्ञात कीजिए।
उत्तर:
45 के संभावित गुणनखण्ड-
1, 3, 5, 9, 15 तथा 45
30 के संभावित गुणनखण्ड-
1, 2, 3, 5, 6, 10, 15 तथा 30
36 के संभावित गुणनखण्ड-
1, 2, 3, 4, 6, 9, 12, 18 तथा 36

(प्रयास कीजिए पृष्ठ 55)

प्रश्न 1.
ध्यान दीजिए कि 2 × 3 + 1 = 7 एक अभाज्य संख्या है। यहाँ 2 के एक गुणज में 1 जोड़ कर एक अभाज्य संख्या प्राप्त की गई है। क्या आप इस प्रकार से कुछ और अभाज्य संख्याएँ ज्ञात कर सकते हैं?
उत्तर:
इसी प्रकार की कुछ और संख्याएँ हैं-
2 × 1 + 1 = 3, जो कि एक अभाज्य संख्या है।
2 × 2 + 1 = 5, जो कि एक अभाज्य संख्या है।
2 × 5 + 1 = 11, जो कि एक अभाज्य संख्या है।
2 × 6 + 1 = 13, जो कि एक अभाज्य संख्या है।
2 × 8 + 1 = 17, जो कि एक अभाज्य सख्या है।
2 × 9 + 1 = 19, जो कि एक अभाज्य संख्या है।

(प्रयास कीजिए पृष्ठ 62)

प्रश्न 1.
निम्न युग्मों के उभयनिष्ठ या सार्व गुणनखंड क्या है?
(a) 8, 20
उत्तर:
8 के गुणनखण्ड हैं-1, 2, 4 और 8
20 के गुणनखण्ड हैं-1, 2, 4, 5, 10 और 20
यहाँ 8 और 20 के उभयनिष्ठ गुणनखण्ड 1, 2 और 4 हैं।

(b) 9, 15
उत्तर:
9 के गुणनखण्ड हैं-1, 3 और 9
15 के गुणनखण्ड हैं-1, 3, 5 और 15
यहाँ 9 और 15 के उभयनिष्ठ गुणनखण्ड 1 और 3 हैं।

(प्रयास कीजिए पृष्ठ 65)

प्रश्न 1.
16, 28 और 38 के अभाज्य गुणनखंडन लिखिए।
उत्तर:

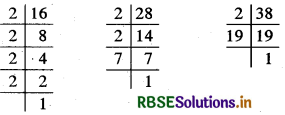
अतः अभाज्य गुणनखण्डन इस प्रकार हैं
16 = 2 × 2 × 2 × 2
28 = 2 × 2 × 7
38 = 2 × 19

(प्रयास कीजिए पृष्ठ 66)

प्रश्न 1.
निम्न का म.स. ज्ञात कीजिए
(i) 24 और 36
हल:
दी गई संख्याओं का म.स. इनके अभाज्य गुणनखण्डन द्वारा निम्न प्रकार ज्ञात किया जा सकता है|

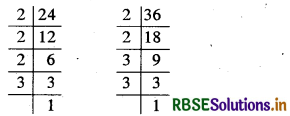
अतः 24 = 2 × 2 × 2 × 3
और 36 = 2 × 2 × 3 × 3
दी गई संख्याओं में 2 सार्व गुणनखण्ड की तरह दो बार आ रहा है और 3 सार्व गुणनखण्ड की तरह एक बार आ रहा है।
अतः अभीष्ट म.स. = 2 × 2 × 3 = 12

(ii) 15, 25 और 30
हल:

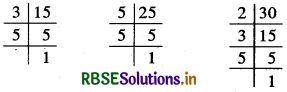
अतः 15 = 3 × 5
25 = 5 × 5
30 = 2 × 3 × 5
दी गई संख्याओं में 5 सार्व गुणनखण्ड की तरह एक बार आ रहा है।
अतः अभीष्ट म.स. = 5

(iii) 8 और 12
हल:

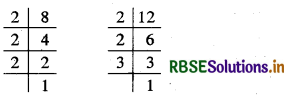
अतः 8 = 2 × 2 × 2
और 12 = 2 × 2 × 3
दी गई संख्याओं में 2 सार्व गुणनखण्ड की तरह दो बार आ रहा है।
अतः अभीष्ट म.स. = 2 × 2 = 4

(iv) 12, 16 और 28
हल:

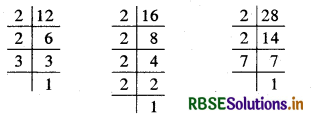
अतः 12 = 2 × 2 × 3
16 = 2 × 2 × 2 × 2
और 28 = 2 × 2 × 7
दी गई संख्याओं में 2 सार्व गुणनखण्ड की तरह दो बार आ रहा है।
अतः अभीष्ट म.स. = 2 × 2 = 4