RBSE Solutions for Class 6 Maths Chapter 3 संख्याओं के साथ खेलना Ex 3.7

Rajasthan Board RBSE Solutions for Class 6 Maths Chapter 3 संख्याओं के साथ खेलना Ex 3.7 Textbook Exercise Questions and Answers.

RBSE Class 6 Maths Solutions Chapter 3 संख्याओं के साथ खेलना Ex 3.7

प्रश्न 1.
रेणु 75 किग्रा और 69 किग्रा भारों वाली दो खाद की बोरियाँ खरीदती है। भार के उस बट्टे का अधिकतम मान ज्ञात कीजिए जो दोनों बोरियों के भारों को पूरा-पूरा माप ले।
हल:
75 किग्रा. और 69 किग्रा. खाद वाली बोरियों को मापना है। इसलिए भार इतना होना चाहिए कि वह दोनों क्षमताओं वाली बोरियों को पूरा-पूरा भाग दे। साथ ही साथ उसका मान अधिकतम होना चाहिए। इसलिए अधिकतम भार 75 और 69 का म.स. होगा।
हम देखते हैं कि

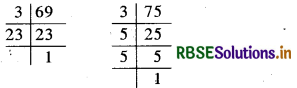
∴ 69 = 3 × 23 और 75 = 3 × 5 × 5
इस प्रकार 69 और 75 का म.स. = 3
∴ भार का अधिकतम मान = 3 किग्रा.

प्रश्न 2.
तीन लड़के एक ही स्थान से एक साथ कदम उठाकर चलना प्रारम्भ करते हैं। उनके कदमों की माप क्रमशः 63 सेमी, 70 सेमी और 77 सेमी. है। इनमें से प्रत्येक कितनी न्यूनतम दूरी तय करे कि वह दूरी पूरेपूरे कदमों में तय हो जाए?
हल:
तीन लड़के एक स्थान से एक साथ चलते हैं, और उनके कदमों की माप है क्रमशः 63 सेमी., 70 सेमी. और 77 सेमी.। प्रत्येक द्वारा पूरे-पूरे कदमों में तय की जाने वाली न्यूनतम तथा समान दूरी ज्ञात करने के लिए हम 63, 70 और 77 का ल.स: लेंगे

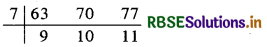
∴ ल.स. = 7 × 9 × 10 × 11 = 6930
∴ प्रत्येक द्वारा तय की गई न्यूनतम दूरी ताकि वह दूरी पूरेपूरे कदमों में तय हो जाए = 6930 सेमी. = 69.30 मी.

प्रश्न 3.
किसी कमरे की लंबाई, चौड़ाई और ऊँचाई क्रमशः 825 सेमी., 675 सेमी. और 450 सेमी. है। ऐसा सबसे लंबा फीता (tape) ज्ञात कीजिए जो कमरे की तीनों विमाओं (dimensions) को पूरा-पूरा माप ले।
हल:
सबसे बड़ा फीता (सेमी. में) जो कि तीनों विमाओं (आयामों) को पूरा-पूरा माप सके 825, 675 और 450 का म.स.. होगा।

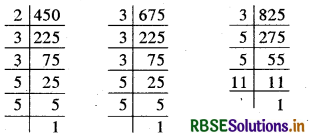
∴ 450 = 2 × 3 × 3 × 5 × 5,
675 = 3 × 3 × 3 × 5 × 5
और 825 = 3 × 5 × 5 × 11
∴ 450, 675 और 825 का म.स. = 3 × 5 × 5 = 75
∴ सबसे बड़े फीते की अभीष्ट लम्बाई = 75 सेमी.

प्रश्न 4.
6, 8 और 12 से विभाज्य तीन अंकों की सबसे छोटी संख्या ज्ञात कीजिए।
हल:
तीनों अंकों की सबसे छोटी संख्या जो 6, 8 और 12 से पूर्णतया विभाजित हो उनका ल.स. है। लेकिन हमको तीन अंकों की सबसे छोटी संख्या ज्ञात करनी है जो दी गई संख्याओं से पूर्णतया विभाजित हो । अतः ऐसी संख्या दी गई संख्याओं के ल.स. का गुणज होगी।

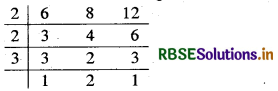
∴ ल.स. = 2 × 2 × 3 × 2 = 24
ल.स. 24 के गुणज = 24, 48, 72, 96, 120
अतः अभीष्ट संख्या = 120

प्रश्न 5.
8, 10 और 12 से विभाज्य तीन अंकों की सबसे बड़ी संख्या ज्ञात कीजिए।
हल:
8, 10 और 12 से पूर्णतया विभाज्य संख्या उनका ल. स. ही होगा। इसलिए हम सबसे पहले 8, 10 और 12 का ल.स. ज्ञात करेंगे-

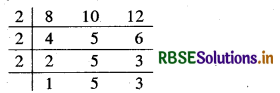
∴ ल.स. = 2 × 2 × 2 × 5 × 3 = 120
अब तीन अंकों की सबसे बड़ी संख्या = 999
999 को 120 से भाग देने पर शेष 39 आता है।
∴ 3 अंकों की सबसे बड़ी संख्या जो 8, 10 और 12 से पूर्णतया विभाज्य हो, है = 999 - 39 = 960

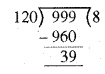
प्रश्न 6.
तीन विभिन्न चौराहों की ट्रैफिक लाइट (traffic lights) क्रमशः प्रत्येक 48 सैकंड, 72 सैकंड और 108 सैकंड बाद बदलती हैं। यदि वे एक साथ प्रातः 7 बजे बदलें, तो वे पुनः एक साथ कब बदलेंगी?

हल:
अभीष्ट समय 48, 72 और 108 का ल.स. होगा।

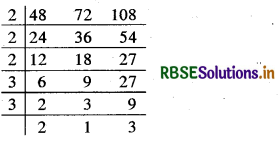
∴ ल.स. = 2 × 2 × 2 × 3 × 3 × 2 × 3 = 432
न्यूनतम अभीष्ट समय जब लाइटें दोबारा अपने आप बदलेंगी = 432 सैकंड = 432 ÷ 60 = 7 मिनट 12 सैकंड इसलिए, वे एक साथ दुबारा प्रातः 7:07:12 बजे बदलेंगी।

प्रश्न 7.
तीन टैंकरों में क्रमशः 403 लीटर, 434 लीटर और 465 लीटर डीज़ल है। उस बर्तन की अधिकतम धारिता ज्ञात कीजिए जो इन तीनों टैंकरों के डीजल को पूरा-पूरा माप देगा।
हल:
स्पष्ट है कि बर्तन की अधिकतम धारिता 403, 434 और 465 लीटर का म.स. होगा।

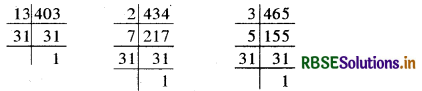
∴403 = 13 × 31, 434 = 2 × 7 × 31
और 465 = 3 × 5 × 31
∴ 403, 434 और 465 का म.स. = 31
इस प्रकार बर्तन की धारिता = 31 लीटर

प्रश्न 8.
वह सबसे छोटी संख्या ज्ञात कीजिए जिसे 6, 15 और 18 से भाग देने पर प्रत्येक दशा में 5 शेष रहे।
हल:
स्पष्ट है कि 6, 15 और 18 से विभाजित होने वाली सबसे छोटी संख्या उनका ल.स. होगी। लेकिन अभीष्ट संख्या उनके ल.स. से 5 अधिक होनी चाहिए।

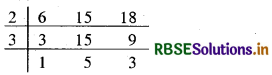
∴ ल.स. = 2 × 3 × 5 × 3 = 90
इस प्रकार अभीष्ट संख्या = (90 + 5) = 95

प्रश्न 9.
चार अंकों की वह सबसे छोटी संख्या ज्ञात कीजिए जो 18, 24 और 32 से विभाज्य है।
हल:
सबसे छोटी संख्या जो 18, 24 और 32 से विभाज्य हो उनका ल.स. है। इसलिए हम सबसे पहले 18, 24 और 32 का ल.स. ज्ञात करेंगे।

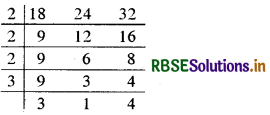
∴ ल.स. 2 × 2 × 2 × 3 × 3 × 4 = 288
अब, चार अंकों की सबसे छोटी संख्या = 1000
1000 को 288 से भाग देने पर शेष 136 आता है।

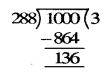
∴ 4 अंकों की सबसे छोटी संख्या जो 288 (18, 24 और 32 का ल.स.) से विभाज्य है
= 1000 + (288 - 136) = 1000 + 152 = 1152
अतएव 4 अंकों की सबसे छोटी संख्या = 1152

प्रश्न 10.
निम्नलिखित संख्याओं का ल.स. ज्ञात कीजिए जिनमें एक संख्या सदैव 3 का एक गुणज है
(a) 9 और 4
(b) 12 और 5
(c) 6 और 5
(d) 15 और 4
प्राप्त ल.स. में एक सामान्य गुण का अवलोकन कीजिए। क्या ल.स. प्रत्येक स्थिति में दोनों संख्याओं का गुणनफल है? क्या हम यह निष्कर्ष निकाल सकते हैं कि दो संख्याओं का ल.स. सदैव 3 का एक गुणज है?
हल:
सबसे पहले हम प्रत्येक संख्या का अभाज्य गुणनखण्ड करते हैं।
(a) 9 = 3 × 3 और 4 = 2 × 2
∴ ल.स. = 3 × 3 × 2 × 2 = 36
(b) 12 = 2 × 2 × 3 और 5 = 5
∴ ल.स. = 2 × 2 × 3 × 5 = 60
(c) 6 = 2 × 3 और 5 = 5
∴ ल.स. = 2 × 3 × 5 = 30
(d) 15 = 3 × 5 और 4 = 2 × 2
∴ ल.स. = 3 × 5 × 2 × 2 = 60
इस प्रकार हम देखते हैं कि सभी प्रश्नों में प्राप्त ल.स. दी गई संख्याओं का गुणनफल है क्योंकि दी गई संख्याएँ सहअभाज्य हैं। हाँ, यहाँ सभी स्थितियों में ल.स. = दो संख्याओं का गुणनफल।
हाँ, यहाँ दी गई दो-दो संख्याओं का ल.स. सदैव 3 का एक गुणज है।

प्रश्न 11.
निम्नलिखित संख्याओं का ल.स. ज्ञात कीजिए जिनमें एक संख्या दूसरी संख्या का एक गुणनखंड है
(a) 5, 20
(b) 6, 18
(c) 12,48
(d) 9, 45
प्राप्त परिणामों में आप क्या देखते हैं?
हल:
(a) 5, 20
5 = 5 और 20 = 2 × 2 × 5
∴ ल.स. = 5 × 2 × 2 = 20

(b) 6, 18 6 = 2 × 3
और 18 = 2 × 3 × 3.
∴ ल.स. = 2 × 3 × 3 = 18

(c) 12, 48 12 = 2 × 2 × 3
और 48 = 2 × 2 × 2 × 2 × 3
∴ ल.स. = 2 × 2 × 2 × 2 × 3 = 48

(d) 9, 459 = 3 × 3
और 45 = 3 × 3 × 5
∴ ल.स. = 3 × 3 × 5 = 45
इस प्रकार हम देखते हैं कि दो संख्याओं का ल.स. उनमें से बड़ी संख्या होगी यदि एक संख्या दूसरी का गुणनखण्ड है।