RBSE Solutions for Class 6 Maths Chapter 3 संख्याओं के साथ खेलना Ex 3.6

Rajasthan Board RBSE Solutions for Class 6 Maths Chapter 3 संख्याओं के साथ खेलना Ex 3.6 Textbook Exercise Questions and Answers.

RBSE Class 6 Maths Solutions Chapter 3 संख्याओं के साथ खेलना Ex 3.6

प्रश्न 1.
निम्नलिखित संख्याओं के म.स. ज्ञात कीजिए
(a) 18, 48
हल:
म.स. ज्ञात करने के लिए सबसे पहले हम दी गई संख्याओं के अभाज्य गुणनखण्डन निकालते हैं
18, 48:

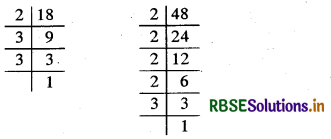
∴ 18 = 2 × 3 × 3 और 48 = 2 × 2 × 2 × 2 × 3
दी गई संख्याओं में 2 और 3 सार्व गुणनखण्ड की तरह एक-एक बार आ रहे हैं।
∴ 18 तथा 48 का म.स. = 2 × 3 = 6

(b) 30, 42
हल:
30, 42:

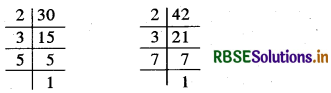
∴ 30 = 2 × 3 × 5 और 42 = 2 × 3 × 7
दी गई संख्याओं में 2 और 3 सार्व गुणनखण्ड की तरह एक-एक बार आ रहे हैं।
अतः 30 तथा 42 का म.स. = 2 × 3 = 6

(c) 18,60
हल:
18, 60

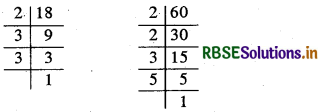
∴ 18 = 2 × 3 × 3 और 60 = 2 × 2 × 3 × 5
दी गई संख्याओं में 2 और 3 सार्व गुणनखण्ड की तरह एक-एक बार आ रहे हैं।
अतः 18 तथा 60 का म.स. = 2 × 3 = 6

(d) 27,63
हल:
27, 63

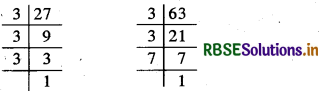
∴ 27 = 3 × 3 × 3 और 63 = 3 × 3 × 7
दी गई प्रत्येक संख्या में 3 सार्व गुणनखण्ड की तरह दो बार आ रहा है।
अतः 27 तथा 63 का म.स. = 33 × 3 = 9

(e) 36, 84
हल:
36, 84:

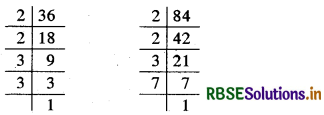
∴ 36 = 2 × 2 × 3 × 3 और 84 = 2 × 2 × 3 × 7
दी गई प्रत्येक संख्या में 2 और 3 सार्व गुणनखण्ड की तरह क्रमशः दो बार तथा एक बार आ रहे हैं।
∴ अभीष्ट म.स. = 2 × 2 × 3 = 12

(f) 34, 102
हल:
34, 102

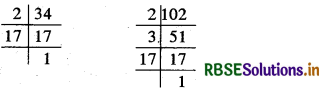
∴ 34 = 2 × 17 और 102 = 2 × 3 × 17
दी गई संख्याओं में 2 और 17 सार्व गुणनखण्ड की तरह एक-एक बार आ रहे हैं।
∴ अभीष्ट म.स. = 2 × 17 = 34

(g) 70, 105, 175
हल:
70, 105, 175:

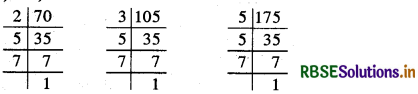
∴ 70 = 2 × 5 × 7, 105 = 3 × 5 × 7.
और 175 = 5 × 5 × 7
दी गई संख्याओं में 5 और 7 सार्व गुणनखण्ड की तरह एक-एक बार आ रहे हैं।
∴ अभीष्ट म.स. = 5 × 7 = 35

(h) 91, 112, 49
हल:
91, 112, 49

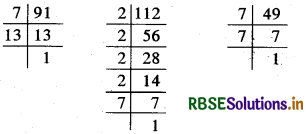
∴ 91 = 7 × 13,
112 = 2 × 2 × 2 × 2 × 7
और 49 = 7 × 7
दी गई संख्याओं में 7 सार्व गुणनखण्ड की तरह एक बार आ रहा है।
∴ अभीष्ट म.स. = 7

(i) 18, 54,81
हल:
18, 54, 81 :

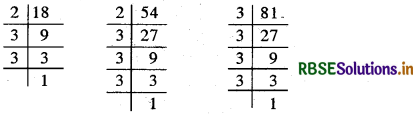
∴ 2 × 3 × 3, 54 = 2 × 3 × 3 × 3
और 81 = 3 × 3 × 3 × 3
दी गई संख्याओं में 3 सार्व गुणनखण्ड की तरह दो बार आ रहा है।
∴ अभीष्ट म.स. = 3 × 3 = 9

(j) 12, 45, 75
हल:
12, 45, 75:

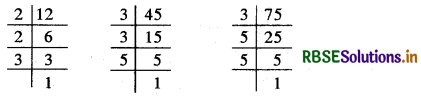
∴ 12 = 2 × 2 × 3, 45 = 3 × 3 × 5 और 75 = 3 × 5 × 5
दी गई संख्याओं में 3 सार्व गुणनखण्ड की तरह एक बार आ रहा है।
∴ अभीष्ट म.स. = 3

प्रश्न 2.
निम्न का म.स. क्या है?
(a) दो क्रमागत संख्याएँ
हल:
दो क्रमागत संख्याओं का म.स. = 1

(b) दो क्रमागत सम संख्याएँ
हल:
दो क्रमागत सम संख्याओं का म.स. = 2

(c) दो क्रमागत विषम संख्याएँ।
हल:
दो क्रमागत विषम संख्याओं का म.स. = 1

प्रश्न 3.
अभाज्य गुणनखंडन द्वारा दो सह-अभाज्य संख्याओं 4 और 15 का म.स. इस प्रकार ज्ञात किया गया
4 = 2 × 2 और 15 = 3 × 5
चूँकि इन गुणनखंडों में कोई अभाज्य सार्व गुणनखंड नहीं है, इसलिए 4 और 15 का म.स. शून्य है। क्या यह उत्तर सही है? यदि नहीं तो सही म.स. क्या है?
हल:
नहीं, यह उत्तर गलत है। दो सह-अभाज्य संख्याओं 4 और 15 का सही म.स. 1 है।