RBSE Solutions for Class 6 Maths Chapter 3 संख्याओं के साथ खेलना Ex 3.5

Rajasthan Board RBSE Solutions for Class 6 Maths Chapter 3 संख्याओं के साथ खेलना Ex 3.5 Textbook Exercise Questions and Answers.

RBSE Class 6 Maths Solutions Chapter 3 संख्याओं के साथ खेलना Ex 3.5

प्रश्न 1.
निम्नलिखित में से कौन-से कथन सत्य हैं?
(a) यदि कोई संख्या 3 से विभाज्य है, तो वह 9 से भी विभाज्य होती है।
(b) यदि एक संख्या 9 से विभाज्य है, तो वह 3 से भी अवश्य विभाज्य होगी।
(c) एक संख्या 18 से भी विभाज्य होती है, यदि वह 3 और 6 दोनों से विभाज्य हो।
(d) यदि एक संख्या 9 और 10 दोनों से विभाज्य हो, तो वह 90 से भी विभाज्य होगी।
(e) यदि दो संख्याएँ सह-अभाज्य हों, तो इनमें से कम से कम एक अवश्य ही अभाज्य संख्या होगी।
(f) 4 से विभाज्य सभी संख्याएँ 8 से भी अवश्य विभाज्य होनी चाहिए।
(g) 8 से विभाज्य सभी संख्याएँ 4 से विभाज्य होनी चाहिए।
(h) यदि कोई संख्या दो संख्याओं को अलग-अलग पूरा पूरा विभाजित करती है, तो वह उनके योग को भी पूरापूरा विभाजित करेगी।
(i) यदि कोई संख्या दो संख्याओं के योग को पूरी तरह विभाजित करती है, तो वह उन दोनों संख्याओं को अलगअलग भी विभाजित करेगी।
उत्तर:
सत्य कथन-(b), (d), (g), (h)

प्रश्न 2.
यहाँ 60 के लिए दो भिन्न-भिन्न गुणनखंड वृक्ष दिए हैं। इनमें अज्ञात संख्याएँ लिखिए।
(a)

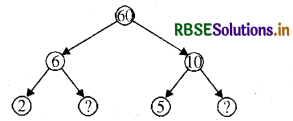
हल:
अज्ञात संख्याएँ 3 और 2 हैं। .
∵ 6 = 2 × 3 और 10 = 5 x 2

(b)

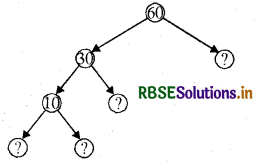
हल:
अज्ञात संख्याएँ 2; 3; 2 और 5 हैं।
∵ 60 = 30 × 2
30 = 10 × 3
और 10 = 2 × 5

प्रश्न 3.
एक भाज्य संख्या के अभाज्य गुणनखंडन में किन गुणनखंडों को सम्मिलित नहीं किया जाता है?
हल:
एक भाज्य संख्या के अभाज्य गुणनखण्डन में 1 तथा स्वयं उस संख्या को सम्मिलित नहीं किया जाता है।

प्रश्न 4.
चार अंकों की सबसे बड़ी संख्या लिखिए और उसे अभाज्य गुणनखंडन के रूप में व्यक्त कीजिए।
हल:
चार अंकों की सबसे बड़ी संख्या = 9999

अतः 9999 का अभाज्य गुणनखण्डन = 3 × 3 × 11 × 101

प्रश्न 5.
पाँच अंकों की सबसे छोटी संख्या लिखिए और उसे अभाज्य गुणनखंडन के रूप में व्यक्त कीजिए।
हल:
पाँच अंकों की सबसे छोटी संख्या = 10000

अतः 10000 का अभाज्य गुणनखण्डन = 2 × 2 × 2 × 2 × 5 × 5 × 5 × 5

प्रश्न 6.
1729 के सभी अभाज्य गुणनखंड ज्ञात कीजिए और उन्हें आरोही क्रम में व्यवस्थित कीजिए। अब दो क्रमागत अभाज्य गुणनखंडों में यदि कोई संबंध है तो लिखिए।
हल:

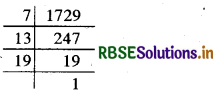
अतः 1729 के अभाज्य गुणनखण्ड = 7 × 13 × 19
स्पष्टतः दो क्रमागत अभाज्य गुणनखण्डों के बीच 6 का अन्तर है।

प्रश्न 7.
तीन क्रमागत संख्याओं का गुणनफल सदैव 6 से विभाज्य होता है। इस कथन को कुछ उदाहरणों की सहायता से स्पष्ट कीजिए।
हल:
कुछ तीन क्रमागत संख्याओं का गुणनफल
1 × 2 × 3 = 6
2 × 3 × 4 = 24
3 × 4 × 5 = 60
11 × 12 × 13 = 1716
17 × 18 × 19 = 5814
20 × 21 × 22 = 9240
प्रत्येक गुणनफल में इकाई का अंक 6, 4 या 0 है।
इसलिए प्रत्येक गुणनफल 2 से विभाज्य है और इन गुणनफलों के अंकों का योग 3 से भी विभाज्य है। इसलिए प्रत्येक गुणनफल 3 से विभाज्य है।
जैसा कि 2 और 3 सह-अभाज्य हैं, इसलिए 2 × 3 = 6 ऊपर के प्रत्येक गुणनफल को विभाजित करेगा।
इसलिए तीन क्रमागत संख्याओं का गुणनफल सदैव 6 से विभाज्य है।

प्रश्न 8.
दो क्रमागत विषम संख्याओं का योग 4 से विभाज्य होता है। कुछ उदाहरण लेकर इस कथन का सत्यापन कीजिए।
उत्तर:
दो क्रमागत विषम संख्याओं का योग
3 + 5 = 8,
5 + 7 = 12,
11 + 13 = 24,
23 + 25 = 48,
51 + 53 = 104,
69 + 71 = 140
स्पष्टतः ऊपर दी गई दो क्रमागत विषम संख्याओं का प्रत्येक योग 4 से विभाजित हो रहा है। अतः यह सत्य है. कि दो क्रमागत विषम संख्याओं का योग 4 से विभाज्य होता है।

प्रश्न 9.
निम्न में से किन व्यंजकों में अभाज्य गुणनखंडन किए गए हैं
(a) 24 = 2 × 3 × 4
(b) 56 = 1 × 7 × 2 × 2 × 2
(c) 70 = 2 × 5 × 7
(d) 54 = 2 × 3 × 9
हल:
(b) और (c) में अभाज्य गुणनखण्डन किए गए हैं

प्रश्न 10.
बिना भाग किए ज्ञात कीजिए कि क्या 25110 संख्या 45 से विभाज्य है।
[संकेत : 5 और 9 सह-अभाज्य संख्याएँ हैं। दी हुई संख्या की 5 और 9 से विभाज्यता की जाँच कीजिए ।]
हल:
जैसा कि 45 = 5×9, जहाँ 5 और 9 सह-अभाज्य हैं। इसलिए 25110 की 45 से विभाज्यता जाँचने के लिए इसकी जाँच 5 और 9 से करेंगे-
25110 में इकाई का अंक = 0
इसलिए यह 5 से विभाज्य है।
25110 में अंकों का योग = 2 + 5 + 1 + 1 + 0 = 9, जो कि 9 से विभाज्य है।
इसलिए 25110, 9 से भी विभाज्य है।
इस प्रकार 25110 संख्या 45 से विभाज्य है।

प्रश्न 11.
संख्या 18, 2 और 3 दोनों से विभाज्य है। यह 2 × 3 = 6 से भी विभाज्य है। इसी प्रकार, एक संख्या 4 और 6 दोनों से विभाज्य है। क्या हम कह सकते हैं कि यह संख्या 4 × 6 = 24 से भी विभाज्य होगी? यदि नहीं, तो अपने उत्तर की पुष्टि के लिए एक उदाहरण दीजिए।
हल:
यदि कोई संख्या 4 और 6 दोनों से विभाज्य है तो जरूरी नहीं है कि वह 4 × 6 = 24 से भी विभाज्य हो। क्योंकि 12, 36,60 आदि कुछ ऐसी संख्याएँ हैं जो 4 और 6 दोनों से विभाज्य हैं लेकिन 4 × 6 = 24 से विभाज्य नहीं हैं। ऐसा इसलिए है क्योंकि 4 और 6 सह-अभाज्य संख्याएँ नहीं हैं।

प्रश्न 12.
मैं चार भिन्न-भिन्न अभाज्य गुणनखंडों वाली सबसे छोटी संख्या हूँ। क्या आप मुझे ज्ञात कर सकते
हल:
चार भिन्न-भिन्न अभाज्य छोटी संख्याएँ 2, 3, 5 और 7 हैं।
अतः अभीष्ट संख्या = 2 × 3 × 5 × 7 = 210