RBSE Solutions for Class 6 Maths Chapter 2 पूर्ण संख्याएँ Intext Questions
Rajasthan Board RBSE Solutions for Class 6 Maths Chapter 2 पूर्ण संख्याएँ Intext Questions Textbook Exercise Questions and Answers.
Rajasthan Board RBSE Solutions for Class 6 Maths in Hindi Medium & English Medium are part of RBSE Solutions for Class 6. Students can also read RBSE Class 6 Maths Important Questions for exam preparation. Students can also go through RBSE Class 6 Maths Notes to understand and remember the concepts easily. Students are advised to practice अनुपात और समानुपात के प्रश्न class 6 of the textbook questions.
RBSE Class 6 Maths Solutions Chapter 2 पूर्ण संख्याएँ Intext Questions
(प्रयास कीजिए। - पृष्ठ 29)
प्रश्न 1.
19; 1997; 12000; 49; 100000; 2440701; 100199 और 208090 के पूर्ववर्ती और परवर्ती लिखिए।
उत्तर:
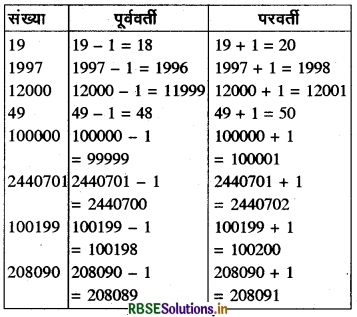
प्रश्न 2.
क्या कोई ऐसी प्राकृत संख्या है, जिसका कोई पूर्ववर्ती नहीं है?
उत्तर:
हाँ, प्राकृत संख्या 1 का कोई पूर्ववर्ती नहीं है।
प्रश्न 3.
क्या कोई ऐसी प्राकृत संख्या है, जिसका कोई परवर्ती नहीं है? क्या कोई अंतिम प्राकृत संख्या है?
उत्तर:
नहीं, ऐसी कोई प्राकृत संख्या नहीं है, जिसका कोई परवर्ती नहीं है, और न ही कोई भी अन्तिम प्राकृत संख्या है

(प्रयास कीजिए। - पृष्ठ 30)
प्रश्न 1.
क्या सभी प्राकृत संख्याएँ पूर्ण संख्याएँ भी हैं?
उत्तर:
हाँ, सभी प्राकृत संख्याएँ पूर्ण संख्याएँ भी हैं।
प्रश्न 2.
क्या सभी पूर्ण संख्याएँ प्राकृत संख्याएँ भी हैं?
उत्तर:
नहीं, सभी पूर्ण संख्याएँ प्राकृत संख्याएँ नहीं हैं। 0 एक पूर्ण संख्या है जो प्राकृत संख्या नहीं है।
प्रश्न 3.
सबसे छोटी पूर्ण संख्या कौन-सी है?
उत्तर:
0 सबसे छोटी पूर्ण संख्या है।
प्रश्न 4.
सबसे बड़ी पूर्ण संख्या कौन-सी है?
उत्तर:
किसी भी पूर्ण संख्या में 1 जोड़कर उससे बड़ी पूर्ण संख्या ज्ञात की जा सकती है। अतः कोई भी पूर्ण संख्या सबसे बड़ी नहीं है।
(प्रयास कीजिए। - पृष्ठ 31)
प्रश्न 1.
संख्या रेखा का प्रयोग करके 4+5; 2 + 6; 3 + 5 और 1 + 6 को ज्ञात कीजिए।
हल:
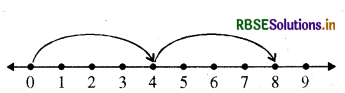
4+5

तीर के सिरे पर बिन्दु 4 है। 4 से प्रारम्भ कीजिए, चूंकि हमें इस संख्या में 5 जोड़ना है, इसलिए हम दाईं ओर 5 कदम 4 से 5,5 से 6, 6 से 7,7 से 8 और 8 से 9 चलते हैं। जैसा कि ऊपर दिखाया गया है। पाँचवें कदम के अन्तिम तीर के सिरे पर बिन्दु 9 है। अतः 4+ 5 = 9
2+6

तीर के सिरे पर बिन्दु 2 है। 2 से प्रारम्भ करें, चूँकि हमें इस संख्या में 6 जोड़ना है, इसलिए हम दाईं ओर 6 कदम 2 से 3, 3 से 4, 4 से 5, 5 से 6, 6 से 7 और 7 से 8 चलते हैं। जैसा कि ऊपर दिखाया गया है। छठे कदम के अन्तिम तीर के सिरे पर बिन्दु 8 है। अतः 2 + 6 = 8
3+5

तीर के सिरे पर बिन्दु 3 है। 3 से प्रारम्भ कीजिए। चूंकि हमें 5 जोड़ना है, इसलिए हम दाईं ओर 5 कदम 3 से 4, 4 से 55 से 6.6 से 7 और 7 से 8 चलते हैं। जैसा कि ऊपर दिखाया गया है। पाँचवें कदम के अन्तिम तीर के सिरे पर बिन्दु 8 है। . अतः 3 + 5 = 8
1+ 6

तीर के सिरे पर बिन्दु 1 है। 1 से प्रारम्भ कीजिए। चूंकि हमें इस संख्या में 6 जोड़ना है इसलिए हम दाईं ओर 6 कदम 1 से 2, 2 से 3, 3 से 4, 4 से 5, 5 से 6 और 6 से 7 चलते हैं। जैसा कि ऊपर दिखाया गया है। छठे कदम के अन्तिम तीर के सिरे पर बिन्दु 7 है। अत: 1 + 6 = 7

(प्रयास कीजिए। - पृष्ठ 32-I)
प्रश्न 1.
संख्या रेखा का प्रयोग करके 8-3; 6 - 2 और 9-6 ज्ञात कीजिए।
हल:
8 - 3

तीर के सिरे पर बिन्दु 8 है। 8 से प्रारम्भ कीजिए। चूंकि 3 को घटाया जाना है, इसलिए हम बाईं ओर 1. मात्रक वाले तीन कदम चलते हैं। ऐसे 3 कदम चलने पर हम बिन्दु 5 पर पहुंचते हैं। अतः 8 -3 = 5
6-2
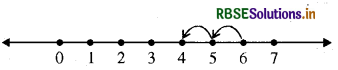
तीर के सिरे पर बिन्दु 6 है। 6 से प्रारम्भ कीजिए। चूंकि 2 को घटाया जाना है, इसलिए हम बाईं ओर 1 मात्रक वाले दो कदम चलते हैं। ऐसे 2 कदम चलने पर हम । बिन्दु 4 पर पहुंचते हैं। अतः 6-2 = 4
9-6

तीर के सिरे पर बिन्दु 9 है। 9 से प्रारम्भ कीजिए। चूंकि 6 को घटाया जाना है, इसलिए हम बाईं ओर 1 मात्रक वाले 6 कदम चलते हैं। ऐसे 6 कदम चलने पर हम बिन्दु 3 पर पहुंचते हैं। अतः 9 - 6 = 3
(प्रयास कीजिए - पृष्ठ 32-II)
प्रश्न 1.
संख्या रेखा का प्रयोग करके 2 × 6; 3 × 3 और 4 × 2 को ज्ञात कीजिए।
हल:
2 × 6
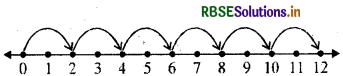
0 से प्रारम्भ कीजिए, और दाईं ओर एक बार में 2 मात्रकों के बराबर के कदम चलिए। ऐसे 6 कदम चलने पर हम बिन्दु 12 पर पहुँचते हैं। अतः 2 × 6 = 12
3 × 3
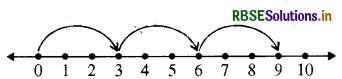
0 से प्रारम्भ कीजिए, और दाईं ओर एक बार में 3 मात्रंकों के बराबर के कदम चलिए। ऐसे 3 कदम चलने पर हम बिन्दु 9 पर पहुंचते हैं। अतः 3 × 3 = 9
4 × 2
0 से प्रारम्भ कीजिए, और दाईं ओर एक बार में 4 मात्रकों के बराबर के कदम चलिए। ऐसे 2 कदम चलने पर हम बिन्दु 8 पर पहुँचते हैं । अतः 4 × 2 = 8
(जाँच कीजिए। - पृष्ठ 37)
प्रश्न 1.
(i) पूर्ण संख्याओं के लिए, व्यवकलन (घटाना) क्रमविनिमेय नहीं है। इसकी जाँच संख्याओं के तीन विभिन्न युग्म लेकर कीजिए।
(ii) क्या (6 ÷ 3) वही है जो (3 ÷ 6) है?
पूर्ण संख्याओं के कुछ और युग्म लेकर अपने उत्तर की पुष्टि कीजिए।
हल:
(i) पूर्ण संख्याओं के लिए व्यवकलन (घटाना) क्रमविनिमेय नहीं है। यदि a तथा b दो पूर्ण संख्याएँ तो सामान्यतया (a - b), (b - a) के बराबर नहीं होता।
जाँच:
(1)8 -5 = 3 लेकिन 5-8 सम्भव नहीं है।
(2) 25 - 13 = 12 लेकिन 13 - 25 सम्भव नहीं है।
(3) 125 - 110 = 15 लेकिन 110 - 125 सम्भव नहीं है।
अंतः पूर्ण संख्याओं के लिए घटाना क्रमविनिमेय नहीं है।
(ii) 6 ÷ 3 = 2 तथा 3 ÷ 6 = \frac{1}{2}.
अतः 6 ÷ 3 ≠ 3 ÷ 6
उत्तर की जाँच
(1) 20 ÷ 10 = 2 तथा 10 ÷ 20 =\frac{1}{2}
अतः 20 ÷ 10 ≠ 10 ÷ 20
(2) 18 ÷ 6 = 3 तथा 6 ÷ 18 = \frac{1}{3}
अतः 18 ÷ 6 ≠ 6 ÷ 18
(3). 100 ÷ 25 = 4 तथा 25 ÷ 100 = \frac{1}{4}
अतः 100 ÷ 25 + 25 ÷ 100
(प्रयास कीजिए। - पृष्ठ 39)
प्रश्न 1.
7 + 18 + 13 और 16 + 12 + 4 को ज्ञात कीजिए।
हल:
(1) 7+ 18 + 13 = (7 + 18) + 13
= 25 + 13 = 38
तथा 7 + 18 + 13 = (7 + 13) + 18
= 20 + 18 = 38
(2) 16 + 12 + 4 = (16 + 12) + 4
= 28 + 4 = 32
तथा 16 + 12 + 4 = (16 + 4) + 12
= 20 + 12 = 32

(प्रयास कीजिए - पृष्ठ 39-II)
प्रश्न 1.
ज्ञात कीजिए 25 × 8358 × 4; 625 × 3759 × 8
हल:
(1) 25 × 8358 × 4= 25 × 4 × 8358 [गुणन साहचर्य]
= 100 × 8358 = 835800
(2) 625 × 3759 × 8 = 625 × 8 × 3759 [गुणन साहचर्य]
= 5000 × 3759
= 18795000
(सोचिए, चर्चा कीजिए और लिखिए - पृष्ठ 39)
प्रश्न 1.
क्या (16 ÷ 4) 2 = 16 (4 ÷ 2) है? क्या विभाजन के लिए साहचर्य गुण लागू होता है? नहीं। अपने मित्रों के साथ चर्चा कीजिए। क्या (28 ÷ 14) ÷ 2 और 28 ÷ (14 ÷ 2) बराबर हैं?
हल:
नहीं, ये बराबर नहीं हैं।
(16 ÷ 4)2 = (4) ÷ 2 = 4 ÷ 2 = 2
तथा 16 ÷ (4 ÷ 2) = 16 ÷ (2) = 16 ÷ 2 = 8
अतः (16 ÷ 4) ÷ 2 + 16 ÷ (4 ÷ 2)
अतः भाग करने के लिए कोई साहचर्य गुण नहीं है।
पुनः, (28 ÷ 14): 2 = (2) ÷ 2 = 2 ÷ 2 = 1
तथा 28 ÷ (14 ÷ 2) = 28 ÷ (7)
= 28 ÷ 7 = 4
अतः (28 ÷ 14) ÷ 2 ≠ 28 ÷ (14 - 2)
अतः विभाजन के लिए साहचर्य गुण लागू नहीं होता।
(प्रयास कीजिए - पृष्ठ 41)
प्रश्न 1.
वितरण गुण का प्रयोग करते हुए, 15 × 68, 17 × 23 और 69 × 78 + 22 × 69 के मान ज्ञात कीजिए।
हल:
(1) 15 × 68 ज्ञात करने के लिएवितरण गुण का प्रयोग करते हुए
15 × 68 = 15 × (60 + 8)
= 15 × 60 + 15 × 8
= 900 + 120 = 1020
(2) 17 × 23 ज्ञात करने के लिएवितरण गुण का प्रयोग करते हुए.
17 × 23 = 17 × (20 + 3)
= 17 × 20 + 17 × 3
= 340 + 51 = 391
(3) 69 × 78 + 22 × 69 ज्ञात करने के लिए
69 × 78 + 22 × 69 = 69 × (78 + 22)
= 69 × 100 = 6900
(प्रयास कीजिए। - पृष्ठ 44)
प्रश्न 1.
कौन-सी संख्याएँ केवल रेखा के रूप में दर्शाई जा सकती हैं?
उत्तर:
2, 5, 7, 11, 13, .... संख्याएँ केवल रेखा के रूप में दर्शाई जा सकती हैं।
प्रश्न 2.
कौन-सी संख्याएँ वर्गों के रूप में दर्शाई जा सकती हैं?
उत्तर:
4, 9, 16, 25, .... संख्याएँ वर्गों के रूप में दर्शाई जा सकती हैं।
प्रश्न 3.
कौन-सी संख्याएँ आयतों के रूप में दर्शाई जा सकती हैं?
उत्तर:
4, 6, 8, 9, 10, 12, .... संख्याएँ आयतों के रूप में दर्शाई जा सकती हैं।
प्रश्न 4.
प्रथम सात त्रिभुजाकार संख्याओं को लिखिए (अर्थात् वे संख्याएँ जिन्हें त्रिभुजों के रूप में व्यवस्थित किया जा सकता है) 3, 6,...
उत्तर:
प्रथम सात त्रिभुजाकार संख्याएँ हैं3, 6, 10, 15, 21, 28 और 36

प्रश्न 5.
कुछ संख्याओं को दो आयतों के रूप में दर्शाया जा सकता है। उदाहरणार्थ,

इसी प्रकार के कम से कम पाँच उदाहरण दीजिए।
उत्तर:
12 के अलावा 5 संख्याएँ जिनको कि दो आयतों द्वारा दिखाया जा सकता है
16 → 2 × 8, 4 × 4;
18 → 3 × 6, 2 × 9;
20 → 2 × 10, 4 × 5;
24 →3 × 8, 4 × 6;
28 → 2 × 14, 4 × 7

- RBSE Solutions for Class 6 Maths Chapter 2 Whole Numbers InText Questions
- RBSE Class 6 Maths Important Questions Chapter 1 अपनी संख्याओं की जानकारी
- RBSE Solutions for Class 6 Maths Chapter 7 भिन्न Intext Questions
- RBSE Solutions for Class 6 Maths Chapter 7 Fractions Ex 7.4
- RBSE Solutions for Class 6 Maths Chapter 1 Knowing our Numbers Ex 1.1
- RBSE Solutions for Class 6 Maths Chapter 1 Knowing our Numbers InText Questions
- RBSE Solutions for Class 6 Maths in Hindi Medium & English Medium
- RBSE Solutions for Class 6 Maths Chapter 7 Fractions InText Questions
- RBSE Solutions for Class 6 Maths Chapter 7 Fractions Ex 7.6
- RBSE Solutions for Class 6 Maths Chapter 7 Fractions Ex 7.5
- RBSE Solutions for Class 6 Maths Chapter 7 Fractions Ex 7.3