RBSE Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.5

Rajasthan Board RBSE Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.5 Textbook Exercise Questions and Answers.

RBSE Class 6 Maths Solutions Chapter 14 Practical Geometry Ex 14.5

Question 1.
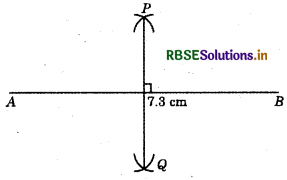
Draw \(\overline{A B}\) of length 7.3 cm and find its axis of symmetry.
Answer:
The axis of symmetry of a line segment will be the perpendicular bisector of it: 

1. Draw a line segment \(\overline{A B}\) of length 7.3 cm.
2. Open the compasses more than half of length \(\overline{A B}\).
3. Allow with centres A and B, draw two arcs which intersect each other at P and Q.
4. Join P and Q.

Thus, PQ is the axis of symmetry of AB.

 
Question 2.
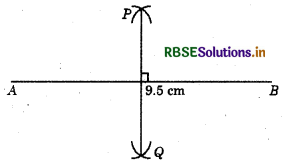
Draw a line segment of length 9.5 cm and construct its perpendicular bisector. .
Answer:
Steps of construction :

1. Draw a line segment AB of length 9.5 cm.
2. By taking radius more than half of AB, draw two arcs by taking A and B as centres.
3. Let these arcs intersect each other at P and Q.
4. Join PQ. This PQ is the required perpendicular bisector of AB.

Question 3.
Draw the perpendicular bisector of \( \overline{X Y}\) whose length is 10.3 cm :
(a) Take any point P on the bisector drawn. Examine whether PX = PY.
(b) If M is the mid point \( \overline{X Y}\), what can you say about the lengths MX and XY?
Answer:
Step 1: Draw a line segment \( \overline{X Y}\) of length 10.3 cm.
Step 2 : By taking radius more than half of length of AB, draw two arcs from X and Y. Let these arcs intersect each other at A and B.

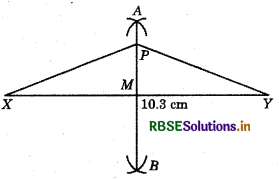
Step 3 : Join A and B.
Step 4: Mark a point P on AB, join PX and PY.
(a) By measuring PX and PY, we find that PX = PY.
(b) Since, M is a mid-point of XY on measuring, we have MX = \(\frac{1}{2}\) XY.

Question 4. 
Draw a line segment of length 12.8 cm. Using compasses, divide it into four equal parts. Verify by actual measurement.
Answer:
Steps of construction :
1. Draw a line segment AB of length 12.8 cm.  
2. Draw perpendicular bisector of \(\overline{A B}\), which meets \(\overline{A B}\) at O, i.e. O is the mid-point of \overline{A B}.

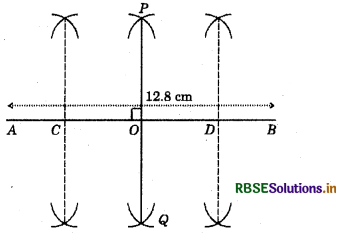
3. Draw the perpendicular bisector of AO, which meets AB at C, i.e. C is the mid-point of AO.
4. Draw the perpendicular bisector of OB, which meets AB at D, i.e. D is the mid-point of OB.
By measuring two lengths AC, CO, OD and DB, we get AC = CO = OD = DB

Question 5.
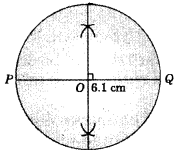
With \(\overline{P Q}\) of length 6.1 cm as diameter, draw a circle.
Answer:
Steps of construction :

1. Draw a line segment \(\overline{P Q}\) of length 6.1 cm.
2. Draw the perpendicular bisector of PQ which intersect \(\overline{P Q}\) at O.
3. Now by taking O as a center and OP as radius, draw a circle. This circle having \(\overline{P Q}\) as diameter is the required circle.

Question 6.
Draw a circle with centre C and radius 3.4 cm. Draw any chord AB. Construct the perpendicular bisector of \(\overline{A B}\) and examine if it passes through C.
Answer:
Steps of construction :

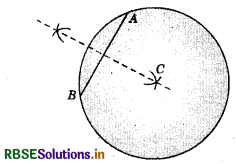
1. By taking C as center, draw a circle of radius 3.4 cm.
2. Draw a chord AB.
3. Draw the perpendicular bisector of chord AB, we find that it passes through the centre of circle.    

Question 7.
Repeat Question 6 if \(\overline{A B}\) happens to be a diameter.
Answer:
Steps of construction :

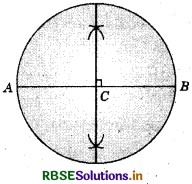
1. With centre C and radius’ 3.4 cm, draw a circles.   
2. Draw a diameter \(\overline{A B}\) of the circle.  
3. Draw the perpendicular bisector of \(\overline{A B}\). We find that it passes through the centre C of the circle.

Question 8.
Draw a circle of radius 4 cm. Draw any two of its chords. Construct the perpendicular bisectors of these chords, where do they meet?
Answer:
Steps of construction :
1. By taking 0 as centre, draw a circle of radius 4 cm.
2. Draw two chords AB and CD.

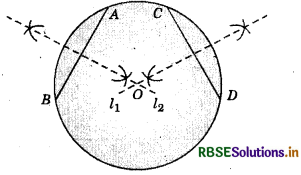
3. Draw the perpendicular bisector l₁ of \(\overline{A B}\).
4. Draw the perpendicular bisector L₂ of \(\overline{C D}\).
5. Produce l₁ and l₂ to meet each other. We find that l₁ and l₂ meet at point O, the centre of the circle.

Question 9.
Draw any angle wÏth vertex O. Take a point A on one of its arms and B on another such that OA = OB. Draw the perpendicular bisector of\( \overline{O A}\) and \(\overline{O B}\). Let them meet at P. Is PA = PB?
Answer:
Steps of construction:
1. Mark a point ‘O’ on the paper.
2. Draw an angle ∠XOY, having vertex O.

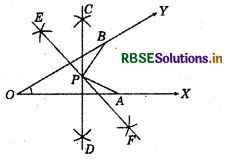
3. Open the compasses of fixed length, by taking O as centre cut two arcs at OX and OY named as A and B.
4. Now, draw the perpendicular bisector of OA and OB, let these intersect at point P. 
5. Join PA and PB.
6. By measuring them with the help of divider, we get, PA = PB.