RBSE Solutions for Class 6 Maths Chapter 12 Ratio and Proportion InText Questions

Rajasthan Board RBSE Solutions for Class 6 Maths Chapter 12 Ratio and Proportion InText Questions Textbook Exercise Questions and Answers.

RBSE Class 6 Maths Solutions Chapter 12 Ratio and Proportion InText Questions

(Try These Page No: 254)

Question 1. 
In a class, there are 20 boys and 40 girls. What is the ratio of the number of boys to the number of girls?
Answer:
Number of boys = 20 
Number of girls = 40 
Now, number of boys : number of girls
⇒ \(\frac{20}{40}=\frac{1}{2}\) = 1 : 2

Question 2. 
Ravi walks 6 km in an hour while Roshan walks 4 km in an hour. What is the ratio of the distance covered by Ravi to the distance covered by Roshan?
Answer: 
Distance, covered by Ravi: Distance covered by Roshan
6 : 4
⇒ \(\frac{6}{4}=\frac{3}{2}\) = 3 : 2
Hence, the distance covered by Ravi to the distance covered by Roshan is 3 : 2.

(Try These Page No: 246)

Question 1. 
Saurabh takes 15 minutes to reach school from his house and Sachin takes one hour to reach school from his house. Find the ratio of the time taken by Saurabh to the time taken by Sachin. 
Answer: 
Time taken by Saurabh = 15 minutes 
Also, time taken by Sachin = 1 hour = 60 minutes
Now, time taken by Saurabh : time taken by Sachin 15 : 60
⇒ \(\frac{15}{60}=\frac{1}{4}\) = 1 : 4

Question 2. 
Cost of a toffee is 50 paise and cost of a chocolate is ? 10. Find the ratio of the cost of a toffee to the cost of a chocolate.    .
Answer: 
Cost of a toffee = 50 paise 
Cost of a chocolate = ₹ 10
= 10 × 100 paise = 1000 paise
Now, cost of a toffee : cost of a chocolate = 50: 1000
⇒ \(\frac{50}{1000}=\frac{1}{20}\) = 1 : 20
Hence, ratio of the cost of a toffee to the cost of a chocolate is 1 : 20.

Question 3. 
In a school, there were 73 holidays in one year. What is the ratio of the number of holidays to the number of days in one year?
Answer:
Number of days in one year = 365 
Number of holidays in one year = 73 
Now, number of holidays : number of days 73: 365
⇒ \(\frac{73}{365}=\frac{1}{5}\) = 1 : 5
Hence, ratio of the number of holidays to the number of days in one year is 1 : 5.

(Try These Page No: 248)

Question 1. 
Find the ratio of number of notebooks to the number of books in your bag.
Answer:
Let, 8 notebooks and 6 books in the bag.
∴ Number of notebooks = 8
and Number of books = 6
∴ Ratio of number of notebooks to the
number of books = 8 : 6 = 4 : 3

Question 2.
Find the ratio of number of desks and chairs in your classroom.
Answer:
Let, 30 desk and 30 chairs in your classroom.    
∴ Number of desks = 30
and Number of chairs = 30
∴ Ratio of number of desks to the number of chairs = 30 : 30 = 1 : 1

Question 3. 
Find the number of students above twelve years of age in your class. Then, find the ratio of number of students with age above twelve years and the remaining students.
Answer:
Let, total students in your class = 40 
Number of students above 12 years = 10 
∴ Remaining students of below 12 years = 40 - 10 = 30 
∴ Ratio of number of students above twelve years and the remaining students = 10 : 30 = 1 : 3

Question 4. 
Find the ratio of number of doors and the number of windows in your classroom.
Answer:
Let 2 doors and 4 windows in your classroom.
∴ Number of doors = 2
and Number of windows = 4 
∴ Ratio of number of doors and the number of windows = 2 : 4 = 1 : 2

Question 5. 
Draw any rectangle and find the ratio of its length to its breadth.
Answer:
Let a rectangle ABCD and its dimensions are shown in figure :

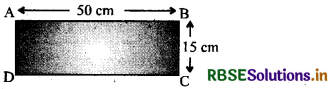
∴ Length = 50 cm and Breadth = 15 cm 
∴ Ratio of its length and breadth 
= 50 cm: 15 cm 
= 50: 15 = 10:3

(Try These Page No:254)

Question 1. 
Check whether the given ratios are equal, i.e. they are in proportion.
If yes, then write them in the proper form.
(i) 1:5 and 3:15 
(ii) 2:9 and 18:81 
(iii) 5:45 and 5:25 
(iv) 4:12 and 9:27 
(v) ₹ 10 to ₹ 15 and 4 to 6 
Answer: 
(i) Given ratios are 1: 5 and 3 : 15.
We have 3 : 15 = \(\frac{3}{15}=\frac{3 \div 3}{15 \div 3}\)
{∵ HCF of 3 and 15 is 3.}
i.    e. 1 : 5 and 3 : 15 are in proportion. 
Thus, the proper form is 1:5 :: 3:15.

(ii)    Given ratios are 2 : 9 and 18: 81.
We have 18 : 81 = \(\frac{18}{81}=\frac{18 \div 9}{81 \div 9}\)
{∵ HCF of 18 and 81 is 9.} 
= \(\frac{2}{9}\) = 2:9
i.e. 2 : 9 and 18 : 81 are in proportion. 
Thus, the proper form is 2 : 9 :: 18 : 81.

(iii)    Given ratios are 15 : 45 and 5 : 25.
We have 15 : 45 = \(\frac{15}{45}=\frac{15 \div 15}{45 \div 15}\)
{ ∵ HCF of 15 and 45 is 15.}
= \(\frac{1}{3}\) = 1 : 3
Again, we have 
5 : 25 = \(\frac{5}{25}=\frac{5 \div 5}{25 \div 5}\)
{∵ HCF of 5 and 25 is 5.}
= \(\frac{1}{5}\) = 1 : 5
∵ 1 : 3 ≠ 1 : 5
Therefore, 15 : 45 and 5 : 25 are not in proportion.

(iv)    Given ratios are 4 : 12 and 9 : 27.
We have, 4 : 12 = \(\frac{4}{12}=\frac{4 \div 4}{12 \div 4}\)
{∵ HCF of 4 and 12 is 4.}
= \(\frac{1}{3}\) = 1 : 3

Again, we have 
9 : 27 = \(\frac{9}{27}=\frac{9 \div 9}{27 \div 9}\)
{ ∵ HCF of 9 and 27 is 9.}
= \(\frac{1}{3}\) = 1 : 3
4 : 12 = 9 : 27
Thus, 4 : 12 and 9 : 27 are in proportion and the proper form is 4 : 12 : : 9 : 27.

(v) ₹  10 to ₹  15 and 4 to 6
We have ₹ 10 : ₹  15 = \(\frac{10}{15}=\frac{10 \div 5}{15 \div 5}\)
{ ∵ HCF of 10 and 15 is 5.}
= \(\frac{2}{3}\) = 2 : 3     
Also, we have 4 : 6 = \(\frac{4}{6}=\frac{4 \div 2}{6 \div 2}\)
{ ∵ HCF of 4 and 6 is 2.} 
= \(\frac{2}{3}\) = 2 : 3     
i.e. 10 : 15 and 4 : 6 are in proportion. 
Thus, the proper form is 10 : 15 :: 4: 6.

(Try These Page No: 257)

Question 1. 
Prepare five similar problems and ask your friends to solve them.
Answer:
Do it yourself.

Question 2. 
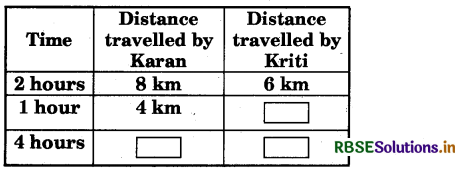
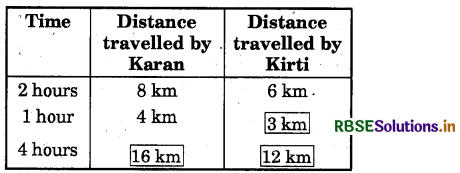
Read the table and fill in the blanks:

Answer: 
Distance travelled by Karan in an hour = 4 km
So, distance travelled by Karan in 4 hours = (4 × 4) km = 16 km
Again,    
∵ Distance travelled by Kriti in 2 hours = 6 km
∵ Distance travelled by Kriti in 1 hour 
= (6 + 2) km = 3 km
Distance travelled by Kriti in 4 hours = (3 × 4) km = 12 km