RBSE Solutions for Class 6 Maths Chapter 10 Mensuration Ex 10.3

Rajasthan Board RBSE Solutions for Class 6 Maths Chapter 10 Mensuration Ex 10.3 Textbook Exercise Questions and Answers.

RBSE Class 6 Maths Solutions Chapter 10 Mensuration Ex 10.3

Question 1.
Find the areas of the rectangles whose sides are :
(a) 3 cm and 4 cm
(b) 12 m and 21 m
(c) 2 km and 3 km
(d) 2 m and 70 cm
Answer:
(a) Here, Length = 3 cm
Breadth = 4 cm
Area of rectangle = length × breadth = 3 cm × 4 cm = 12 cm².

(b) Here, Length = 12 m
Breadth = 21 m
Area of rectangle = length × breadth = 12 m × 21 m = 252 m².

(c) Here, Length = 2 km
Breadth = 3 km
Area of rectangle = length × breadth = 2 km × 3 km = 6 km².

(d) Here, Length = 2 m
Breadth = 70 cm
Area of rectangle = length × breadth = 2 m × 0.7 m = 1.4 m².

Question 2.
Find the areas of the squares, whose sides are:
(a) 10 cm
(b) 14 cm
(c) 5 m
Answer:
(a) Side of square = 10 cm
∴ Area of square = (side)²
= (10)² = 100 cm².

(b) Side of square = 14 cm
∴ Area of square = (side)²
= (14)² = 196 cm².

(c) Side of square = 5 m
∴ Area of square = (side)²
= (5)² = 25 m².

Question 3.
The length and breadth of three rectangles are as given below :
(a) 9 m and 6 m
(b) 17 m and 3 m
(c) 4 m and 14 m
Which one has the largest area and which one has the smallest?
Answer:
(a) Length of rectangle = 9 m Breadth = 6 m
Area of rectangle = length × breadth = 9 m × 6 m = 54 m².

(b) Length = 17 m Breadth = 3 m
Area of rectangle = length × breadth
= 17 m × 3 m = 51 m².

(c) Length = 4 m Breadth = 14 m
Area of rectangle = length × breadth
= 4 m × 14 m = 56 m².
Hence, (c) has largest area and (b) has smallest area.

Question 4.
The area of a rectangular garden 50 m long is 300 sQuestion m. Find the width of the garden.
Answer:
Given that
Area of rectangular garden = 300 sq. m Length of the garden = 50 m
∵ Length × Breadth = 300 ⇒ 50 × Breadth = 300
⇒ Breadth = m = 6 m
Hence, breadth of rectangular garden is 6 m.

Question 5.
What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of ₹ 8 per hundred sq. m ?
Answer:
Length of rectangular plot = 500 m
Breadth of rectangular plot = 200 m
Area = length x breadth
= 500 mx 200 m= 100000 m2
∴ The cost of tiling at the rate of ₹ 8 per 100 sq. m
= ₹ \(\frac{8}{100}\) × 100000 = ₹ 8,000.

Question 6.
A table-top measures 2 m by 1 m 50 cm. What is its area in square metre?
Answer:
Length of table-top = 2 m
Breadth of table-top = 1 m 50 cm = 1.50 m
Area of the table-top = length × breadth
= 2 m × 1.50 m
= 3.0 sq. m.

Question 7.
A room is 4 m long and 3 m 50 cm wide. How many square metres of carpet is needed to cover the floor of the room?
Answer:
Length of the room= 4 m
Breadth of the room = 3 m 50 cm = 3.5 m
Area of carpet required to cover the floor
= length × breadth = 4m × 3.5 m = 14.0 sq. m
Hence, 14 sq. m of carpet is required to cover the floor of the room.

Question 8.
A floor is 5 m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.
Answer:
Length of the floor = 5 m
Breadth of the floor = 4 m
Area of the floor = length × breadth = 5 m × 4 m = 20 m²
Area of the square plot = side × side
= 3m × 3m = 9m²
∴ Area of the floor that is not carpeted
= 20 m² - 9 m² = 11 m².

Question 9.
Five square flower beds each of sides 1 m are dug on a piece of land 5 m long and 4 m wide. What is the area of the remaining part of the land?
Answer:
Area of square flower bed = side × side
= 1m × 1m = 1 m²

Area of 5 square flower beds
= 5 × 1 m² = 5 m²
Length of piece of land = 5 m
Breadth of piece of land = 4 m

∴ Area of the piece of land
= length × breadth = 5m × 4m = 20m²

∴ Area of the remaining part of the land
= 20 m² - 5 m² = 15 m²

Question 10.
By splitting the following figures into rectangles, find their areas (the measures are given in centimetre):

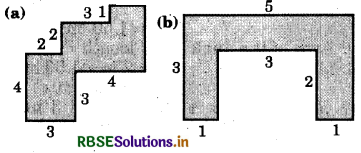
Answer:
(a) By dividing the figure in four parts named as (1), (2), (3) and (4), we have

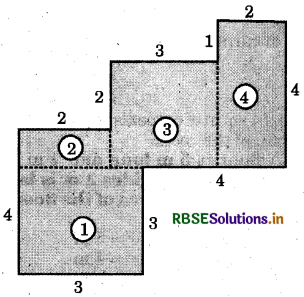
Area of part 1 = 3cm × 3cm = 9 cm²
Area of part 2 = 2 cm × 1 cm = 2 cm²
Area of part 3 = 3cm × 3cm = 9 cm²
Area of part 4 = 4cm × 2cm = 8 cm²

Area of the figure
= 9 cm² + 2 cm² + 9 cm² + 8 cm²
= 28 cm²

(b) Dividing the figure in three parts named as (1), (2) and (3), we have 5

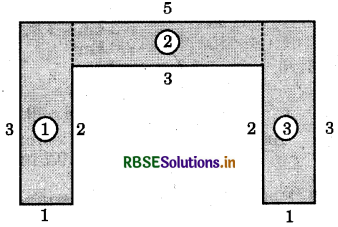
Area of part 1 = 3cm × 1cm = 3 cm²
Area of part 2 = 3cm × 1cm = 3 cm²
Area of part 3 = 3cm × 1cm = 3 cm²
Area of the figure = 3 cm² + 3 cm² + 3 cm² = 9 cm² .

Question 11.
Split the following shapes into rectangles and find their area. (The measures are given in centimetre) :

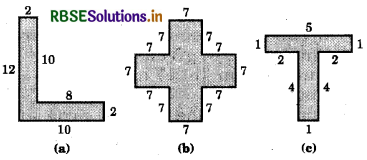
Answer:
(a) Dividing the figure in two parts named as (1) and (2)

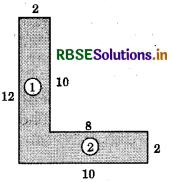
Area of the part 1 = 10 × 2 = 20 cm²
Area of the part 2 = 10 × 2 = 20 cm²
Total area = 20 cm² + 20 cm² = 40 cm².

(b) The following figure is divided into five squares of side 7 cm each.

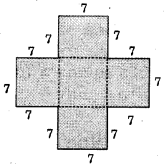
Area of figure = 5 × (area of each square)
= 5 × (7)² = 5 × 49 = 245 cm².

Area of the figure
= (5 × 1 + 4 × 1) cm²
= (5 + 4) cm²
= 9 cm².

c) Here, the figure is divided into two rectangles of dimensions 5 cm × 1 cm and 4 cm × 1 cm.

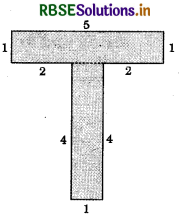
∴ Area of the figure
= (5 × 1 + 4 × 1) cm²
= (5 + 4) cm²
= 9 cm².

Question 12.
How many tiles whose length and breadth are 12 cm and 5 cm respectively will be needed to fit in a rectangular region whose length and breadth are respectively:
(a) 100 cm and 144 cm,
(b) 70 cm and 36 cm.
Answer:
(a) Length of rectangular region
= 100 cm
Breadth of the region = 144 cm
∴ Area of rectangular region
= length × breadth = 100 cm × 144 cm = 14400 cm²

Length of a tile = 12 cm
Breadth of a tile = 5 cm
∴ Area of a tile = length × breadth
= 12 cm × 5 cm = 60 cm²

∴ Number of tiles needed
= \(\frac{\text { Area of rectangular region }}{\text { Area of a tile }}\)
= \(\frac{14400 \mathrm{~cm}^{2}}{60 \mathrm{~cm}^{2}}\)
= 240 tugs,

(b) Length of the region = 70 cm
Breadth of the region = 36 cm
∴ Area of the rectangular region
= 70 cm × 36 cm
= 2520 cm²
Area of a tile = 60 cm²

∴ Number of tiles required to fit the region
= \(\frac{\text { Area of the rectangular region }}{\text { Area of a tile }}\)
= \(\frac{2520}{60}\) = 42 tiles.