RBSE Class 9 Maths Notes Chapter 6 रेखाएँ और कोण

These comprehensive RBSE Class 9 Maths Notes Chapter 6 रेखाएँ और कोण will give a brief overview of all the concepts.

RBSE Class 9 Maths Chapter 6 Notes रेखाएँ और कोण

→ कोण-कोई भी दो किरणें जिनका प्रारम्भिक बिन्दु एक ही हो, कोण बनाती हैं। बिन्दु या जिस बिन्दु पर रेखाएँ मिलती हैं उसे कोण या शीर्ष कहते हैं। कोण का माप तीन बिन्दुओं द्वारा लिखा जाता है। शीर्ष बिन्दु को बीच में रखा जाता है।

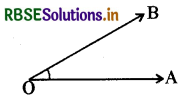
दिये गये चित्र में बिन्दु O से दो किरणें OA तथा OB निकलती हैं। यह आकृति कोण है। O को कोण का शीर्ष कहते हैं।

→ कोण की माप-ज्यामिति में कोण को नापने की इकाई डिग्री (Degree) है, यदि एक समकोण को 90 समान भागों में विभाजित किया जाये तो प्रत्येक भाग एक डिग्री का होता है। चूंकि एक समकोण को 90 बराबर भागों में बाँटा गया है।
अतः 1 समकोण = 90 डिग्री या 90°
प्रत्येक डिग्री को 60 समान भागों में बाँटने पर प्रत्येक भाग कला (मिनट) कहलाता है, इसी प्रकार प्रत्येक कला (मिनट) को 60 बराबर भागों में बाँटने पर प्रत्येक भाग एक विकला (सेकण्ड) कहलाता है।

→ कोण के प्रकार (कोणों का वर्गीकरण)
न्यून कोण (Acute Angle): वह कोण जो एक समकोण या 90° से छोटा हो, (0° से 90° के मध्य) न्यून कोण कहलाता है।

→ समकोण (Right Angle): 90° के कोण को समकोण कहते हैं।

→ अधिक कोण (Obtuse Angle): एक समकोण से बड़ा और दो समकोण से छोटा कोण, अधिक कोण कहलाता है।

→ ऋजु कोण या सरल कोण (Straight Angle): ऐसा कोण जो दो समकोण के बराबर हो, उसे ऋजु कोण कहते हैं।

→ वृहत् कोण (Reflex Angle): दो समकोण से बड़े एवं चार समकोण से छोटे कोण को वृहत् कोण कहते हैं।

→ आसन्न कोण (Adjacent Angles): ऐसे दो कोण जिनका शीर्ष तथा एक भुजा उभयनिष्ठ हो तथा जो उभयनिष्ठ भुजा के विपरीत ओर बने हों, आसन्न कोण कहलाते हैं।

→ सम्पूरक कोण (Supplementary Angles): जब दो कोणों का योग 2 समकोण के बराबर होता है तो प्रत्येक.कोण दूसरे कोण का सम्पूरक कोण कहलाता है।

→ पूरक कोण (Complementary Angles): जब दो कोणों का योग 1 समकोण के बराबर है तो वे एक-दूसरे के पूरक कोण कहलाते हैं।

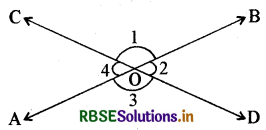
→ शीर्षाभिमुख कोण (Vertically Opposite Angles): संलग्न चित्र में सरल रेखा AB और CD एक-दूसरे को बिन्दु 0 पर काटती हैं और कोण ∠1, ∠2, ∠3 और ∠4 बनाती हैं। इनमें ∠1, ∠3 के सामने है और ∠2, ∠4 के सामने है। ऐसे कोणों को शीर्षाभिमुख कोण कहते हैं।

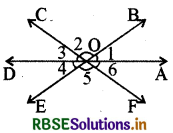
→ एक बिन्दु के चारों ओर बनने वाले कोण-यदि एक बिन्दु पर विभिन्न सरल रेखाएँ मिलें तो इस प्रकार बने कोणों को एक बिन्दु के चारों ओर बने कोण कहा जाता है। चित्र में अंकित कोण ∠1, ∠2, ∠3, ∠4, ∠5 व ∠6 एक ही बिन्दु O के चारों ओर बनने वाले कोण हैं। स्मरण रहे कि एक बिन्दु पर। बनने वाले समस्त कोणों का योग 360° होता है।

→ कोणों के रैखिक युग्म-दो आसन्न कोणों की जिनकी उभयनिष्ठ भुजा के अतिरिक्त भुजायें दो विपरीत किरणें हों, कोणों का रैखिक युग्म कहलाता है। (इनके कोणों का माप 180° होता है।)

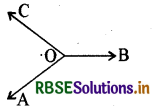
दो आसन्न कोण एक रैखिक कोण युग्म होते हैं यदि और केवल यदि वे सम्पूरक कोण हों।

→ प्रमेय 6.1. यदि दो सरल रेखाएँ परस्पर प्रतिच्छेद करें तो इस प्रकार बने शीर्षाभिमुख कोण बराबर होते हैं।।

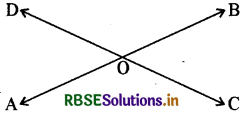
उपर्युक्त चित्र में, ∠COB = ∠AOD तथा ∠AOC = ∠BOD

→ उपप्रमेय-यदि दो सरल रेखाएँ एक-दूसरे को प्रतिच्छेद करें तो प्रतिच्छेद बिन्दु पर बनने वाले सभी | कोणों का योगफल 360° के बराबर होता है।

→ उपप्रमेय-शीर्षाभिमुख कोणों के अर्द्धक एक सरल रेखा में होते हैं।

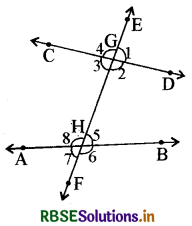
दो रेखाओं के साथ तिर्यक रेखा द्वारा बनाये गए कोण-ऐसी सरल रेखा को जो दो या अधिक सरल रेखाओं को अलग-अलग बिन्दुओं पर काटे, उनको तिर्यक रेखा कहते हैं। यहाँ चित्र में रेखा EF एक तिर्यक रेखा है।
यहाँ आकृति में ये तीन रेखाएँ AB, CD व EF कुल आठ कोण बनाती हैं। बिन्दु G पर चार कोण ∠1, ∠2, ∠3 एवं ∠4 बन रहे हैं। बिन्दु न पर भी चार कोण ∠5, ∠6, ∠7 एवं ∠8 बन रहे हैं। इनके नाम इनकी स्थिति के अनुसार दिये गए हैं।

→ संगत कोण (Corresponding Angles): निम्न प्रकार के कोण युग्म संगत कोण कहलाते हैं

• ∠1 तथा ∠5
• ∠2 तथा ∠6
• ∠4 तथा ∠8
• ∠3 तथा ∠7

स्पष्ट है कि संगत कोण तिर्यक रेखा (transversal) के एक ही ओर स्थित होते हैं और कोणों की स्थिति एक जैसी होती है।

→ एकान्तर कोण (Alternate Angles): निम्न प्रकार के कोण युग्म एकान्तर कोण कहलाते हैं

• ∠3 तथा ∠5
• ∠2 तथा ∠8 एकान्तर कोण, तिर्यक रेखा के विपरीत ओर स्थित होते हैं।

→ अन्तःकोण (Interior Angles): निम्न प्रकार के कोण युग्म, अन्त:कोण कहलाते हैं

• ∠2 तथा ∠5
• ∠3 तथा ∠8

अन्तःकोण, तिर्यक रेखा के एक ही ओर स्थित होते हैं।

→ बहिष्कोण (Exterior Angles): आकृति में दर्शाये गए कोण ∠1, ∠4, ∠6 एवं ∠7 बहिष्कोण कहलाते हैं। सामान्यतः उपर्युक्त कोण युग्मों के मध्य कोई सम्बन्ध नहीं होता है, परन्तु यदि दो या अधिक समान्तर रेखाओं को एक तिर्यक रेखा काटे तो

• संगत कोण बराबर होते हैं।
• एकान्तर कोण बराबर होते हैं।
• अन्तःकोण सम्पूरक होते हैं। उपर्युक्त कथनों के विलोम भी सत्य होते हैं।

→ प्रमेय 6.2. यदि दो समान्तर रेखाओं को एक तिर्यक रेखा काटे तो इस प्रकार बने एकान्तर कोण बराबर होते हैं।

→ प्रमेय 6.3. (प्रमेय 6.2 का विलोम)-यदि दो सरल रेखाओं को एक तिर्यक रेखा काटे तो इस प्रकार बने एकान्तर कोणों का कोई भी एक जोड़ा बराबर हो, तो वे रेखाएँ समान्तर होती हैं।

→ प्रमेय 6.4. यदि दो समान्तर रेखाओं को कोई एक तिर्यक रेखा काटे तो एक ओर के अन्तःकोणों का योग 2 समकोण होता है।

→ प्रमेय 6.5. ( प्रमेय 6.4 का विलोम)-यदि दो सरल रेखाओं को कोई तिर्यक रेखा काटे और इस प्रकार बनने वाले अन्तःकोणों के किसी एक जोड़े का योग 180° या 2 समकोण हो तो दोनों रेखाएँ समान्तर होती हैं।

→ उपप्रमेय-एक ही रेखा पर खींचे गये लम्ब परस्पर समान्तर होते हैं।

→ यदि एक किरण एक रेखा पर खड़ी हो, तो इस प्रकार बने दोनों आसन्न कोणों का योग 180° होता है और विलोमतः यदि दो आसन्न कोणों का योग 180° है तो उनकी उभयनिष्ठ भुजाएँ एक रेखा बनाती हैं। इन गुणों को मिलाकर रैखिक युग्म अभिगृहीत कहते हैं।

→ यदि एक तिर्यक रेखा दो समान्तर रेखाओं को प्रतिच्छेद करे तो

• संगत कोणों का प्रत्येक युग्म बराबर होता है।
• एकान्तर अंत:कोणों का प्रत्येक युग्म बराबर होता है।
• तिर्यक रेखा के एक ही ओर के अंत:कोणों का प्रत्येक युग्म संपूरक होता है।

→ यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार प्रतिच्छेदित करे कि या तो

• संगत कोणों का कोई एक युग्म बराबर हो या
• एकान्तर अंत:कोणों का कोई एक युग्म बराबर हो या
• तिर्यक रेखा के एक ही ओर के अंत:कोणों का कोई एक युग्म संपूरक हो, तो ये दोनों रेखाएँ समान्तर होती हैं।

→ वे रेखाएँ जो एक ही रेखा के समान्तर होती हैं, परस्पर समान्तर होती हैं।

→ एक त्रिभुज के तीनों कोणों का योग 180° होता है।

→ यदि किसी त्रिभुज की एक भुजा को बढ़ाया जाये, तो इस प्रकार बना बहिष्कोण अपने दोनों अंत:अभिमुख कोणों के योग के बराबर होता है।