RBSE Class 9 Maths Notes Chapter 12 हीरोन सूत्र

These comprehensive RBSE Class 9 Maths Notes Chapter 12 हीरोन सूत्र will give a brief overview of all the concepts.

RBSE Class 9 Maths Chapter 12 Notes हीरोन सूत्र

→ त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) × आधार × ऊँचाई

→ त्रिभुज का आधार

→ त्रिभुज की ऊँचाई

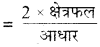
→ यदि किसी त्रिभुज की भुजाएँ a, b और c हों, तो हीरोन के सूत्र द्वारा त्रिभुज का क्षेत्रफल \(\sqrt{s(s-a)(s-b)(s-c)}\) होता है जहाँ s = \(\frac{a+b+c}{2}\) है। यहाँ s त्रिभुज का अर्द्ध-परिमाप कहलाता है।

→ समद्विबाहु त्रिभुज का क्षेत्रफल = \(\frac{b}{4} \sqrt{4 a^{2}-b^{2}}\) वर्ग इकाई यहाँ पर समद्विबाहु त्रिभुज की दो समान भुजाओं की लम्बाई a एवं तीसरी भुजा की लम्बाई b है।

→ समबाहु त्रिभुज का अर्द्धपरिमाप = \(\frac{3 a}{2}\)

→ समबाहु त्रिभुज का क्षेत्रफल = \(\frac{a^{2} \sqrt{3}}{4}\) वर्ग इकाई

→ समकोण त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) × a × b
= \(\frac{1}{2}\) × (समकोण वाली भुजाओं का गुणनफल)

→ एक चतुर्भुज जिसकी भुजाएँ तथा एक विकर्ण दिये हों, तो उसका क्षेत्रफल उसे दो त्रिभुजों में विभाजित | करके और फिर हीरोन के सूत्र का प्रयोग करके ज्ञात किया जा सकता है।