RBSE Class 9 Maths Notes Chapter 10 वृत्त

These comprehensive RBSE Class 9 Maths Notes Chapter 10 वृत्त will give a brief overview of all the concepts.

RBSE Class 9 Maths Chapter 10 Notes वृत्त

→ वृत्त : वृत्त एक समतल में स्थित उन बिन्दुओं का समुच्चय होता है जो उस समतल में दिए गए स्थिर बिन्दु से नियत दूरी पर होते हैं। वह वृत्त जिसका केन्द्र 0 तथा त्रिज्या r हो तो सामान्यत: C (O, r) द्वारा व्यक्त करते हैं।

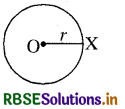
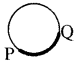
→ वृत्त का चाप : वृत्त का एक सतत भाग उस वृत्त का चाप कहलाता है। चाप PQ को \(\widehat{\mathrm{PQ}}\) से व्यक्त करते हैं।

→ केन्द्रीय कोण : जिस कोण का शीर्ष वृत्त का केन्द्र हो उसे केन्द्रीय कोण कहते हैं।

→ चाप का डिग्री माप: चाप \(\widehat{\mathrm{AB}}\) द्वारा वृत्त के केन्द्र पर अन्तरित कोण ∠AOB के माप को उस चाप का अंश माप या डिग्री माप कहते हैं।

→ लघु चाप, दीर्घ चाप: लघु चाप का डिग्री माप 180° से कम होता है, दीर्घ चाप का डिग्री माप 180° से अधिक होता है जबकि अर्द्धवृत्त का डिग्री माप 180° के बराबर होता है।

→ वृत्त की जीवा: वृत्त के दो बिन्दुओं के मिलाने वाले रेखाखण्ड को वृत्त की जीवा कहते हैं।

→ वृत्त का व्यास: वृत्त के केन्द्र से होकर जाने वाली जीवा को वृत्त का व्यास कहते हैं। किसी वृत्त के अनेक व्यास हो सकते हैं तथा व्यास उस वृत्त की सबसे लम्बी जीवा होती है।

→ अर्द्ध वृत्त: किसी भी वृत्त का व्यास, उस वृत्त को दो बराबर लम्बाई के चापों में बाँटता है। इनमें से प्रत्येक चाप, 'अर्द्धवृत्त' कहलाता है।

→ वृत्त खण्ड: जीवा वृत्त के घिरे क्षेत्र अर्थात् वृत्ताकार चकती को दो भागों में विभाजित करती है। इन भागों में से प्रत्येक भाग को वृत्त खण्ड कहते हैं।

→ त्रिज्यखण्ड: वृत्त का त्रिज्यखण्ड वह भाग होता है जो एक चाप तथा इसके सिरों को केन्द्र से मिलाने वाली त्रिज्याओं के बीच होता है।

→ एकान्तर वृत्त खण्ड: किसी जीवा द्वारा लघु तथा दीर्घ वृत्त खण्ड एक-दूसरे के एकान्तर वृत्त खण्ड कहलाते हैं।

→ एक वृत्त (या सर्वांगसम वृत्त) की समान जीवायें केन्द्र पर समान कोण बनाती हैं।

→ सर्वांगसम वृत्तों (या एक ही वृत्त) में दो चाप बराबर हों तो उनकी संगत जीवाएँ समान लम्बाई की होती हैं।

→ सर्वांगसम वृत्तों (या एक ही वृत्त) में दो जीवाएँ बराबर हों तो उनके संगत चाप परस्पर सर्वांगसम होते है

→ वृत्त के केन्द्र से जीवा पर डाला गया लम्ब उस जीवा को समद्विभाजित करता है।

→ वृत्त के केन्द्र और जीवा के मध्य बिन्दु को मिलाने वाली रेखा जीवा पर लम्ब होती है।

→ तीन असरेख बिन्दुओं से होकर एक और केवल एक ही वृत्त गुजर सकता है।

→ सर्वांगसम वृत्तों (या एक ही वृत्त) में समान जीवाएँ संगत केन्द्र से समदूरस्थ होती हैं।

→ किसी वृत्त की जीवाएँ जो वृत्त के केन्द्र से बराबर दूरी पर हैं, परस्पर बराबर होती हैं।

→ वृत्त की जीवाएँ जो केन्द्र से समदूरस्थ हैं, लम्बाई में बराबर होती हैं।

→ किसी वृत्त की सर्वांगसम चाप केन्द्र पर बराबर कोण अंतरित करते हैं।

→ वृत्त के किसी चाप द्वारा वृत्त के केन्द्र पर अन्तरित कोण उसी चाप द्वारा वृत्त के शेष भाग के किसी बिन्दु पर अन्तरित कोण का दुगुना होता है।

→ एक अर्द्धवृत्त में बना कोण समकोण होता है।

→ एक वृत्त का वह चाप जो वृत्त के शेष भाग पर समकोण अन्तरित करता है, एक अर्द्धवृत्त होता है।

→ वृत्त के एक ही वृत्तखण्ड में स्थित कोण समान होते हैं।

→ यदि दो बिन्दुओं को मिलाने वाले रेखाखण्ड उस रेखा, जिसमें रेखाखण्ड स्थित हैं, के एक ही ओर स्थित अन्य दो बिन्दुओं पर समान कोण अन्तरित करता हो, ये चारों बिन्दु एक वृत्तीय होते हैं।

→ वृत्त की समान जीवा केन्द्र पर समान कोण अन्तरित करती हैं।

→ सर्वांगसम वृत्तों की समान जीवायें संगत केन्द्रों पर समान कोण अन्तरित करती हैं।

→ यदि वृत्त की दो जीवायें केन्द्र पर समान कोण अन्तरित करती हैं, तो जीवायें समान होती हैं।

→ चतुर्भुज जिसमें सभी शीर्ष एक वृत्त पर स्थित हों, चक्रीय चतुर्भुज कहलाता है।

→ चक्रीय चतुर्भुज के सम्मुख कोणों के किसी भी युग्म का योग 180° होता है। इस प्रमेय को हम निम्न रूप में भी लिख सकते हैं "एक चक्रीय चतुर्भुज के सम्मुख सम्पूरक होते हैं।"

→ यदि चतुर्भुज के सम्मुख कोणों का एक युग्म सम्पूरक हो, तो चतुर्भुज चक्रीय होता है। 

→ यदि किसी चक्रीय चतुर्भुज की एक भुजा बढ़ाई जाए तो इस प्रकार अन्तरित बहिष्कोण अन्तराभिमुख कोण के बराबर होता है।

→ यदि एक चक्रीय चतुर्भुज के विकर्ण उसके शीर्षों से जाने वाले वृत्त के व्यास हों तो वह एक आयत होता है।

→ एक चक्रीय समान्तर चतुर्भुज एक आयत होता है।