RBSE Class 9 Maths Notes Chapter 1 संख्या पद्धति

These comprehensive RBSE Class 9 Maths Notes Chapter 1 संख्या पद्धति will give a brief overview of all the concepts.

RBSE Class 9 Maths Chapter 1 Notes संख्या पद्धति

→ संख्याओं 1, 2, 3, ...... ∞ (अनन्त) तक, जो कि प्राकृत संख्याएँ होती हैं, को N से प्रदर्शित किया जाता हैं।

→ यदि प्राकृत संख्याओं 1, 2, 3, ..... ∞ (अनन्त) तक में शून्य भी मिला दिया जाये अर्थात् 0, 1, 2, 3, ....... (अनन्त) हो तो इन्हें पूर्ण संख्याएँ (W) कहते हैं।

→ यदि पूर्ण संख्याओं के संग्रह में ऋणात्मक संख्याएँ भी सम्मिलित हों, अर्थात् ..... - 3, - 2, - 1, 0, 1, 2, 3, ...... तो यह नया संग्रह पूर्णांकों का संग्रह कहलाएगा जिसे Z से लिखते हैं।

→ समस्त ऐसी संख्याएँ जिनमें अंश व हर हो अर्थात् \(\frac{1}{2}, \frac{3}{4}, \frac{-2005}{2006}\) आदि प्रकार की संख्याएँ परिमेय संख्याओं का संग्रह कहलाता है। परिमेय संख्याओं का संग्रह Q के द्वारा प्रदर्शित किया जाता है।

→ संख्या को परिमेय संख्या कहा जाता है, यदि इसे \(\frac{p}{q}\) के रूप में लिखा जा सकता हो, यहाँ p और q पूर्णांक हैं तथा q ≠ 0 है।

→ परिमेय संख्या धनात्मक, ऋणात्मक अथवा शून्य हो सकती है। परिमेय संख्या \(\frac{p}{q}\) धनात्मक होती है, यदि p तथा q के समान चिह्न हों तथा वे ऋणात्मक होती हैं, यदि उनके चिह्न विपरीत हों।

→ प्रत्येक पूर्णांक एक परिमेय संख्या होती है परन्तु प्रत्येक परिमेय संख्या एक पूर्णांक हो, यह सत्य नहीं है। एक परिमेय संख्या का दशमलव प्रसार या तो सांत दशमलव होता है या अनवसानी (असांत) आवर्ती होता है।

→ प्रत्येक प्राकृत संख्या, प्रत्येक पूर्णांक तथा प्रत्येक भिन्न संख्या परिमेय संख्या होती है। शून्य (0) भी एक परिमेय संख्या है।

→ यदि किसी परिमेय संख्या के अंश और हर को समान संख्या में गुणा या भाग किया जाए तो परिमेय संख्या का मान नहीं बदलता है।

→ दो संख्याओं के मध्य परिमेय संख्या ज्ञात करना-

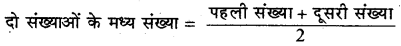
→ संख्या s को अपरिमेय संख्या कहा जाता है, यदि इसे \(\frac{p}{q}\) के रूप में न लिखा जा सकता हो, जहाँ p और q पूर्णांक हैं तथा q ≠ 0 है।

→ किन्हीं दो दी गई परिमेय संख्याओं के मध्य अपरिमित रूप से अनेक परिमेय संख्याएँ होती हैं।

→ एक परिमेय संख्या का दशमलव प्रसार या तो सांत होता है या अनवसानी आवर्ती होता है। साथ ही वह संख्या, जिसका दशमलव प्रसार सांत या अनवसानी आवर्ती है, परिमेय होती है।

→ एक अपरिमेय संख्या का दशमलव प्रसार अनवसानी अनावी होता है। साथ ही वह संख्या, जिसका दशमलव प्रसार अनवसानी अनावर्ती है, अपरिमेय होती है।

→ सांत दशमलव संख्या-जब किसी परिमेय संख्या का हर 2 या 5 या दोनों की घात में हो तो ऐसी परिमेय संख्याओं से सात दशमलव प्राप्त होता है। अर्थात् जब किसी परिमेय संख्या को भाग विधि से दशमलव में बदलने के लिए अंश में हर का भाग देने पर कुछ चरणों के बाद शेषफल शून्य प्राप्त हो जाता है तो वह संख्या सांत दशमलव कहलाती है।

→ असांत दशमलव या अनवसानी आवर्ती संख्या-जब किसी परिमेय संख्या के मानक रूप के हर में समय भाग क्रिया यदि निरन्तर चलती रहे या कुछ न कुछ शेषफल आता रहे, तो वह संख्या असांत दशमलव या अनवसानी आवर्ती संख्या कहलाती है।

→ एक संख्या जो परिमेय संख्या नहीं है, अपरिमेय संख्या कहलाती है। या एक ऐसी संख्या जिसे \(\frac{p}{q}\), (जहाँ p और q पूर्णांक हैं और q ≠ 0 के रूप में व्यक्त नहीं किया जा सकता, अपरिमेय संख्याएँ कहलाती हैं, जैसे √2, √3, √5 आदि अपरिमेय संख्याएँ हैं।

→ एक संख्या अपरिमेय संख्या होती है, यदि इसका दशमलव प्रसार या निरूपण अनवसानी अनावर्ती होता है। जैसे और अनवसानी अनावर्ती दशमलव हैं अतः 7 और e अपरिमेय संख्याएँ हैं।

→ समस्त परिमेय और अपरिमेय संख्याओं को एक साथ लेने पर वास्तविक संख्याओं का संग्रह प्राप्त होता है। प्रत्येक वास्तविक संख्या को संख्या रेखा के एक अद्वितीय बिन्दु से निरूपित किया जाता है। साथ ही, संख्या रेखा का प्रत्येक बिन्दु एक अद्वितीय वास्तविक संख्या को निरूपित करता है। इसी कारण संख्या रेखा को वास्तविक संख्या रेखा कहा जाता है।

→ प्रत्येक वास्तविक संख्या को संख्या रेखा के एक अद्वितीय बिन्दु से निरूपित किया जाता है। साथ ही संख्या रेखा का प्रत्येक बिन्दु एक अद्वितीय वास्तविक संख्या को निरूपित करता है। यही कारण है कि संख्या रेखा को वास्तविक संख्या रेखा कहा जाता है।

→ संख्या रेखा के प्रत्येक बिन्दु के संगत एक अद्वितीय वास्तविक संख्या होती है। साथ ही, प्रत्येक वास्तविक संख्या के संगत संख्या रेखा पर एक बिन्दु होता है।

→ किसी वास्तविक संख्या a के लिए,
|a| = a यदि a ≥ 0 और
|a| = - a यदि a < 0
|a|, संख्या a का निरपेक्ष मान कहलाता है।

→ |a| = |- a| = a जब तक a एक धनात्मक वास्तविक संख्या है।

→ यदि r परिमेय है और 5 अपरिमेय है, तब r + s और r - s अपरिमेय संख्याएँ होती हैं तथा rs और \(\frac{r}{s}\) अपरिमेय संख्याएँ होती हैं यदि r ≠ 0 हो।

→ यदि a तथा b दो परिमेय संख्याएँ हों जो कि पूर्ण वर्ग नहीं हैं, तो अपरिमेय संख्याएँ √a + √b और √a - √b एक-दूसरे के संयुग्मी कहलाते हैं। तथा

• दो संयुग्मी अपरिमेय संख्याओं का गुणनफल सदैव एक परिमेय संख्या होती है।
• द्विपदी द्विघाती अपरिमेय संख्या का सरलतम परिमेयकरण गुणनखण्ड इसका संयुग्मी होता है।

→ धनात्मकं वास्तविक संख्याओं a और b के सम्बन्ध में निम्नलिखित सर्वसमिकाएँ लागू होती हैं

• \(\sqrt{ab}\) = √a√b
• \(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\)
• (√a + √b) (√a - √b) = a - b
• (a + √b)(a - √b) = a² - b²
• (√a + √b) = a + 2\(\sqrt{ab}\) + b

→ \(\frac{1}{\sqrt{a}+b}\) के हर का परिमेयीकरण करने के लिए इसे हम \(\frac{\sqrt{a}-b}{\sqrt{a}-b}\) से गुणा करते हैं, जहाँ a और b पूर्णांक हैं।

→ मान लीजिए a > 0 एक वास्तविक संख्या है और p और q परिमेय संख्याएँ हैं, तब

• a^p.a^q = a^p+q
• (a^p)^q = a^pq
• \(\frac{a^{p}}{a^{q}}\) = a^p-q
• a^p. b^p = (ab)^p