RBSE Class 9 Maths Important Questions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल

Rajasthan Board RBSE Class 9 Maths Important Questions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Important Questions and Answers.

RBSE Class 9 Maths Chapter 9 Important Questions समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
यदि समान्तर चतुर्भुज का आधार 4 सेमी. व ऊँचाई 2 सेमी. हो तो क्षेत्रफल होगा-
(A) 8 सेमी.²
(B) 2 सेमी.²
(C) 16 सेमी.²
(D) 6 सेमी.²
उत्तरः
(A) 8 सेमी.²

प्रश्न 2.
यदि समान्तर चतुर्भुज की ऊँचाई 10 मी. व क्षेत्रफल 120 मी. है तो समान्तर चतुर्भुज का आधार होगा
(A) 10 मी.
(B) 12 मी.
(C) 1.2 मी.
(D) 20 मी.
उत्तरः
(B) 12 मी.

प्रश्न 3.
त्रिभुज के क्षेत्रफल का सूत्र है
(A) \(\frac{1}{2}\) × आधार × ऊँचाई
(B) \(\frac{1}{2}\) × [आधार + ऊँचाई]
(C) [आधार + ऊँचाई]
(D)

उत्तरः
(A) \(\frac{1}{2}\) × आधार × ऊँचाई

प्रश्न 4.
यदि त्रिभुज का आधार 20 सेमी. व ऊँचाई 10 सेमी. हो तो क्षेत्रफल होगा-
(A) 200 सेमी.²
(B) 30 सेमी.²
(C) 100 सेमी.²
(D) 50 सेमी.²
उत्तरः
(C) 100 सेमी.²

प्रश्न 5.
समलम्ब चतुर्भुज का क्षेत्रफल होता है-.
(A) \(\frac{1}{2}\) × ऊँचाई × (समान्तर भुजाओं का योग)
(B) \(\frac{1}{2}\) × ऊँचाई × (भुजा)
(C) \(\frac{1}{2}\) × आधार × ऊँचाई
(D) 2 × ऊँचाई × समान्तर भुजाओं का गुणा
उत्तरः
(A) \(\frac{1}{2}\) × ऊँचाई × (समान्तर भुजाओं का योग)

प्रश्न 6.
एक ही आधार व एक ही समान्तर रेखाओं के मध्य स्थित दो त्रिभुजों के क्षेत्रफल में सम्बन्ध है
(A) पहले त्रिभुज का क्षेत्रफल > दूसरे त्रिभुज का क्षेत्रफल
(B) पहले त्रिभुज का क्षेत्रफल < दूसरे त्रिभुज का क्षेत्रफल
(C) पहले त्रिभुज का क्षेत्रफल = दूसरे त्रिभुज का क्षेत्रफल
(D) पहले त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) दूसरे त्रिभुज का क्षेत्रफल
उत्तरः
(C) पहले त्रिभुज का क्षेत्रफल = दूसरे त्रिभुज का क्षेत्रफल

प्रश्न 7.
एक आयत व एक समान्तर चतुर्भुज एक ही आधार व एक ही समान्तर रेखाओं के मध्य स्थित हैं। यदि समान्तर चतुर्भुज का क्षेत्रफल 64 सेमी. हो व आयत की ऊँचाई 8 सेमी. हो तो आयत का आधार होगा
(A) 8 सेमी.
(B) 6.4 सेमी.
(C) 6 सेमी.
(D) 3 सेमी.
उत्तरः
(A) 8 सेमी.

प्रश्न 8.
समान्तर चतुर्भुज का क्षेत्रफल ज्ञात करने का सूत्र
(A) समान्तर चतुर्भुज का क्षेत्रफल = \(\frac{1}{2}\) × समान्तर चतुर्भुज की दोनों आसन्न भुजाओं का गुणा
(B) समान्तर चतुर्भुज का क्षेत्रफल = \(\frac{1}{2}\) × आधार × ऊँचाई
(C) समान्तर चतुर्भुज का क्षेत्रफल = समान्तर चतुर्भुज की दोनों आसन्न भुजाओं का गुणा
(D) समान्तर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई
उत्तरः
(D) समान्तर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई

प्रश्न 9.
त्रिभुज का क्षेत्रफल, इसकी भुजा और संगत शीर्ष लम्ब के गुणनफल का होता है
(A) बराबर
(B) आधा
(C) दुगुना
(D) चार गुना
उत्तरः
(B) आधा

प्रश्न 10.
यदि किसी समान्तर चतुर्भुज में AB = 14 cm., भुजाओं AB तथा AD के संगत शीर्षलम्ब 8 cm. और 7 cm. हैं तो AD का मान होगा
(A) 16 cm.
(B) 18 cm.
(C) 20 cm.
(D) 24 cm.
उत्तरः
(A) 16 cm.

प्रश्न 11.
दो समान्तर चतुर्भुज समान आधार एवं समान समान्तर रेखाओं के मध्य बने हुए हैं। इन समान्तर चतुर्भुजों के क्षेत्रफलों का अनुपात है
(A) 1 : 2
(B) 2 : 1
(C) 1 : 1
(D) 3 : 1
उत्तरः
(C) 1 : 1

प्रश्न 12.
माना ∆ABC का क्षेत्रफल 24 वर्ग सेमी. है और ∆ABC की भुजाओं के मध्य बिन्दुओं को मिलाने पर ∆PQR बनता है। तब ∆PQR का क्षेत्रफल है
(A) 12 वर्ग इकाई
(B) 6 वर्ग इकाई
(C) 4 वर्ग इकाई
(D) 3 वर्ग इकाई
उत्तरः
(B) 6 वर्ग इकाई

प्रश्न 13.
किसी त्रिभुज की माध्यिका इसे दो भागों में बाँटती है। वे दोनों भाग हैं
(A) सर्वांगसम त्रिभुज
(B) समद्विबाहु त्रिभुज
(C) समकोण त्रिभुज
(D) समान क्षेत्रफल वाले त्रिभुज
उत्तरः
(C) समकोण त्रिभुज

प्रश्न 14.
किसी समचतुर्भुज की आसन्न भुजाओं के मध्य बिन्दुओं को मिलाने पर बनने वाली आकृति का क्षेत्रफल क्या होगा यदि समचतुर्भुज के विकर्ण 16 सेमी. व 12 सेमी. लम्बाई के हैं-
(A) 28 सेमी.²
(B) 48 सेमी.²
(C) 96 सेमी.²
(D) 24 सेमी.²
उत्तरः
(B) 48 सेमी.²

प्रश्न 15.
किसी समान्तर चतुर्भुज PQRS के मध्य-बिन्दु ABCD हैं। यदि क्षेत्रफल (PQRS) = 36 सेमी.² तब क्षेत्रफल (ABCD) =
(A) 24 सेमी.
(B) 18 सेमी.
(C) 30 सेमी.
(D) 36 सेमी.
उत्तरः
(B) 18 सेमी.

प्रश्न 16.
यदि AD, ∆ABC की माध्यिका है और P, AC पर कोई बिन्दु है तब क्षेत्रफल (ADP) : क्षेत्रफल (ABD) = 2 : 3, तब क्षेत्रफल (∆PDC) : क्षेत्रफल (∆ABC) है-
(A) 1 : 5
(B) 5 : 1
(C) 1 : 6
(D) 3 : 5
उत्तरः
(C) 1 : 6

प्रश्न 17.
किसी आयत की आसन्न भुजाओं के मध्य बिन्दुओं को मिलाने पर बनने वाली आकृति, जबकि आयत की भुजाएँ 8 सेमी. व 6 सेमी. की हैं, होगी
(A) 24 सेमी. क्षेत्रफल वाला समचतुर्भुज
(B) 24 सेमी. क्षेत्रफल वाला आयत
(C) 26 सेमी. क्षेत्रफल वाला वर्ग
(D) 14 सेमी.
उत्तरः
(A) 24 सेमी. क्षेत्रफल वाला समचतुर्भुज

प्रश्न 18.
क्षेत्रफल वाला समलम्ब चतुर्भुज 18. किसी त्रिभुज ABC की माध्यिकाएँ G पर मिलती हैं। यदि क्षेत्रफल (∆ABC) = 27 सेमी. तब क्षेत्रफल (∆BGC) =
(A) 6 सेमी.²
(B) 9 सेमी.²
(C) 12 सेमी.²
(D) 18 सेमी.²
उत्तरः
(B) 9 सेमी.²

प्रश्न 19.
चित्र में, ABCD एक समान्तर चतुर्भुज है। यदि AB = 12 सेमी., AE = 7.5 सेमी., CF = 15 सेमी. तब AD =

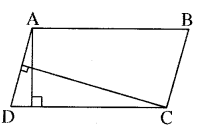
(A) 3 सेमी.
(B) 6 सेमी.
(C) 8 सेमी.
(D) 10.5 सेमी.
उत्तरः
(B) 6 सेमी.

प्रश्न 20.
यदि समलम्ब चतुर्भुज ABCD जिसमें AB || DC के विकर्ण AC और BD O पर एक-दूसरे को प्रतिच्छेदित करती हैं। वह त्रिभुज, जिसका क्षेत्रफल ∆AOD के बराबर है-
(A) ∆AOB
(B) ∆BOC
(C) ∆DOC
(D) ∆ADC
उत्तरः
(B) ∆BOC

प्रश्न 21.
ABCD एक समलम्ब चतुर्भुज है जिसमें AB || DC है। यदि क्षेत्रफल (∆ABD) = 24 सेमी.2 और AB = 8 सेमी., तब ∆ABC की ऊँचाई है-
(A) 3 सेमी.
(B) 4 सेमी.
(C) 6 सेमी.
(D) 8 सेमी.
उत्तरः
(C) 6 सेमी.

प्रश्न 22.
ABCD एक आयत है जिसमें 0, कोई बिन्दु इसके अन्दर है। यदि क्षेत्रफल (∆AOD) = 3 सेमी. और क्षेत्रफल (∆BOC) = 6 सेमी., तब आयत ABCD का क्षेत्रफल है
(A) 9 सेमी.²
(B) 12 सेमी.²
(C) 15 सेमी.²
(D) 18 सेमी.²
उत्तरः
(D) 18 सेमी.²

प्रश्न 23.
ABCD एक समलम्ब चतुर्भुज है जिसकी समान्तर भुजाएँ AB = a तथा DC = b हैं। यदि E एवं F क्रमशः असमान्तर भुजाओं AD और BC के मध्य बिन्दु हैं तब चतुर्भुज ABFE और EFCD के क्षेत्रफलों का अनुपात है
(A) a : b
(B) (a + 3b) : (3a + b)
(C) (3a + b) : (a + 3b)
(D) (2a + b) : (3a + b)
उत्तरः
(C) (3a + b) : (a + 3b)

प्रश्न 24.
चित्र में, PQRS एक समान्तर चतुर्भुज है। यदि X और Y क्रमशः PQ और SR के मध्य-बिन्दु हैं और विकर्ण SQ को मिलाते हैं। तब ar(समान्तर चतुर्भुज XQRY) : ar(∆QSR) =

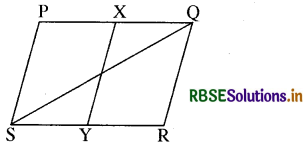
(A) 1 : 4
(B) 2 : 1
(C) 1 : 2
(D) 1 : 1
उत्तरः
(D) 1 : 1

प्रश्न 25.
चित्र में, ABCD और FECG समान क्षेत्रफल के दो चतुर्भुज हैं। यदि ar(∆AQE) = 12 cm², तब ar(समान्तर चतुर्भुज FGBQ) =

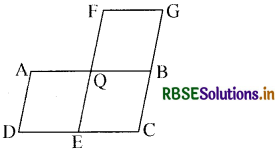
(A) 12 सेमी.²
(B) 20 सेमी.²
(C) 24 सेमी.²
(D) 36 सेमी.²
उत्तरः
(C) 24 सेमी.²

रिक्त स्थानों की पूर्ति करो

प्रश्न 1.
दो सर्वांगसम आकृतियों का क्षेत्रफल ............................. होता है।
उत्तरः
बराबर

प्रश्न 2.
एक ही आधार वाले और एक ही समान्तर रेखाओं के बीच स्थित समान्तर चतुर्भुज ................................ में बराबर होते हैं।
उत्तरः
क्षेत्रफल

प्रश्न 3.
समान्तर चतुर्भुज का क्षेत्रफल उसके ............................ और संगत शीर्षलम्ब का गुणनफल होता है।
उत्तरः
आधार

प्रश्न 4.
एक ही आधार वाले और बराबर क्षेत्रफलों वाले समान्तर चतुर्भुज एक ही ........................... के बीच स्थित होते हैं।
उत्तरः
समान्तर रेखाओं

प्रश्न 5.
किसी ∆ABC का क्षेत्रफल 24 वर्ग सेमी. है और ∆ABC की भुजाओं के मध्य बिन्दुओं को मिलाने पर ∆PQR बनता है। तब APQR का क्षेत्रफल ................................ है।
उत्तरः
6 वर्ग इकाई

प्रश्न 6.
समलम्ब चतुर्भुज का क्षेत्रफल उसकी ऊँचाई और समान्तर रेखाओं के योगफल के गुणनफल का ............................. होता है।
उत्तरः
आधा

प्रश्न 7.
समान्तर चतुर्भुज का विकर्ण इसको दो क्षेत्रफलों वाले ........................... में विभाजित करता है।
उत्तरः
बराबर, त्रिभुजों

प्रश्न 8.
किसी समान्तर चतुर्भुज PQRS के मध्य बिन्दु ABCD हैं। यदि क्षेत्रफल (PQRS) = 36 सेमी.² तब क्षेत्रफल (ABCD) = ..................................
उत्तरः
आधा

सत्य/असत्य-निम्नलिखित कथनों के लिए सत्य अथवा असत्य लिखिए

प्रश्न 1.
एक ही समान्तर रेखाओं के बीच स्थित समान्तर चतुर्भुज, आयत और त्रिभुजों के शीर्षलम्ब असमान होते हैं।
उत्तर:
असत्य

प्रश्न 2.
बराबर क्षेत्रफल वाले त्रिभुजों में, यदि एक त्रिभुज की एक भुजा दूसरे त्रिभुज की संगत भुजा के बराबर हो, तो उनके संगत शीर्षलम्ब भी बराबर होते हैं।
उत्तर:
सत्य

प्रश्न 3.
ABCD एक आयत है जिसमें O, कोई बिन्दु इसके अन्दर है। यदि क्षेत्रफल (∆AOD) = 3 सेमी.² और क्षेत्रफल (∆BOC) = 6 सेमी.², तब आयत ABCD का क्षेत्रफल 18 सेमी. है।
उत्तर:
सत्य

प्रश्न 4.
किसी त्रिभुज ABC की माध्यिकाएँ G पर मिलती हैं। यदि त्रिभुज ABC का क्षेत्रफल 27 सेमी.² हो तब त्रिभुज BGC का क्षेत्रफल \(\frac{27}{2}\) सेमी.² होगा।
उत्तर:
असत्य

प्रश्न 5.
एक आकृति का क्षेत्रफल उस आकृति द्वारा घेरे गये तल के भाग से सम्बद्ध एक संख्या होती है।
उत्तर:
सत्य

प्रश्न 6.
समान्तर चतुर्भुज का क्षेत्रफल उसके आधार और संगत शीर्षलम्ब का भागफल होता है।
उत्तर:
असत्य

प्रश्न 7.
किसी आयत की आसन्न भुजाओं के मध्य बिन्दुओं को मिलाने पर बनने वाली आकृति 24 सेमी.² क्षेत्रफल वाला समचतुर्भुज होगी जबकि आयत की भुजाएँ 8 सेमी. व 6 सेमी. की हैं।
उत्तर:
सत्य

अतिलघूत्तरात्मक प्रश्न:

प्रश्न 1.
किसी समान्तर चतुर्भुज का क्षेत्रफल 300 मी. है तथा ऊँचाई 15 मी. है तो उसका आधार क्या होगा?
हल:
समान्तर चतुर्भुज का आधार

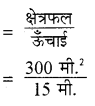
आधार = 20 मी.

प्रश्न 2.
एक त्रिभुजाकार भूखण्ड की ऊँचाई 105 मीटर तथा आधार 110 मीटर है तो क्षेत्रफल क्या होगा? हल-त्रिभुज का क्षेत्रफल
= \(\frac{1}{2}\) × आधार × ऊँचाई
= \(\frac{1}{2}\) × 110 × 105
= 5775 मी.²

प्रश्न 3.
किसी समलम्ब चतुर्भुज की ऊँचाई 10 सेमी. तथा समान्तर भुजाओं का योग 30 सेमी. हो तो समलम्ब चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
हल:
समलम्ब चतुर्भुज का क्षेत्रफल
= \(\frac{1}{2}\) × ऊँचाई × (समान्तर भुजाओं का योग)
= \(\frac{1}{2}\) × 10 × 30
= 10 × 15 = 150 सेमी.²

प्रश्न 4.
एक आयत और एक समान्तर चतुर्भुज एक ही आधार व एक ही समान्तर रेखाओं के मध्य स्थित हैं। यदि आयत की ऊँचाई 6 सेमी. तथा समान्तर चतुर्भुज का आधार 10 सेमी. है तो समान्तर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
हल:
∵ आयत व स.च. एक ही आधार व एक ही स. रेखाओं के बीच हैं।
∴ आयत की ऊँचाई = स.च. की ऊँचाई
स. च. का क्षेत्रफल = आधार × ऊँचाई
= 10 × 6 सेमी.²
= 60 सेमी.²

प्रश्न 5.
एक आयत का क्षेत्रफल 40 वर्ग सेमी. है और उसका आधार 5 सेमी. है। यदि उसी आधार व उन्हीं समान्तर रेखाओं के बीच एक त्रिभुज स्थित है तो त्रिभुज की ऊँचाई ज्ञात कीजिए।
हल:
एक ही आधार व एक ही समान्तर रेखाओं के मध्य किसी त्रिभुज का क्षेत्रफल आयत के क्षेत्रफल का आधा होता है। अतः
त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) सेमी.²
= 20 सेमी.²
पुनः त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) × आधार × ऊँचाई

प्रश्न 6.
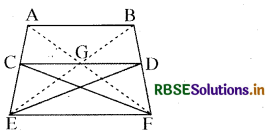
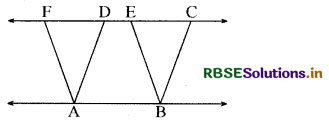
संलग्न चित्र में AB || CD || EE बताइये क्षेत्रफल के आधार पर कौन-कौन से त्रिभुज बराबर हैं और क्यों?

हल:
(i) ∆ABE व ∆ABF बराबर हैं, क्योंकि इनका आधार एक ही AB है व दोनों एक ही समान्तर रेखाओं AB व EF के मध्य बने हैं। अतः
∆ABE = ∆ABF
(ii) ∆CDE व ∆CDF बराबर हैं क्योंकि दोनों एक ही आधार CD व एक ही समान्तर रेखाओं CD व EF के बीच बने हैं। अत: ∆CDE = ∆CDF
(iii) ∆EFA व ∆EFB बराबर हैं क्योंकि दोनों एक ही आधार EF व समान्तर रेखाओं EF व AB के मध्य बने हैं। अत: ∆EFA = ∆EFB
(iv) ∆EFC, ∆EFD व. ∆EFG बराबर हैं, क्योंकि तीनों एक ही आधार EF व समान्तर रेखाओं EF व CD के बीच बने हैं। अत: ∆EFC = ∆EFD = ∆EFG

प्रश्न 7.
समलम्ब चतुर्भुज का क्षेत्रफल 80 सेमी. है। उसकी ऊँचाई 8 सेमी. है। चतुर्भुज की एक समान्तर भुजा 11 सेमी. है। दूसरी समान्तर भुजा की लम्बाई ज्ञात कीजिये।
हल:
समलम्ब चतुर्भुज का क्षेत्रफल
= \(\frac{1}{2}\) ऊँचाई × (पहली समान्तर भुजा + दूसरी समान्तर भुजा)
80 = \(\frac{1}{2}\) × 8 × (11 + दूसरी समान्तर भुजा)
दूसरी समान्तर भुजा = \(\left(\frac{80 \times 2}{8}\right)\) - 11
= 20 - 11
दूसरी समान्तर भुजा = 9 सेमी.

प्रश्न 8.
समान्तर चतुर्भुज का आधार 12 सेमी. और ऊँचाई 6.5 सेमी. है। इस स.च. के समान क्षेत्रफल वाले दूसरे समान्तर चतुर्भुज की ऊँचाई 10 सेमी. है, तो उसका आधार ज्ञात कीजिये। हल:
प्रथम स.च. का क्षेत्र. = आधार × ऊँचाई
= 12 × 6.5 सेमी.
= 78 सेमी. दोनों स.च. का क्षेत्रफल समान है। अतः
दूसरे स.च. का क्षेत्र. = आधार × ऊँचाई
78 सेमी.2 = आधार × 10 सेमी.
आधार = 78 सेमी.
आधार = 7.8 सेमी.

प्रश्न 9.
दो त्रिभुजों के आधार क्रमशः 8 सेमी. व 6 सेमी. हैं । यदि उनकी ऊँचाई क्रमशः 6 सेमी. व 8 सेमी. हो, तो उनके क्षेत्रफल का अनुपात ज्ञात कीजिये।
हल:
पहले त्रिभुज का क्षेत्रफल
= \(\frac{1}{2}\)आधार × ऊँचाई
= \(\frac{1}{2}\) × 8 × 6 सेमी.²
= 24 सेमी.²
दूसरे त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) × 6 × 8 सेमी.²
= 24 सेमी.²

अतः दोनों त्रिभुजों का अनुपात = 1 : 1 

लघूत्तरात्मक प्रश्न

प्रश्न 1.
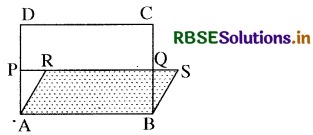
संलग्न चित्र में ABCD एक आयत है तथा ABSR एक स.च. है। यदि वQभुजा AD व BC के मध्य बिन्दु हों, तो छायांकित क्षेत्र का आयत ABCD से क्या सम्बन्ध है ? लिखिये।

हल:
आयत ABQP = \(\frac{1}{2}\) (आयत ABCD)
(∵ P व Q क्रमशः AD व BC के मध्य-बिन्दु
आयत ABQP व स.च. ABSR एक ही समान्तर रेखाओं व एक ही आधार के मध्य स्थित हैं। अतः
स.च. ABSR का क्षेत्रफल = आयत ABQP का क्षेत्रफल
स.च. ABSR का क्षेत्रफल = \(\frac{1}{2}\) (ABCD का क्षेत्रफल)
अतः छायांकित क्षेत्र ABSR, आयत ABCD का आधा है।

प्रश्न 2.
संलग्न चित्र में ABCD एक वर्ग है। FG || AB तथा क्षेत्र ABEF व क्षेत्र ABGH दो समान्तर चतुर्भुज हैं। ज्ञात कीजिये-

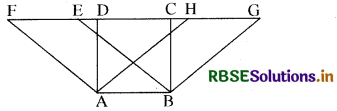
(i) स.च. ABEF व स.च. ABGH के क्षेत्रफलों में क्या सम्बन्ध है?
(ii) क्या दोनों स.च. क्षेत्रफल में वर्ग ABCD के बराबर हैं ? यदि हाँ, तो कारण भी लिखिये।
हल:
(i) स.च. ABEF व स.च. ABGH एक ही आधार व एक ही समान्तर रेखाओं के मध्य स्थित हैं। अत: ABEF का क्षेत्रफल ABGH के क्षेत्रफल के बराबर है।
(ii) हाँ, दोनों स.च. क्षेत्रफल में वर्ग ABCD के बराबर हैं। क्योंकि दोनों स.च. व वर्ग एक ही आधार AB व एक ही समान्तर रेखाओं FG व AB के मध्य स्थित हैं।

प्रश्न 3.
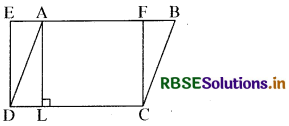
दी गई आकृति में, ABCD एक समान्तर चतुर्भुज है और EFCD एक आयत है। साथ ही AL ⊥ DC है। सिद्ध कीजिए कि
(i) ar (ABCD) = ar (EFCD)
(ii) ar (ABCD) = DC × AL

हल:
(i) चूँकि आयत एक समान्तर चतुर्भुज भी होता है, इसलिए
ar (ABCD) = ar (EFCD) (प्रमेय से)

(ii) उपर्युक्त परिणाम से,
ar (ABCD) = DC × FC .....(i)
∴ आयत का क्षेत्रफल = लम्बाई × चौड़ाई
∵ AL ⊥DC है, इसलिए AFCL एक आयत है।
अतः AL = FC ....... (ii)
∴ ar (ABCD) = DC × AL
[समीकरण (i) तथा (ii) से]

प्रश्न 4.
दर्शाइए कि त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है।
हल:
मान लीजिए ABC एक त्रिभुज है और AD उसकी एक माध्यिका है।

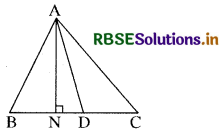
आप यह दर्शाना चाहते हैं कि
ar (ABD) = ar (ACD)
चूँकि त्रिभुज के क्षेत्रफल में शीर्षलम्ब सम्बद्ध होता है,
इसलिए आइए AN ⊥ BC खींचें।
अब, ar(ABD) = \(\frac{1}{2}\) × आधार × शीर्षलम्ब (∆ ABD का)
= \(\frac{1}{2}\) × BD × AN
= \(\frac{1}{2}\) × CD × AN (चूँकि BD = CD)
= \(\frac{1}{2}\) × आधार × शीर्षलम्ब (∆ ACD का)
= ar (ACD)

प्रश्न 5.
आकृति में, ABCD एक चतुर्भुज है और BE || AC इस प्रकार है कि BE बढ़ाई गई DC को E पर मिलती है। दर्शाइए कि त्रिभुज ADE का क्षेत्रफल चतुर्भुज ABCD के क्षेत्रफल के बराबर है।

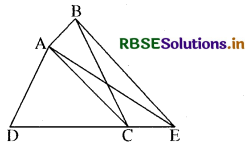
हल:
आकृति के अनुसार ∆ BAC और ∆ EAC एक ही आधार AC और एक ही समान्तर रेखाओं AC और BE के बीच स्थित हैं।
अतः, ar (BAC) = ar (EAC)
इसलिए, ar (BAC) + ar (ADC) = ar (EAC) + ar (ADC)
(एक ही क्षेत्रफल दोनों पक्षों में जोड़ने पर)
या ar (ABCD) = ar (ADE)

प्रश्न 6.
दो त्रिभुज एक ही आधार एवं एक ही समांतर रेखाओं के मध्य स्थित हैं। एक त्रिभुज की ऊँचाई 5 सेमी. तथा क्षेत्रफल 18 सेमी. है। दूसरे त्रिभुज की ऊँचाई बताइये।
हल:
दो त्रिभुज एक ही आधार व एक ही समांतर रेखाओं के मध्य स्थित हैं। अतः दोनों त्रिभुजों का क्षेत्रफल समान होगा।
एक त्रिभुज का क्षेत्रफल = 18 सेमी.²
एक त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) × आधार × ऊँचाई

प्रश्न 7.
एक त्रिभुज व एक स.च. का आधार 16 सेमी. है। दोनों एक ही समान्तर रेखाओं के मध्य स्थित हैं। त्रिभुज का क्षेत्रफल ज्ञात कीजिये। यदि स.च. की ऊँचाई 12 सेमी. है।
हल:
एक ही आधार व एक ही समान्तर रेखाओं के मध्य स्थित त्रिभुज का क्षेत्रफल स.च. के क्षेत्रफल का आधा होता है।
∴ त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) × स.च. का क्षेत्रफल
= \(\frac{1}{2}\) × आधार × ऊँचाई
त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) × 16 × 12 सेमी.²
= 8 × 12 सेमी.²
= 96 सेमी.²

प्रश्न 8.
संलग्न चित्र में DC || AB, DC = 2AB. ∆ADC व ∆ABC के क्षेत्रफल में सम्बन्ध बताइये।

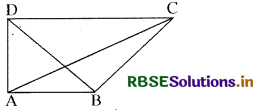
हल:
DC = 2AB
∆ADC का क्षेत्रफल = \(\frac{1}{2}\)AD × DC
= \(\frac{1}{2}\)AD × 2AB
= 2(\(\frac{1}{2}\) × AD × AB)
∆ADC का क्षेत्रफल = 2 × ∆ADB का क्षेत्रफल)
∵ ∆ABD व AABC एक समान्तर रेखाओं व एक ही आधार के मध्य हैं। अतः
∆ABD का क्षेत्रफल = ∆ABC का क्षेत्रफल
अत: ∆ADC का क्षेत्रफल = 2(∆ABC का क्षेत्रफल)
∴ ∆ADC का क्षेत्रफल ∆ABC के क्षेत्रफल का दुगुना होगा।

प्रश्न 9.
संलग्न चित्र में PQRS एक आयत है। XY || PQ, बिन्दु 0 रेखा XY पर स्थित कोई बिन्दु है। (∆OPQ + ∆ORS) का क्षेत्रफल एवं आयत PQRS के क्षेत्रफल में संबंध बताइये।

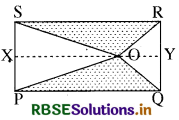
हल:
आयत XYPQ का क्षेत्रफल = 2 × (त्रिभुज OPQ का क्षेत्रफल)
आयत XYRS का क्षेत्रफल = 2 × (त्रिभुज ORS का क्षेत्रफल)
दोनों को जोड़ने पर-[आयत XYPQ का क्षे. + आयत XYRS का क्षेत्रफल]
= 2[∆OPQ का क्षेत्रफल + ∆ORS का क्षेत्रफल]
PQRS का क्षेत्रफल = 2(∆OPQ + ∆ORS) का क्षेत्रफल
या (∆OPQ + ∆ORS) का क्षेत्रफल
= \(\frac{1}{2}\) × (PQRS का क्षेत्रफल)
अत: (∆OPQ + ∆ORS) का क्षेत्रफल, आयत PQRS के क्षेत्रफल का आधा है।

प्रश्न 10.
श्रीमती ललिता के पास संलग्न चित्रानुसार एक कागज का टुकड़ा PQRS है। जिसमें SR || PQ, RQ ⊥ PQ. इसकी तीन भुजाएं SR = 9 सेमी., RQ = 8 सेमी. तथा PQ = 15 सेमी. हैं। उसने एक आकृति को इस टुकड़े के साथ जोड़कर एक बार आयत तथा दूसरी बार स.च. की आकृतियाँ प्राप्त की। दोनों ही बार प्राप्त आकृतियाँ क्षेत्रफल में बराबर थीं। आप बताइये कि उसने ऐसा किस प्रकार किया होगा? उस आकृति का नाम तथा नापें भी बताइये जिसे दोनों बार जोड़ा गया था।

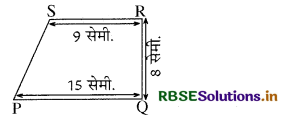
हल:
समकोण त्रिभुज की आकृति को पहली बार भुजा SP के सहारे तथा दूसरी बार भुजा RQ के सहारे रखा गया।

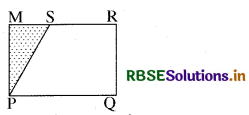
समकोण त्रिभुज की आकृति को भुजा SP के सहारे रखने पर आयत PMRQ प्राप्त होगा।
समकोण त्रिभुज की आकृति को भुजा RQ के सहारे रखने पर समान्तर चतुर्भुज PQMS प्राप्त होता है।

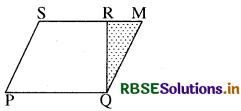
अतः उस आकृति का नाम समकोण त्रिभुज है तथा समकोण त्रिभुज की एक भुजा (लम्ब) = 8 सेमी. होगी। तथा दूसरी भुजा = (15 - 9) = 6 सेमी. होगी।

निबन्धात्मक प्रश्न

प्रश्न 1.
सिद्ध कीजिए कि एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित समान्तर चतुर्भुज क्षेत्रफल में बराबर होते हैं।
हल:
दिया है-दो समान्तर चतुर्भुज ABCD और ABEF एक ही आधार तथा एक ही समान्तर रेखाओं AB तथा FC के बीच स्थित हैं।

सिद्ध करना है-ar (समा. चतु. ABCD)
= ar (समा. चतु. ABEF)
उपपत्ति-चित्रानुसार AD || BC तथा FC एक तिर्यक रेखा उनको काटती है अतः ।
∠ADF = ∠BCE (संगत कोण) .....(i)
तथा AF || BE तथा FC एक तिर्यक रेखा उनको काटती है अतः
∠AFD = ∠BEC (संगत कोण).....(ii)
अब ∆ ADF तथा ∆ BCE में
AD = BC (समा. चतुर्भुज की सम्मुख भुजाएँ)
∠ADF = ∠ BCE .....[(i) से]
तथा ∠AFD = ∠ BEC .....[(ii) से]
अतः ∆ ADF = ∆ BCE
∴ ar (∆ ADF) = ar (∆ BCE) .....(iii)
समान्तर चतुर्भुज ABCD दो आकृतियों ABED तथा ∆ BCE से बना है। अतः
ar (समान्तर चतुर्भुज ABCD) = ar (चतु. ABED) + ar (∆ BCE)
= ar (चतु. ABED) + ar (∆ ADF) [(iii) से]
= ar (समा. चतु. ABEF)
∴ ar (समा. चतु. ABCD) = ar (समा. चतु. ABEF) (इति सिद्धम्)

प्रश्न 2.
सिद्ध करो कि यदि एक त्रिभुज तथा समान्तर चतुर्भुज एक ही आधार और समान्तर रेखाओं के बीच हैं, तो त्रिभुज का क्षेत्रफल, समान्तर चतुर्भुज के क्षेत्रफल का आधा होता है।
हल:
दिया है-एक समान्तर चतुर्भुज ABCE तथा एक त्रिभुज ABD एक ही आधार AB तथा एक ही समान्तर रेखाओं AB तथा DC के बीच स्थित हैं।

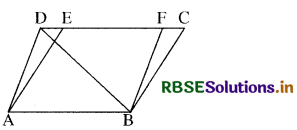
सिद्ध करना है-
ar (∆ ABD) = \(\frac{1}{2}\)ar (समा. चतु. ABCE)
रचना- AD के समान्तर एक रेखा BF खींची।
उपपत्ति- आकृति के अनुसार ABFD एक समान्तर चतुर्भुज है तथा BD इसका एक विकर्ण है। हम जानते हैं कि एक विकर्ण समान्तर चतुर्भुज को दो समान क्षेत्रफलों वाले त्रिभुजों में विभाजित करता है।
ar (∆ ABD) = ar (∆ BDF)
अत: ar (समा. चतु. ABFD) = 2 ar (∆ABD) ......(i)
तथा ar (समा. चतु. ABFD) = ar (समा. चतु. ........... ABCE).....(ii)
समीकरण (i) व (ii) से
2 ar (∆ ABD) = ar (समा. चतु. ABCE)
या ar (∆ ABD) = \(\frac{1}{2}\)ar (समा. चतु. ABCE) (इति सिद्धम्)

प्रश्न 3.
ABCD एक चतुर्भुज है। D से AC के समान्तर एक रेखा खींचो जो बढ़ाई हुई BC को P पर मिलती है। सिद्ध कीजिए कि ar (∆ ABP) = ar (चतुर्भुज ABCD).
हल:
चित्रानुसार ∆ ACP तथा ∆ ACD एक ही आधार AC तथा एक ही समान्तर रेखाओं AC तथा DP के बीच स्थित हैं।

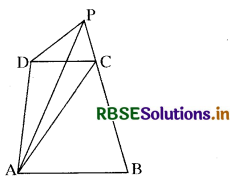
∴ ar (∆ ACP) = ar (∆ ACD)
दोनों पक्षों में ar (∆ ABC) जोड़ने पर
ar (∆ ABC) + ar (∆ ACP) = ar (∆ ABC) + ar (∆ ACD)
या ar (∆ ABP) = ar (चतुर्भुज ∆ BCD) (इति सिद्धम्)

प्रश्न 4.
चतुर्भुज ABCD के विकर्ण AC तथा BD परस्पर बिन्दु 0 पर इस प्रकार प्रतिच्छेदित करते हैं कि ar (∆ AOD) = ar (∆ BOC) है। सिद्ध कीजिए कि ABCD एक समलम्ब चतुर्भुज है।
हल:
प्रश्नानुसार ar (∆ AOD) = ar (∆ BOC)

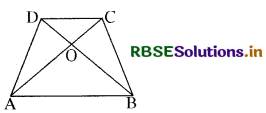
दोनों पक्षों में ar (∆ AOB) जोड़ने पर
ar (∆ AOD) + ar (∆ AOB) = ar (∆ BOC) + ar (∆ AOB)
या ar (∆ ABD) = ar (∆ ABC)
हम जानते हैं कि यदि दो त्रिभुज यदि क्षेत्रफल में समान हों तो वे एक ही आधार तथा एक ही समान्तर रेखाओं के बीच स्थित होते हैं। यहाँ ∆ ABD तथा ∆ ABC एक ही आधार AB पर तथा एक ही समान्तर रेखाओं AB तथा DC के बीच स्थित हैं और क्षेत्रफल में भी समान हैं।
या AB || DC
अब चतुर्भुज ABCD में AB || DC
अत: ABCD एक समलम्ब चतुर्भुज है क्योंकि समलम्ब चतुर्भुज में सम्मुख भुजाओं का एक युग्म समान्तर होता है।

प्रश्न 5.
एक ∆ ABC की माध्यिकाएँ बिन्दु G पर प्रतिच्छेदित करती हैं। सिद्ध कीजिए कि ar (∆ AGB) = \(\frac{1}{3}\)ar (∆ABC)
हल:
दिया है-एक ∆ ABC है जिसकी माध्यिकाएँ क्रमश: AD, BE तथा FC एक बिन्दु G पर प्रतिच्छेदित करती हैं।

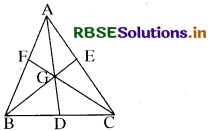
सिद्ध करना है
(∆ AGB) = \(\frac{1}{3}\) ar (∆ ABC)
उपपत्ति: ∆ ABC में AD एक माध्यिका है।
अतः
ar (∆ ABD) = ar (∆ ACD) .....(i)
क्योंकि माध्यिका त्रिभुज को समान क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है।
∆ GBC में GD एक माध्यिका है अतः
ar (∆ GBD) = ar (∆ GCD) .....(ii)
समीकरण (ii) में से (i) को घटाने पर
ar (∆ ABD) – ar (∆ GBD) = ar (∆∆CD) - ar (∆ GCD)
या ar (∆ AGB) = ar (∆ AGC) ........ (iii)
इसी प्रकार सिद्ध कर सकते हैं कि
ar (∆ AGB) = ar (∆ BGC) .....(iv)
समीकरण (iii) व (iv) से
ar (∆ AGB) = ar (∆ AGC) = ar (∆ BGC)
परन्तु ar (∆ ABC) = ar (∆ AGB) + ar (∆ ∆GC) + ar (∆ BGC) = 3 ar (∆∆GB)
[समीकरण (iii) व (iv) से]
∴ ar (∆ AGB) = \(\frac{1}{3}\) ar (∆ ABC)

प्रश्न 6.
सिद्ध कीजिए कि समान्तर चतुर्भुज का क्षेत्रफल इसके आधार और संगत शीर्ष लम्ब का गुणनफल होता है।
हल:
दिया है-एक समान्तर चतुर्भुज ABCD है जिसमें BC आधार और AL संगत शीर्षलम्ब हैं।

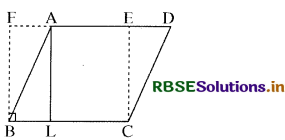
सिद्ध करना है-
ar (समान्तर चतुर्भुज ABCD) = BC × AL
रचना- AD भुजा पर CE तथा BF दो लम्ब खींचे तथा आयत BCEF को पूरा किया।
उपपत्ति- चित्रानुसार समान्तर चतुर्भुज ABCD तथा आयत BCEF एक ही आधार BC और एक ही समान्तर रेखाओं के बीच स्थित हैं। अतः
ar (समा. चतु. ABCD) = ar (आयत BCEF)
= BC × CE
= BC × AL [∵ CE = AL]
अतः ar (समा. चतु. ABCD) = BC × AL (इति सिद्धम्)

प्रश्न 7.
सिद्ध कीजिए कि किसी भी त्रिभुज का क्षेत्रफल इसकी भुजा तथा संगत शीर्षलम्ब के गुणनफल का आधा होता है।
हल:
दिया है-एक ∆ ABC है जिसमें आधार BC पर AL एक शीर्ष लम्ब है।

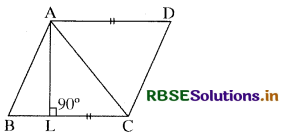
सिद्ध करना है:
ar (∆ ABC) = \(\frac{1}{2}\) × BC × AL
रचना: बिन्दु C तथा A से भुजा AB तथा BC के समान्तर रेखाएँ खींची जो परस्पर प्रतिच्छेद करती हैं।
उपपत्ति: समान्तर चतुर्भुज BCDA में AC विकर्ण है। अतः
ar (∆ ABC) = ar (∆ DAC) = \(\frac{1}{2}\)ar (समा. चतु. BCDA) ........ (i)
तथा ar(समा. चतु. BCDA) = BC × AL ....... (ii)
समीकरण (i) व (ii) से
ar (∆ ABC) = \(\frac{1}{2}\) BC × AL

प्रश्न 8.
सिद्ध करो कि समलम्ब चतुर्भुज का क्षेत्रफल इसकी ऊँचाई और समान्तर रेखाओं के योगफल के गुणनफल का आधा होता है।
हल:
दिया है-एक समलम्ब चतुर्भुज ABCD है जिसमें AB || DC, AB = a तथा DC = b है। भुजा AL = CM = h जहाँ DC भुजा पर AL तथा AB भुजा पर CM लम्ब हैं।

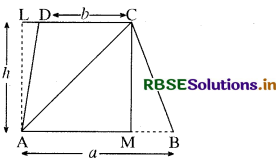
सिद्ध करना है:
ar (समलम्ब ABCD) = \(\frac{1}{2}\) × h × (a + b)
रचना: बिन्दु A को C से मिलाया।
उपपत्ति: ar (समलम्ब ABCD)
= ar × (∆ ADC) + ar (∆ ACB)
= \(\frac{1}{2}\) × DC × AL + \(\frac{1}{2}\) × AB × CM
= \(\frac{1}{2}\) × (DC + AB) × h [∵ AL = CM = h]
= \(\frac{1}{2}\) × (b + a) × h
= \(\frac{1}{2}\) × h × (a + b) (इति सिद्धम् )

प्रश्न 9.
दो त्रिभुज ABC और DBC एक ही आधार BC पर स्थित हैं तथा उनके शीर्ष A और D, रेखा BC के विपरीत ओर स्थित हैं, जिससे कि ar (∆ ABC) = ar (∆ DBC)। सिद्ध कीजिए कि BC, रेखाखण्ड AD को समद्विभाजित करता है।
हल:
प्रश्नानुसार ∆ABC और ∆DBC आपस में क्षेत्रफल में समान हैं तथा BC भुजा उभयनिष्ठ है।
∵ BC के संगत शीर्षलम्ब समान हैं अर्थात्

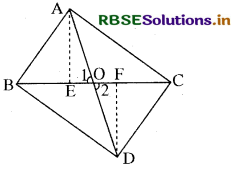
AE = DF ........ (i)
∆ AEO तथा ∆ DFO #
∠1 = ∠2 (शीर्षाभिमुख कोण)
∠AEO = ∠DFO (प्रत्येक 90°)
तथा AE = DF [(i) के अनुसार]
अतः सर्वांगसमता के नियम AAS के अनुसार
∆AEO ≅ ∆ DFO
अर्थात् AO = DO
क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं, अत: BC, भुजा AD को समद्विभाजित करती है।