RBSE Class 9 Maths Important Questions Chapter 8 Quadrilaterals

Rajasthan Board RBSE Class 9 Maths Important Questions Chapter 8 Quadrilaterals Important Questions and Answers.

RBSE Class 9 Maths Chapter 8 Important Questions Quadrilaterals

I. Multiple Choice Questions :
Choose the correct answer from the given options.

Question 1.
Which of the following is not true for a parallelogram?
(a)    Opposite sides are equal.
(b)    Opposite angles are equal.
(c)    Opposite angles are bisected by the diagonals.
(d)    Diagonals bisect each other.
Answer:
(c)    Opposite angles are bisected by the diagonals.

Question 2.
Three angles of a quadrilateral are 75°, 90° and 75°. The fourth angle is :
(a)    90°
(b) 95°
(c) 105°
(d) 120°
Answer:
(d) 120°

Question 3.
ABCD is a rhombus such that ∠ACB = 40°. Then ∠ADB is :
(a)    40°
(b) 45°
(c) 50°
(d) 60°
Answer:
(c) 50°

Question 4.
A diagonal of a rectangle is inclined to one side of the rectangle at 25°. The acute angle between the diagonal is :
(a)    55°
(b) 50°
(c) 40°
(d) 25°
Answer:
(b) 50°

Question 5.
The figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is square only if:
(a) ABCD is a rhombus.
(b) diagonals of ABCD are equal.
(c) diagonals of ABCD are perpendicular to each other.
(d) diagonals of ABCD are equal and perpendicular to each other.
Answer:
(d) diagonals of ABCD are equal and perpendicular to each other.

Question 6.
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle if:
(a) PQRS is a parallelogram.
(b) PQRS is a rectangle.
(c) the diagonals of PQRS are perpendicular to each other.
(d) the diagonals of PQRS are equal.
Answer:
(c) the diagonals of PQRS are perpendicular to each other.

Question 7.
If APB and CQD are two parallel lines, then the bisectors of ∠APQ, ∠BPQ, ∠CQP and ∠PQD form:
(a) a square
(b) a rhombus
(c) a rectangle
(d) any other parallelogram
Answer:
(c) a rectangle

Question 8.
D and E are mid-points of the sides AB and AC of ΔABC and O is any point on the side BC. O is joined to A. If P and Q are mid-points of OB and OC respectively, then ΔEQP is:
(a) a square
(b) a rectangle
(c) a rhombus
(d) a parallelogram
Answer:
(d) a parallelogram

Question 9.
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a rhombus if:
(a) ABCD is a parallelogram.
(b) ABCD is a rhombus.
(c) the diagonals of ABCD are equal.
(d) the diagonals of ABCD are perpendicular to each other.
Answer:
(c) the diagonals of ABCD are equal.

Question 10.
In the given figure, ABCD is a parallelogram and E is the mid-point of BC. Also, DE and AB when produced meet at F. Then

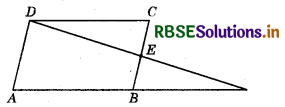
(a)    AF = \(\frac{3}{2}\)AB
(b)    AF = 2AB
(c)    AF = 3AB
(d)    AP² = 2AB²
Answer:
(b)    AF = 2AB

Question 11.
In the given figure, ABCD is a parallelogram in which ∠BDC = 45° and ∠BAD = 75°. Then, ∠CBD =?
(a) 45°
(b) 55°
(c) 60°
(d) 75°
Answer:
(c) 60°

Question 12.
In the given figure, ABCD is a parallelogram, M is the mid-point of BD and BD bisects ∠B as well as ∠D. Then, ∠AMB = ?

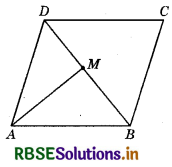
(a) 46°
(b)    60°
(c) 90°
(d) 30°
Answer:
(c) 90°

Question 13.
In the given figure, AD is a median of ΔABC and E is the mid-point of AD. If BE is joined and produced to meet AC in F, then AF = ?

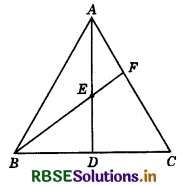
(a)    \(\frac{1}{2}\)AC
(b)    \(\frac{1}{3}\)AC
(c)    \(\frac{2}{3}\)AC
(d)    \(\frac{3}{4}\)AC
Answer:
(b)    \(\frac{1}{3}\)AC

Question 14.
The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O such that ∠DAC = 30° and ∠AOB = 70°. Then ∠DBC = ?

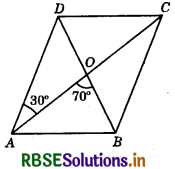
(a)    40°
(b)    35°
(c)    45°
(d)    50°
Answer:
(a)    40°

Question 15.
In the given figure, ABCD is a rhombus. Then:

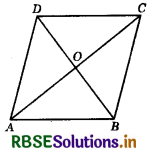
(a)    AC² + BD² = AB²
(b)    AC² + BD² = 2AB²
(c)    AC² + BD² = 4AB²
(d)    2(AC² + BD²) = 3AB²
Answer:
(c)    AC² + BD² = 4AB²
    
II. Fill in the Blanks :

Question 1.
If the angles of a quadrilateral are (4x)°, (7x)°, (15x)° and (10x)°. Then the smallest angle of this quadrilateral is _________.
Answer:
40

Question 2.
In figure, PQRS is a parallelogram in which a pair of opposite angles is given. The value of x is _________.

Answer:
15

Question 3.
ABCD is rhombus such that ∠ACB = 40°, then ∠ADB is _________.
Answer:
50

Question 4.
In the figure, ΔPQR is formed by joining the mid-points of sides BC, CA, and AB respectively. If AABC is an equilateral triangle with side 12 cm, then the length of PQ is    _________.

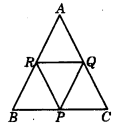
Answer:
6 cm

Question 5.
In a triangle, the line segment joining the mid-points of any given two sides is to the third side and is _________.
Answer:
Parallel, half of it.

III. True/False:
State whether the following statements are True or False.

Question 1.
A quadrilateral is a parallelogram if its opposite sides are parallel.
Answer:
True

Question 2.
In a parallelogram opposite angles are equal.
Answer:
True

Question 3.
Every square is a rectangle.
Answer:
True

Question 4.
In a parallelogram, diagonals bisect each other.
Answer:
True

Question 5.
Every square is a rhombus.
Answer:
True

Question 6.
The sum of the angles of a quadrilateral is 180°.
Answer:
True

Question 7.
In a parallelogram, the diagonals interesect at right angles.
Answer:
False

IV. Match the Columns :

Question 1.
Match the column I with the column II.

Column I	Column II
(1) Angle bisectors of a parallelogram form a	(i) parallelogram
(2) The quadrilateral formed by joining the mid-points of the pairs of adjacent sides of a square is a	(ii) rectangle
(3) The quadrilateral formed by joining the mid-points of the pairs of adjacent sides of a rectangle is a	(iii) square
(4) The figure formed by joining the mid-points of the pairs of adjacent sides of a quadrilateral is a	(iv) rhombus

Answer:

Column I	Column II
(1) Angle bisectors of a parallelogram form a	(ii) rectangle
(2) The quadrilateral formed by joining the mid-points of the pairs of adjacent sides of a square is a	(iii) square
(3) The quadrilateral formed by joining the mid-points of the pairs of adjacent sides of a rectangle is a	(iv) rhombus
(4) The figure formed by joining the mid-points of the pairs of adjacent sides of a quadrilateral is a	(i) parallelogram

V. Very Short Answer Type Questions :

Question 1.
Diagonals of a quadrilateral ABCD bisect each other. If ∠A = 35° then ∠B = 145°. Is it true? Also justify your answer.
Answer:
It is true that if ∠A = 35° then ∠B = 145°. It is given that ABCD is a quadrilateral and diagonals of quadrilateral ABCD bisect each other. Then, it should be a parallelogram.
Also, we know that ∠A and ∠B are adjacent angles of parallelogram ABCD ∠A + ∠B = 180°
⇒ 35° + 145° = 180°
Hence    ∠B = 145°.

Question 2.
In the following figure, ABCD and AEFG are two parallelograms. If ∠C = 60° then what is the value of ∠GFE?

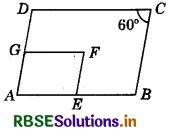
Answer:
∠A = ∠C    (Opposite angles of parallelogram ABCD are equal)
Also, AEFG is a parallelogram (Given)
⇒ ∠GFE = ∠A (Opposite angle of parallelogram are equal)
⇒ ∠GFE = 60°

VI. Short Answer Type Questions :

Question 1.
In quadrilateral ABCD, ∠A + ∠C = 140°, ∠A : ∠C = 1 : 3 and ∠B : ∠D = 5:6. Find the ∠A, ∠B, ∠C and ∠D.

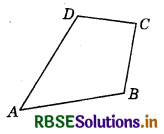
Answer:
In quadrilateral ABCD,
∠A + ∠C = 140°    .................... (1)
∠A : ∠C = 1 : 3 .................. (2)
and    ∠B : ∠D = 5 : 6    ................ (3)
Let ∠A = x and ∠C = 3x.
We know that, sum of angles of a quadrilateral = 360°
∠A + ∠B + ∠C + ∠D = 360°
⇒ ∠B + ∠D = 360° - (∠A + ∠C)
⇒ ∠B + ∠D = 360° - (35° + 105°) = 220°
Since,    ∠B : ∠D = 5 : 6
⇒ ∠B : ∠D = 5 : 6 
⇒ 5x + 6x = 11x
⇒ 11x = 220°
x = 20°
∠B = 5x = 5 × 20 = 100°
∠D = 6x = 6 × 20 = 120°
Hence, ∠A = 35°, ∠B = 100°, ∠C = 105° and ∠D = 120°.

Question 2.
In the adjoining figure, PQRS is a rhombus, SQ and PR are the diagonals of the rhombus intersecting at point O. If ∠OPQ = 35°, then find the value of ∠ORS + ∠OQP.

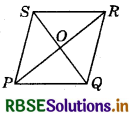
Answer:
Given : PQRS is a rhombus
⇒ PQRS is a parallelogram
Since,    PQ ∥ SR and PR is a transversal.
∴ ∠ORS = ∠OPQ = 35°    (Alternate interior angles)    ....................(1)
Also, diagonals of a rhombus bisect each other at right angle.
∴ ∠SOR = 90°    .............(2)
Now, in ΔSOR, ∠RSO + ∠SOR + ∠ORS = 180° (Angle sum property of triangles)
⇒ ∠RSO = 180° - ∠SOR - ∠ORS
⇒ ∠RSO = 180° - 90° - 35°
⇒ ∠RSO = 55° 
⇒ ∠OQP = 55°
(Alternate interior angles, since PQ ∥ SR and QS is a transversal) 

From equations (1) and (3), we get
∠ORS + ∠OQP = 35° + 55° = 90°

Question 3.
ABCD is a kite with AB = AD and CD = CR. Prove that the figure formed by joining the mid-points of the consecutive sides is a rectangle.
Answer:
We draw the figure as shown below.

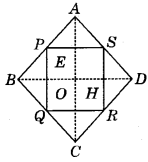
Let P, Q, R and S be the mid-points of the sides AB, BC, CD and DA respectively. Join AC and BD. Which intersects each other at O.
Now, in ΔABC, PQ ∥ AC and PQ = \(\frac{1}{2}\)AC ............ (1) (By mid-point theorem)
and in ΔACD, RS ∥ AC and RS = \(\frac{1}{2}\)AC .................(2) (By mid-point theorem)

From equations (1) and (2) we get,
PQ ∥ RS and PQ = RS (Since, a pair of opposite sides equal and parallel)
So, PQRS is a parallelogram
Also, AB = AD (Given)    ...................(1)
So, A lies on the perpendicular bisector of BD further
CB = CD (Given)    ......................(2)
So, C lies on the perpendicular bisector of BD.    .................(3)

From equations (2) and (3), AC is the perpendicular bisector of BD.
i.e.  AC ⊥ BD ⇒ ∠AOD = 90°
Now, clearly HS ∥ OE and SE ∥ OH
So, SEOH is a parallelogram.
Hence, ∠ESH = ∠EOH = 90°
So, parallelogram PQRS is a rectangle.

Question 4.
ABCD is a rhombus such that ∠ACB = 40°, then find ∠ADB.
Answer:
Given : ABCD is a rhombus.

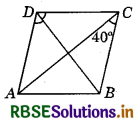
AB = CD = BC = AD
In ΔABC, AB = BC
∴ ∠ACB = ∠CAB = 40°
(Angles opposite to equal sides are equal)
Now, AB ∥ CD and AC is transversal.
∴ ∠DCA = ∠CAB = 40°    (Alternate angles)
Now,    ∠C = ∠BCD - ∠BCA + ∠DCA
= 40° + 40° = 80° 

We know that, ∠D + ∠C = 180° (Co-interior angles of a rhombus)
∠D =180° - 80° = 100°
∴ ∠ADB = \(\frac{1}{2}\)∠D = \(\frac{100^{\circ}}{2}\) = 50°

Question 5.
In the adjoining figure, P is the mid-point of side BC of a parallelogram ABCD, such that ∠BAP = ∠DAP. Prove that AD = 2 CD.

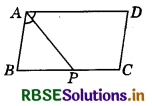
Answer:
Given : ABCD is a parallelogram. P is the mid-point of BC,
i.e. BC = 2BP ⇒ AD = 2BP
∠BAP = ∠DAP    .
AD = 2 CD
∠BAP = ∠DAP
∠DAP = ∠APB
∠BAP = ∠APB ⇒ BP = AB
(Sides opposite to equal angles of a triangle are equal)
AB = CD (Opposite sides of parallelogram)
BP = CD (∵ BP = AB) ...................(1)
BC = 2BP (Given)
⇒ AD = 2BP .................(2)
(∵ BC = AD, opposite sides of parallelogram)

From equations (1) and (2), we have :
AD = 2CD
Hence proved.

Question 6.
In quadrilateral ABCD, AP and BP are bisectors of ∠A and ∠B respectively, then find the value of x.
Answer:
From the fig.

∠1 = ∠2, ∠3 = ∠4    ...(1)
(AP and BP are bisectors of ∠A and ∠B.)

ABCD is quadrilateral,
So,    ∠A + ∠B + ∠C + ∠D = 360°    (Sum of all angles of a quad.)
∴ ∠1 + ∠2 + ∠3 + ∠4 + 130° + 60° = 360°
⇒ 2∠1 + 2∠3 + 190° = 360°    [From (1)]
⇒ 2∠1 + 2∠3 = 360° - 190° = 170°
⇒ ∠1 + ∠3 = \(\frac{170^{\circ}}{2}\) = 85°    ...(2)

In ΔAPB, ∠1 + x + ∠3 = 180°    (Angle sum property of a A)
⇒ ∠1 + ∠3 + x = 180°
⇒ 85° + x = 180°
∴ x = 180° - 85° = 95°
Hence,    x = 95°

Question 7.
The angle between two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 60°. Find the angles of the parallelogram.

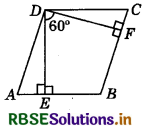
Answer:
Given : Parallelogram ABCD, in which ∠ADC and ∠ABC are obtuse angles. Now, DE and DF are two altitudes of parallelogram and angle between them is 60°.
Now, BEDF is a quadrilateral, in which
∠BED = ∠BFD = 90°
∴ ∠FBE = 360° - (∠FDE + ∠BED + ∠BFD)
(Angle sum property of a quadrilateral) = 360° - (60° + 90° + 90°) = 360° - 240° = 120°
Since, ABCD is a parallelogram.
∠ADC = 120°    [∵ ∠D = ∠B]
Now,    ∠A + ∠B = 180° (Co-interior angles of a parallelogram)
∴ ∠A = 180° - ∠B = 180° - 120° (∵ ∠FBE = ∠B)
⇒ ∠A = 60°
Also, ∠C = ∠A = 60°
(∵ Opposite angles of a parallelogram are equal.)
Hence, angles of the parallelogram are 60°, 120°, 60° and 120°, respectively.

Question 8.
PQ and RS are two equal and parallel line segments. Any point M not lying on PQ or RS is joined to Q and S and lines through P parallel to QM and through R parallel to SM meet at N. Prove that line segments MN and PQ are equal and parallel to each other.
Answer:
It is given that PQ = RS and PQ ∥ RS.

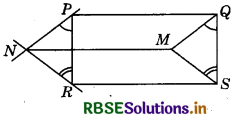
Since, a pair of opposite side of a quadrilateral PQSR is equal and parallel.
Therefore, PQSR is a parallelogram.
So,    PR = QS and PR ∥ QS
Now,    PR ∥ QS
Therefore,    ∠RPQ + ∠PQS = 180°
(Interior angles on the same side of the transversal)

i.e.    ∠RPQ + ∠PQM + ∠MQS = 180°
Also,    PN ∥ QM (By Construction)
Therefore, ∠NPQ + ∠PQM = 180° 
i.e. ∠NPR + ∠RPQ + ∠PQM = 180° ...........(3)
So, ∠NPR = ∠MQS [From equation (2) and (3)] ...........(4)
Similarly ∠NRP = ∠MSQ, ..........(5)

In ΔPNR and ΔQMR PR = QS [Using equation (1)]
∠NPR = ∠MQS [Using equation (4)]
∠NRP = ∠MSQ [Using equation (5)]
∠PNR = ΔQMS
So, PN = QM and NR = MS
PN = QM and PN ∥ QM, we have PQMN is a parallelogram.
(Since, a pair of opposite side of a quadrilateral equal and parallel)
So,    NM = PQ and NM ∥ PQ.
Hence proved.

Question 9.
In the given figure, ABCD is a square and EF ∥ BD. M is the mid-point of EF. Prove that AM bisects ∠BAD.

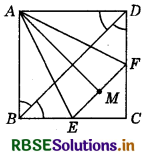
Answer:
Given : ABCD is a square and BD is a diagonal.
∠CBD = ∠CDB = x 90° = 45°
(∵ Diagonal of a square bisect each angle at the vertex)
Also, EF ∥ BD    (Given)
So, ∠CEF = ∠CBD = 45°    (Corresponding angles)
and ∠CFE = ∠CDB = 45°    .    (Corresponding angles)
⇒ CE = CF (∵ Sides opposite to equal angles are equal.)
⇒ BC - CE = CD - CF    (∵ BC = CD)
⇒ BE = DF     ................(1)
Now, in AABE and AADF,    
AB = AD (Adjacent sides of a square)
∠ABE = ∠ADF (Each 90°)
BE = DF [From equation (1)]

So, ΔABE ≅ ΔADF (By SAS congruence rule)
Then, AE = AF (By CPCT)    .........(2)
and ∠BAE = ∠DAF .............(3)
Now, in ΔAEM and ΔAFM,    
AE = AF [From equation (2)]
ME = MF (M is mid-point of EF)
AM = AM (Common side)
ΔAEM ≅ ΔAFM (By SSS congruence rule)
So, ∠EAM = ∠FAM    (By CPCT)    ...........(4)

On adding equations (3) and (4), we get
∠BAE + ∠EAM = ∠DAF + ∠FAM
⇒ ∠BAM = ∠DAM
i.e. AM bisects ∠BAD.
Hence proved.

Question 10.
ABCD is a parallelogram in which P and Q are mid-points of opposite sides AB and DC (given in figure). If AQ intersects DP at S and BQ intersects CP at R, show that:

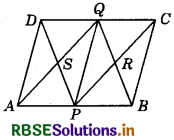
(i) APCQ is a parallelogram.
(ii) DPBQ is a parallelogram.
(iii) PSQR is a parallelogram.
Answer:
Given : ABCD is a parallelogram.
∴    AB ∥ DC, AB = DC
and AD ∥ BC, AD = BC
P and Q are mid-points of sides AB and CD.
(i) In quadrilateral APCQ,
AP ∥ QC [∵ AB ∥ DC]    ...................(1) 

Now,    AP = \(\frac{1}{2}\)AB, QC = \(\frac{1}{2}\)DC ..................    (2)
(∵ P and Q are mid-points of AB and CD, respectively.)
Since,    AB = DC    (Given)
⇒ \(\frac{1}{2}\)AB = \(\frac{1}{2}\)CD
⇒ AP = QC    [Using equation (2)]
Thus, we have AP ∥ QC and AP = QC
Hence, APCQ is a parallelogram.

(ii) Similarly, in quadrilateral DPBQ,
BP ∥ QD and BP = QD
DPBQ is a parallelogram.

(iii) Since, DPBQ is a parallelogram,
∴ DP ∥ QB
⇒ SP ∥ QR .................(3)
and APCQ is also a parallelogram.
∴ AQ ∥ PC
SQ ∥ PR ..............(4)
From equations (3) and (4), we have :
SP ∥ QR and SQ ∥ PR
Hence, PSQR is also a parallelogram.
Hence proved.

Question 11.
In the following figure, ABCD is a rhombus. If ∠ABC = 68°, then determine ∠ACD.

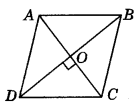
Answer:
Given : ABCD is a rhombus.
⇒ ABCD is a parallelogram
⇒ ∠ADC = ∠ABC = 68° (v Opposite angles of a parallelogram are equal.)
∠ODC = \(\frac{1}{2}\)∠ADC ( Diagonal DB of rhombus ABCD bisects its ∠ABC and ∠ADC)
∠ODO = \(\frac{1}{2}\) × 68°= 34°

Now, in ∠OCD
∠OCD + ∠ODC + ∠COD = 180° (Angle sum property of a triangle)
∠OCD + 340 + 90° = 180° (∵ ∠COD = 90°, diagonals of a rhombus bisect each other at right angles)
⇒ ∠OCD + 124° = 180°
⇒ ∠OCD = 180° - 124°
⇒ ∠OCD = 56° or ∠ACD = 56°

Question 12.
In the given figure, ABCD is a square, if ∠PQR = 90° and PB - QC = DR, then prove that QB = RC, PQ = QR and ∠QPR = 45°.

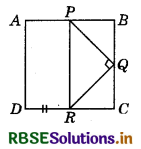
Answer:
Given : ABCD is a square, ∠PQR = 90° and PB = QC = DR.
To prove : QB = RC, PQ = QR and ∠QPR = 450
Proof: Since, ABCD is a square.
BC = CD
But QC = DR (Given)
⇒ BC - QC = CD - DR
⇒ QB = RC ................. (1)

Now, in ΔPBQ and ΔQCR, PB = QC (Given)
BQ = CR [From equation (1)]
∠PBQ = ∠QCR = 90°
∴ ΔPBQ ≅ ΔQCR (By SAS congruence rule)
So, PQ = QR (By CPCT)
Also, ∠BPQ = ∠CQR and ∠BQP = ∠CRQ

Now, since APQR is an isosceles right angled triangle.
So, ∠PRQ + ∠QPR + ∠PQR = 180° (Angle sum property of triangle)
⇒ ∠QPR + ∠QPR + 90° = 180° (Since, ∠PQR is isosceles)
⇒ ∠QPR = 90°
∴ ∠QPR = 45°
Hence proved.
  
VII. Long Answer Type Questions:

Question 1.
Prove that the opposite angles of an isosceles trapezium are supplementary.
Answer:
Let ABCD be an isosceles trapezium AB ∥ DC and AD = BC.

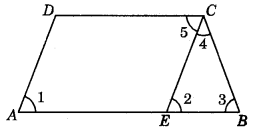
Through C, draw CE ∥ DA, AB ∥ DC  i.e., AE ∥ DC and CE ∥ DA    (By construction)
AECD is a parallelogram AD = EC (Opp. sides of a ∥gm)
AD = BC    (Given)
BC = EC
In ΔCEB, BC = EC
∠3 = ∠2 (Angles opp. equal sides are equal.) ...(1)

As DA ∥ CE and AE is a transversal.
∠1 = ∠2 (Corresponding ∠s) ...(2)
Also AE ∥ DC and CE is a transversal
∠5  = ∠2 (Alternate ∠s)
Now ∠A + ∠C  = ∠1 + (∠5 + ∠4)
⇒ ∠A + ∠C = ∠2 + ∠2 + ∠4 [Using (2) and (3)]
∠A + ∠C = ∠2 + ∠3 + ∠4 [Using (1)]
∠A + ∠C = 180° (Sum of ∠s of a Δ = 180°)
Now    ∠A + ∠B + ∠C + ∠D = 360°    
∠B + ∠D + 180    = 360° (Sum of ∠s of quadrilateral)
⇒ ∠B + ∠D = 180° (∵ ∠A + ∠C= 180°)
Hence, the opposite angles of an isosceles trapezium are supplementary.
Hence proved. 

Question 2.
P, Q,R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD, such that AC ⊥ BD. Prove that PQRS is a rectangle.
Answer:
In the figure:

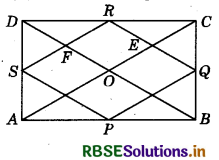
AC ⊥ BD
∠COD = ∠AOD = ∠AOB = ∠COB = 90°
In ΔADC, by mid-point theorem
SR ∥ AC and SR = \(\frac{1}{2}\)AC
Similarly in ΔABC, PQ ∥ AC and PQ = \(\frac{1}{2}\)AC
From equations (1) and (2) PQ ∥ SR and PQ = SR = \(\frac{1}{2}\)AC
Similarly, SP ∥ RQ and SP = RQ = \(\frac{1}{2}\)BD
In quadrilateral EDFR, DE ∥ FR, OF ∥ ER
∠EOF = ∠ERF = 90°
Hence, PQRS is a rectangle.

Question 3.
E is mid-point of the median AD of AABC and BE is produced to meet AC at F. Show that AF = \(\frac{1}{2}\)AC.

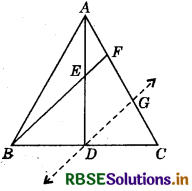
Answer:
Through D, draw a line parallel to BF to meet AC at G.
In ΔADG, E is mid-point of side AD and DG ∥ BF i.e.
DG ∥ EF, therefore by converse of mid-point theorem,
F is mid-point of AG i. e. AF = FG.    ..........(i)
In ABCF, D is mid-point of side BC and DG ∥ BF, therefore, by converse of mid-point theorem, G is mid-point of CF,
i.e. FG = GC .......(ii)
From (i) and (ii), we get:
AF = FG = GC ........(iii)
Now    AC = AF + FG + GC = AF + AF + AF [Using (iii)]
⇒ AC = 3AF ⇒ AF = \(\frac{1}{3}\)AC
Hence Proved.