RBSE Class 9 Maths Important Questions Chapter 7 Triangles

Rajasthan Board RBSE Class 9 Maths Important Questions Chapter 7 Triangles Important Questions and Answers.

RBSE Class 9 Maths Chapter 7 Important Questions Triangles

I. Multiple Choice Questions:
Choose the correct answer from the given four options.

Question 1.
In triangles ABC and DEF, AB = FD and ∠A = ∠D. The two triangle will be congruent by SAS axiom if:
(a) BC = EF
(b) AC = DE
(c) AC = EF
(d) BC = DE
Answer:
(b) AC = DE

Question 2.
Which of the following is not a interior for congruency of triangles? '
(a) SAS
(b) ASA
(c) SSA
(d) SSS
Answer:
(c) SSA

Question 3.
If it is given that ∆ABC ≅ ∆FDE, AB = 5 cm, ∠B = 40° and ∠A = 80°. Then which of the following is true?
(a) DF = 5 cm, ∠F = 60°
(b) DF = 5 cm, ∠E = 60°
(c) DF = 5 cm, ∠E = 60°
(d) DE = 5 cm, ∠D = 40°
Answer:
(b) DF = 5 cm, ∠E = 60°

Question 4.
In the adjoining figure, ABCD is a quadrilateral in which AD = CB and AB = CD, then ∠ACB is equal to:

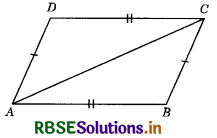
(a) ∠ACD
(b) ∠BAC
(c) ∠CAD
(d) ∠BAD
Answer:
(c) ∠CAD

Question 5.
In the adjoining figure, AC = BD. If ∠CAB = ∠DBA, then ∠ACB is equal to:

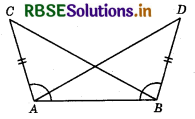
(a) ∠BAD
(b) ∠ABC
(c) ∠ABD
(d) ∠BDA
Answer:
(d) ∠BDA

Question 6.
In the adjoining figure, AB = AC and BD = CD. The ratio ∠ABD : ∠ACD A is:

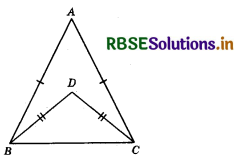
(a) 1:1
(b) 2 : 1
(c) 1 : 2
(d) 2 : 3
Answer:
(a) 1:1

Question 7.
In AQPR, if ∠R > ∠Q, then :
(a) QR > PR
(b) PQ > PR
(c) PQ < PR
(d )PR < PQ Answer: (b) PQ > PR

Question 8.
Two sides of a triangles are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be :
(a) 3.6 cm
(b) 4.1 cm
(c) 3.8 cm
(d) 3.4 cm
Answer:
(d) 3.4 cm

Question 9.
In the adjoining figure, PQ > PR. If OQ and OR are bisectors of ∠Q and ∠R respectively, then:

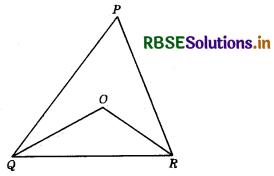
(a) OQ = OR
(b) OQ < OR
(c) OQ ≤ OR
(d) OQ > OR
Answer:
(d) OQ > OR

Question 10.
If triangle ABC is obtuse angled and ∠C is obtuse, then
(a) AB > BC
(b) AB = BC
(c) AB < BC (d) AC > AB
Answer:
(a) AB > BC

Question 11.
In the adjoining figure, ABCD is a quadrilateral in which BN and DM are drawn perpendiculars to AC such that BN = DM. If OB = 4 cm, then BD is:

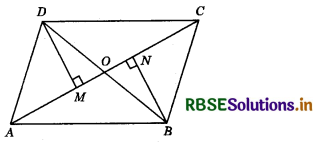
(a) 6 cm
(b) 8 cm
(c) 10 cm
(d) 12 cm
Answer:
(b) 8 cm

Question 12.
D is a point on the side BC of AABC such that AD bisects ∠BAC, then :
(a) BD = CD
(b) BA > BD
(c) BD > BA
(d) CD > CA
Answer:
(b) BA > BD

Question 13.
If AB = QR, BC = PR and CA = PQ, then :
(a) ∆ABC ≅ ∆PQR
(b) ∆CBA ≅ ∆PQR
(c) ∆BAC ≅ ∆RPQ
(d) ∆PQR ≅ ∆BCA
Answer:
(b) ∆CBA ≅ ∆PQR

Question 14.
Which is true?
(a) A triangle can have two right angles.
(b) A triangle can have two obtuse angles.
(c) A triangle can have two acute angles.
(d) An interior angle of a triangle is less them either of the interior opposite angles.
Answer:
(c) A triangle can have two acute angles.

Question 15.
In the given figure, BE ⊥ CA and CF ⊥ BA such that BE = CF.
Then which of the following is true?

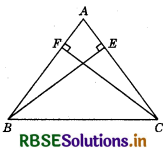
(a) ∆ABE ≅ ∆ACF
(b) ∆ABE ≅ ∆AFC
(c) ∆ABE ≅ ∆CAF
(d) ∆ABE ≅ ∆FAC
Answer:
(a) ∆ABE ≅ ∆ACF

Question 16.
In the given figure, AE = DB, CB = EF and ∠ABC = ∠FED. Then, which of the following is true?

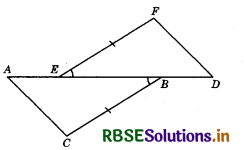
(a) ∆ABC ≅ ∆DEF
(b) ∆ABC ≅ ∆EFD
(c) ∆ABC ≅ ∆FED
(d) ∆ABC ≅ ∆DEF
Answer:
(a) ∆ABC ≅ ∆DEF

II. Fill in the Blanks:

Question 1.
In the figure, if AB = AC, then value of x is _________ .

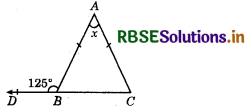
Answer:
70°

Question 2.
If AB = QR, BC = PR and CA = PQ, then ∆ABC ≅ __________ .

Answer:
∆QRP

Question 3.
In the figure, if OA = OB, OD = OC, then ∆AOD ≅ ∆BOC by congruence rule ___________ .

Answer:
SAS

Question 4.
In the figure, the ratio ∆ABD : ∆ACD is ___________ .

Answer:
1 : 1

Question 5.
In ∆PQR, ∠P = 60° and ∠Q = 50°, then the longest side of the triangle is ___________ .
Answer:
PQ

III. True/False:
State whether the following statements are True or False.

Question 1.
Two figures are congruent if they are of the same shape and of the same size.
Answer:
True

Question 2.
If two triangles ∆ABC and ∆PQR are congruent, then it is expressed as ∆ABC ≅ ∆PQR.
Answer:
True

Question 3.
If two sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle, then the two triangles are congruent.
Answer:
True

Question 4.
If two angles and one side of one triangle are equal to two angles and corresponding side of the other triangle, then the two triangles are congruent.
Answer:
True

Question 5.
In a triangle sum of two sides is smaller than the third side.
Answer:
False

Question 6.
In a triangle sum of two angles is greater than the third angle.
Answer:
False

Question 7.
In a triangle sum of two sides is greater than the third side.
Answer:
True

IV. Match the Columns:

Match the column I with the column II.

Column I	Column II
(1) In ∆ABC, if AB - AC and ∠A - 70°, then ∠C = .................	(i) less
(2) The vertical angle of an isosceles triangle is 120°. Each base angle is ……………..	(ii) greater
(3) The sum of three medians of a triangle is .................. than the perimeter.	(iii) 30°
(4) In a triangle, the sum of any two sides is always ……………. than the third side.	(iv) 55°

Answer:

Column I	Column I
(1) In ∆ABC, if AB - AC and ∠A - 70°, then ∠C = .................	(iv) 55°
(2) The vertical angle of an isosceles triangle is 120°. Each base angle is ……………..	(iii) 30°
(3) The sum of three medians of a triangle is .................. than the perimeter.	(i) less
(4) In a triangle, the sum of any two sides is always ……………. than the third side.	(ii) greater

V. Very Short Answer Type Questions:

Question 1.
In a triangle ABC, BC = AB and ∠B = 80°, then find the value of ∠A.
Answer:

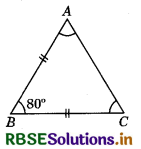
∆ABC is an isoscales triangle (∵ AB = BC)
⇒ ∠A = ∠C
In ∆ABC, ∠A + ∠B + ∠C = 180° (Angle sum property of a triangle)
⇒ ∠A + 80° + ∠A = 180°
⇒ 2∠A = 180 - 80° = 100°
⇒ ∠A = \(\frac{100}{2}\) = 50°
∠A = ∠C = 50°

Question 2.
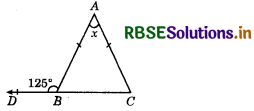
In the figure, if AB = AC, then find x.

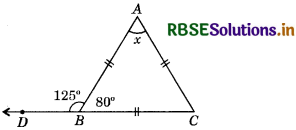
Answer:
In ∆ABC,
∠ABD + ∠ABC = 180° (Linear pair angles)
⇒ 125° + ∠ABC = 180°
⇒ ∠ABC = 180 - 125 = 55°
⇒ ∠ACB = 55°.
(∵ AB = AC given and ∴ ∠ABC = ∠ACB)
Now in ∆ABC,
∠A + ∠B + ∠C = 180°
⇒ x + 55° + 55° = 180°
⇒ x + 110 = 180
⇒ x = 180 - 110 = 70°

Question 3.
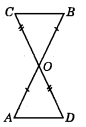
In the given figure, if OA = OB, OD = OC then ∆AOD ≅ ∆BOC by which congruency rule?

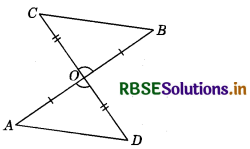
Answer:
In ∆AOD and ∆BOC

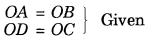
and ∠AOD = ∠BOC (Vertically opposite angles)
⇒ By SAS, ∆AOD ≅ ∆BOC.

Question 4.
In two triangles ABC and DEF, ∠A = ∠D, ∠B = ∠E and AB = EF, then are the two triangles congruent? If yes, by which congruency rule?
Answer:

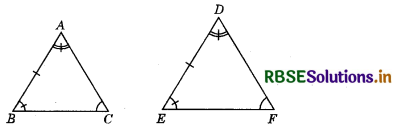
Yes, the two triangles are congruent by ASA congruency rule as ∠A = ∠D, ∠B = ∠E and AB = DF.

Question 5.
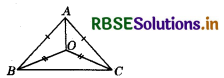
In the given figure, AD is the median, then find ∠BAD.

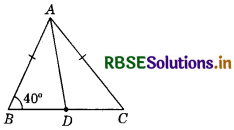
Answer:
From the given figure :
∠B = ∠C = 40° (∵ AB = AC given)
Now, ∠A + ∠B + ∠C = 180
⇒ ∠A = 180 - (40 + 40) = 180 - 80 = 100°
Also ΔABD ≅ ΔACD
BD = DC
and AD = AD
∴ By SSS, ΔABD ≅ ΔACD
⇒ ∠BAD = ∠CAD
⇒ ∠BAD = ∠CAD = \(\frac{\angle \mathrm{BAC}}{2}\) = \frac{100}{2} = 50°

VI. Short Answer Type Questions:

Question 1.
In the given figure, ΔABC is an equilateral triangle. If altitude AD is drawn from the vertex A, then prove that AB = AC = 2BD.

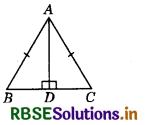
Answer:
Given: In ΔABC, AB = AC = BC (Equilateral
triangle) and AD ⊥BC (Altitude on base)
To prove: AB = AC = 2BD
Proof: In ΔADB and ΔADC,
AB = AC (Given)
AD = AD (Common side)
and ∠ADB = ∠ADC (Each 90°)
∴ ΔADB = ΔADC
Then, BD = DC
⇒ BC = 2BD
∵AB = AC = BC
∴ AB = AC = 2BD
Hence Proved.

Question 2.
In the given figure, PQ > PR, QS and RS are the bisectors of ∠Q and ∠R respectively, then find the relation between the sides SQ and SR.
Answer:
Given: PQ >PR
⇒ ∠PRQ > ∠PQR
(Since, angle opposite to longer side is greater.)
⇒ \(\frac{1}{2}\)∠PRQ > \(\frac{1}{2}\)∠PQR
⇒ ∠SRQ > ∠SQR (Since, QS and RS are the bisectors of ∠Q and ∠R, respectively.)
∴ SQ > SR
(Since, side opposite to greater angle of a triangle is longer.)

Question 3.
In ∆ABC, if ∠A = 40° and ∠B = 60°, then find the longest side of ∆ABC.
Answer:

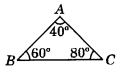
In ∆ABC, ∠A + ∠B + ∠C = 180°
(By angle sum property of a triangle)
⇒ ∠C = 180° - 100° = 80°
As, 80° > 60° ⇒ ∠C > ∠B
⇒ AB > AC
(∵ Side opposite to greatest angle is longest.)

Question 4.
Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer.
Answer:
No, it is not possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm, because here we see that sum of the lengths of two sides is equal to third side, i.e. 4 + 3 = 7.
We know that, the sum of any two sides of a triangle is greater than its third side, so, construction of given sides of triangle is not possible.

Question 5.
Prove that the perimeter of a triangle is greater than the sum of its three medians.
Answer:

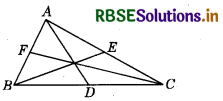
Consider ABC is a triangle and AD, BE and CF are the medians of ∆ABC. We know that, the sum of any two sides of a triangle is greater than twice the median drawn to the third side.
∴ AB + AC > 2AD ......... (1)
AB + BC > 2BE ......... (2)
and BC + AC > 2CF .......... (3)
On adding equations (1), (2) and (3), we get:
2(AB + BC + AC) > 2(AD + BE + CF)
∴ AB + BC + AC > AD + BE + CF
Hence, the perimeter of a triangle is greater than the sum of its three medians.
Hence proved.

Question 6.
In the given figure, if l || m, ∠ABC = ∠ABD = 40° and ∠BAC = ∠BAD = 90°, then prove that ∆BCD is an isosceles triangle.

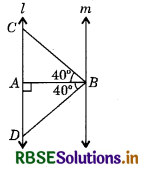
Answer:
In ∆BAC, ∠ACB + ∠ABC + ∠BAC = 180°
(By angle sum property of a triangle)
∴ ∠ACB + 40° + 90° = 180°
(∵ ∠ABC = 40° and ∠BAC = 90°)
⇒ ∠ACB = 180° - (40° + 90°)
= 180° - 130° = 50° and in ∆BAD, ∠BAD + ∠ADB + ∠ABD = 180°
(By angle sum property of a triangle)
⇒ 90° + ∠ADB + 40° = 180° (∵ ∠BAD = 90° and ∠ABD = 40°)
⇒ ∠ADB = 180° - 130° = 50°
In ∆BCD, ∠BCD = ∠CDB = 50°
(∵ ∠BCD = ∠ABC = 50° and ∠BDA = ∠ADB = 50°)
We know that, if two angles of a triangle are equal, then it is •an isosceles triangle.
So, ∆BCD is an isosceles triangle.
Hence proved.

Question 7.
In the given figure, AD bisects ∠A. Then, find the relation between the sides AB, AC and DC.

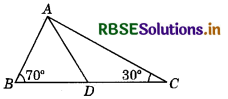
Answer:
Given, AD is the bisector of ∠BAC.
In ∆ABC, sum of three angles of a triangle is 180°.
∴ ∠A = 180° - (∠B + ∠C)
= 180° - (70° + 30°) = 80°
⇒ ∠BAD = ∠DAC
= \(\frac{80^{\circ}}{2}\) = 40° (Since, AD is the bisector of ∠A.)
In ∆ABD, ∠ADB = 180° - (∠BAD + ∠ABD)
(Since, sum of three angles of a triangle is 180°.)
= 180° - (40° + 70°) = 70°
and ∠DBA = ∠ADB
⇒ AD =AB
(Since, sides opposite to equal angles of a triangle are equal.)
In ∆ADC, ∠ADC = 180° - (∠DAC + ∠ACD)
(Since, sum of three angles of a triangle is 180°.)
= 180° - (40° + 30°) = 110°
and ∠DCA < ∠CAD < ∠ADC
(∵ ∠DCA = 30°, ∠CAD = 40° and ∠ADC =110°)
⇒ AD < DC < AC
But AB = AD
Therefore, AB < DC < AC

Question 8.
In ∆ABC, the sides AB, AC are equal and the base BC is produced to any point D. From D, DE is drawn perpendicular to BA produced and DF perpendicular to AC produced. Prove that BD bisects ∠EDF.
Answer:
Given: In ∆ABC, AB = AC and the base BC is produced to D. From D, DE is drawn perpendicular to BA produced to E and DF is perpendicular to AC produced to F.
To prove: BD bisects ∠EDF, i.e. ∠3 = ∠4
Proof: In ∆ABC, AC = AB (Given)
⇒ ∠1 = ∠2 ......... (1)
(Since, angles opposite to equal sides of a triangle are equal.)
In right-angled ∆BED, we have :
∠1 + ∠3 + ∠BED = 180° (By angle sum property of a triangle)
⇒ ∠l + ∠3 + 90° = 180° (∵ DE ⊥ BE ⇒ ∠BED = 90°)
⇒ ∠1 + ∠3 = 90°
⇒ ∠3 = 90° - ∠1 ........ (2)
In right-angled ∆CFD, we have:
∠4 + ∠5 + ∠CFD = 180° (By angle sum property of a triangle)
⇒ ∠4 + ∠5 + 90° = 180° (∵ DE ⊥ BE ⇒ ∠CFD = 90°)
⇒ ∠4 + ∠5 = 90°
⇒ ∠4 = 90° - ∠5
⇒ ∠4 = 90° - ∠2 ......... (3)
From equations (1), (2) and (3),
∠3 = ∠4
Hence, BD bisects ∠EDF.

VII. Long Answer Type Questions

Question 1.
In the given figure, QX and RX are bisectors of ∠PQR and ∠PRQ respectively of ∆PQR. If XS ⊥ QR and XT ⊥ PQ, then prove that ∆XTQ ≅ ∆XSQ and PX bisects ∠P.

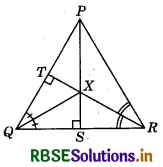
Answer:
Given : QX and RX are the bisectors of ∠PQR and ∠PRQ, respectively. Also, XS ⊥ QR and XT ⊥ PQ.
To prove: ∆XTQ ≅ ∆XSQ and PX bisects ∠P.

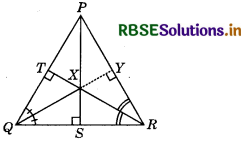
Construction : Draw XY ⊥ PR.
Proof : In ∆XTQ and ∆XSQ, we have:
∠TQX = ∠SQX
(Since, QX is the bisector of ∠PQR.)
∠XTQ = ∠XSQ (Each 90°)
and QX = QX (Common side)
∴ ∆XTQ ≅ ∆XSQ (By AAS congruence rule)
Then, XT = XS (By CPCT) ........ (1)
Similarly, it can be proved that
∆XSR ≅ ∆XYR (By AAS congruence rule)
Then, XS = XY (By CPCT) ............. (2)
From equations (1) and (2), XT = XY
In right-angled ∆XTP and ∆XYP, we have
XT = XY
∠XTP = ∠XYP (Proved above)
and XP=XP (Each 90°)
∴ ∆XTP ≅ ∆XYP (Common side)
Then, ∠XPT = ∠XPY (By RHS congruence rule)
Therefore, PX bisects ∠P. (By CPCT)
Hence, ∆XTQ = ∆XSQ and PX bisects ∠P.
Hence proved.

Question 2.
ABC is a triangle in which ∠B = 2∠C. D is a point on BC such that AD bisects ∠BAC and AB = CD. Prove that ∠BAC = 72°.
Answer:

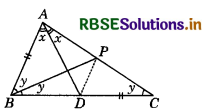
In ∆ABC, given
⇒ ∠B = 2∠C ⇒ ∠B = 2y (Put ∠C = y)
Since, AD is the bisector of ∠BAC.
So, let ∠BAD = ∠CAD = x
Let BP be the bisector of ∠ABC. Join PD.
In ∆ABC, ∠CBP = ∠BCP = y ⇒ PC = BP
(Since, sides opposite to equal angles of a triangle are equal.)
In ∆ABP and ∆DCP,
∠ABP = ∠DCP = y (∵∠ABP = ∠CBP = y and ∠DCP = ∠BCP = y)
AB = DC (Given)
and BP = PC [From equation (1)]
∴ ∆ABP ≅ ∆DCP (By SAS congruence criterion)
⇒ ∠BAP = ∠CDP and AP = DP (By CPCT)
⇒ ∠CDP = 2x (From figure)
and ∠ADP = ∠DAP = x
(Since, angles opposite to equal sides of a triangle are equal.)
In ∆ABD, ∠ADC = ∠ABD + ∠BAD (Since, exterior angle of a triangle is equal to the sum of opposite interior angles.)
⇒ ∠ADP + ∠PDC = ∠ABD + ∠BAD (∵∠ADC = ∠ADP + ∠PDC)
⇒ x + 2x = 2y + x
⇒ x = y ....... (2)
In ∆ABC, ∠A + ∠B + ∠C = 180° (By angle sum property of a triangle)
⇒ 2x + 2y + y = 180°
⇒ 2x + 2x + x = 180° [From equation (2)]
⇒ 5x = 180° ⇒ x = 36°
∴ ∠BAC = 2x = 2 × 36° = 72°
Hence proved.

Question 3.
Show that the sum Of three altitudes of a triangle is less than the sum of the three sides of the triangle.
Answer:

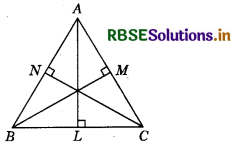
Consider ABC is a triangle and AL, BM and CN are the altitudes.
To prove: AL + BM + CN < AB + BC + AC
Proof: We know that, the perpendicular AL drawn from the point A to the line BC is shorter than the line segment AB drawn from point A to the line BC.
∴ AL < AB
Similarly, BM < BC
and CN < AC
On adding equations (1), (2) and (3), we get :
AL + BM + CN < AB + BC + AC

Question 4.
The image of an object placed at a point A before a plane mirror LM is seen at the point B by an observer at D as shown in figure. Prove that the image is as far behind the mirror as the object is in front of the mirror.

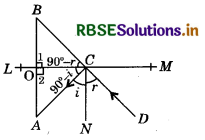
Answer:
In ∆BOC and ∆AOC, we have :
∠1 = ∠2 (Each 90°)
Also, ∠i = ∠r (∵ Incident angle = Reflected angle)
On multiplying both sides by - 1 and then adding 90° both sides, we get:
90° - ∠i = 90° - ∠r
⇒ ∠ACO = ∠BCO
(∵ ∠BCO = 180° - ∠OCN - r = 180° - 90° - r = 90° - r)
and OC = OC (Common side)
∴ ∆BOC ≅ ∆AOC (By ASA congruence rule)
Then, OB = OA (By CPCT)
Hence, the image is as far behind the mirror as the object is in front of the mirror.
Hence proved.

Question 5.
If P is any point in the square ABCD and DPQR is another square, then prove that AP = CR.

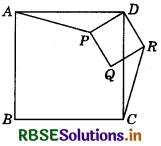
Answer:
Given: P is any point in the square ABCD and DPQR is another square.
To prove: AP = CR
Proof : Let ∠PDC = x°
Then, ∠ADP = ∠ADC - ∠PDC = (90° - x)
and ∠CDR = ∠PDR - ∠PDC = (90° - x)
From equations (1) and (2),
∠ADP = ∠CDR
In ∆ADP and ∆CDR, we have :
AD = CD (Side of a square)
∠ADP = ∠CDR [From equation (3)]
and DP = DR (Sides of a square)
∴ ∆ADP ≅ ∆ CDR (By SAS congruence rule)
Then AP = CR (By CPCT)
Hence proved.