RBSE Class 9 Maths Important Questions Chapter 7 त्रिभुज

Rajasthan Board RBSE Class 9 Maths Important Questions Chapter 7 त्रिभुज Important Questions and Answers.

RBSE Class 9 Maths Chapter 7 Important Questions त्रिभुज

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
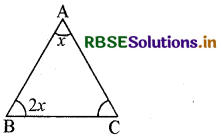
चित्र में AB = AC हो, तो ∠C का मान होगा

(A) 60°
(B) 36°
(C) 72°
(D) 108°
उत्तरः
(C) 72°

प्रश्न 2.
यदि एक त्रिभुज की एक भुजा के मध्य बिन्दु से दूसरी दो भुजाओं पर डाले गए लम्ब समान हों तो त्रिभुज होता है|
(A) समबाहु
(B) समद्विबाहु
(C) समानकोणिक
(D) विषमबाहु
उत्तरः
(B) समद्विबाहु

प्रश्न 3.
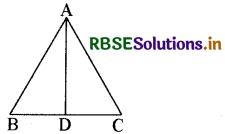
चित्र में ∆ABC में AB = AC एवं AD ⊥ BC हो, तो भुजा AD समद्विभाजक

(A) कोण A की
(B) भुजा BC की
(C) कोण A एवं भुजा BC दोनों की
(D) किसी की भी नहीं
उत्तरः
(C) कोण A एवं भुजा BC दोनों की

प्रश्न 4.
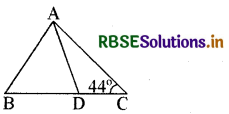
चित्र में प्रदर्शित ∆ABC में AD = BD एवं AC = DC हो एवं ∠C = 44° हो, तो ∠A का मान होगा

(A) 68°
(B) 112°
(C) 34°
(D) 102°
उत्तरः
(D) 102°

प्रश्न 5.
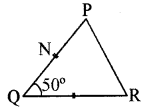
दिये गये चित्र में भुजा PQ = QR। यदि ∠PQR = 50° हो, तो ∠PRQ का माप होगा

(A) 50°
(B) 65°
(C) 100°
(D) 130°
उत्तरः
(B) 65°

प्रश्न 6.
दिए गए चित्र में AB = AC तथा ∠B = 62° तो ∠C का मान है
(A) 62°
(B) 56°
(C) 28°
(D) 310
उत्तरः
(A) 62°

प्रश्न 7.
यदि किसी त्रिभुज के सभी कोण समान हों, तो प्रत्येक कोण का मान होगा-
(A) 90°
(B) 450
(C) 60°
(D) 30°
उत्तरः
(C) 60°

प्रश्न 8.
यदि ∆ABC में, ∠A = 100°, AD ∠A को समद्विभाजित करती है और AD ⊥ BC, तब ∠B =
(A) 50°
(B) 90°
(C) 40°
(D) 100°
उत्तरः
(C) 40°

प्रश्न 9.
यदि ∆ABC में, ∠A = 60°, ∠B = 80° और ∠B तथा ∠C का समद्विभाजक 0 पर मिलता है, तब ∠BOC है-
(A) 60°
(B) 120°
(C) 150°
(D) 30°
उत्तरः
(B) 120°

प्रश्न 10.
रेखाखण्ड AB और CD, O पर प्रतिच्छेदित होते हैं तथा AC || DB, यदि ∠CAB = 45° और ∠CDB = 55°, तब ∠BOD =
(A) 100°
(B) 80°
(C) 90°
(D) 135°
उत्तरः
(B) 80°

प्रश्न 11.
चित्र में यदि AB ⊥ BC, तब x =

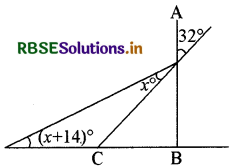
(A) 18
(B) 22
(C) 25
(D) 32
उत्तरः
(B) 22

प्रश्न 12.
चित्र में z का मान x और y के पदों में होगा-

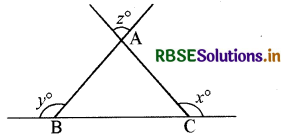
(A) x + y + 180
(B) x + y - 180°
(C) 180° - (x + y)
(D) x + y + 360°
उत्तरः
(B) x + y - 180°

प्रश्न 13.
चित्र में, x के किस मान के लिए l₁ || l₂ होगा-

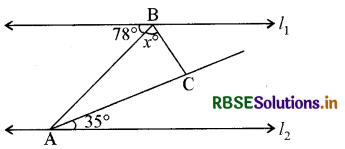
(A) 37
(B) 43
(C) 45
(D) 47
उत्तरः
(D) 47

प्रश्न 14.
चित्र में, यदि l₁ || l₂, तब x का मान होगा-

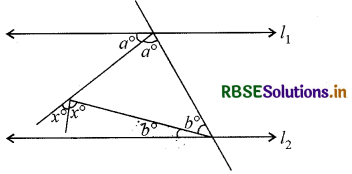
(A) 22½
(B) 30
(C) 45
(D) 60
उत्तरः
(C) 45

प्रश्न 15.
त्रिभुज RST में x का क्या मान होगा-

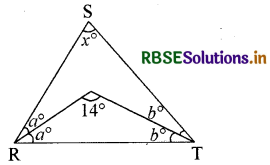
(A) 40°
(B) 90°
(C) 80°
(D) 100°
उत्तरः
(D) 100°

प्रश्न 16.
सर्वांगसम त्रिभुजों ABC व PQR में यदि AB = PQ, BC = QR और ∠A = ∠P । यदि ∠A = 30°, ZB = 70° और ∠C = 80° हों तो ∠Q का मान होगा
(A) 30°
(B) 70°
(C) 800
(D) 110°
उत्तरः
(B) 70°

प्रश्न 17.
एक समद्विबाहु त्रिभुज ABC में AB = AC, ∠BAC का समद्विभाजक AD, BC को बिन्दु D पर मिलता है। यदि ∠BAC = 60° हो तो ∠ADC का मान है-

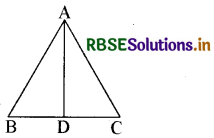
(A) 30°
(B) 60°
(C) 90°
(D) 120°
उत्तरः
(C) 90°

प्रश्न 18.
त्रिभुजों की सर्वांगसमता के लिए निम्न प्रतिबन्ध सही नहीं है-
(A) कोण-कोण-कोण सर्वांगसमता
(B) भुजा-कोण-भुजा सर्वांगसमता
(C) कोण-भुजा-कोण सर्वांगसमता
(D) भुजा-भुजा-भुजा सर्वांगसमता
उत्तरः
(A) कोण-कोण-कोण सर्वांगसमता

प्रश्न 19.
दो त्रिभुजों ABC तथा DEF में AC = DE, BC = EF तथा ∠ABC = ∠DEF = 90° तो दोनों त्रिभुज सर्वांगसम हैं
(A) समकोण-कर्ण-भुजा प्रमेय से
(B) भुजा-कोण-भुजा प्रमेय से
(C) कोण-भुजा-कोण प्रमेय से
(D) भुजा-भुजा-भुजा प्रमेय से
उत्तरः
(A) समकोण-कर्ण-भुजा प्रमेय से

प्रश्न 20.
यदि ∆ABC ≅ ∆LKM तब ∆ABC की भुजा ∆LKM की कौनसी भुजा के बराबर होगी
(A) LK
(B) KM
(C) LM
(D) इनमें से कोई नहीं
उत्तरः
(C) LM

प्रश्न 21.
यदि ∆ABC ≅ ∆PQR और ∆ABC, ∆RPQ के सर्वांगसम नहीं है, तब निम्न में से क्या सही नहीं है?
(A) BC = PQ
(B) AC = PR
(C) AB = PQ
(D) QR = BC
उत्तरः
(A) BC = PQ

प्रश्न 22.
निम्न में से कौनसा विकल्प त्रिभुजों की सर्वांगसमता हेतु नहीं है-
(A) SAS
(B) SSA
(C) ASA
(D) SSS
उत्तरः
(B) SSA

प्रश्न 23.
यदि ∆PQR ≅ ∆EFD, तब ED =
(A) PQ
(B) QR
(C) PR
(D) इनमें से कोई नहीं
उत्तरः
(C) PR

प्रश्न 24.
यदि ∆PQR ≅ ∆EFD, तब ∠E
(A) ∠P
(B) ∠Q
(C) ∠R
(D) इनमें से कोई नहीं
उत्तरः
(A) ∠P

प्रश्न 25.
चित्र में, यदि AC, ∠BAD का समद्विभाजक है ताकि AB = 3 cm और AC = 5 cm, तब CD =

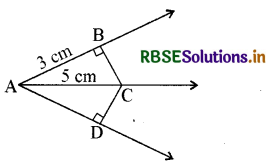
(A) 2 cm
(B) 3 cm
(C) 4 cm
(D) 5 cm
उत्तरः
(C) 4 cm

रिक्त स्थानों की पूर्ति करो

प्रश्न 1.
यदि किसी त्रिभुज की दो भुजाएँ बराबर हों, तो उनके सम्मुख कोण ................ होते हैं।
उत्तरः
बराबर

प्रश्न 2.
समान त्रिज्याओं वाले दो वृत्त ................ होते
उत्तरः
सर्वांगसम

प्रश्न 3.
किसी समबाहु त्रिभुज का प्रत्येक कोण ................ का होता है।
उत्तरः
60°

प्रश्न 4.
जब दो राशियाँ असमान होती हैं, उस समय दोनों राशियों की तुलना करने पर राशियों के मध्य जो सम्बन्ध बनता है, वह ........................ सम्बन्ध कहलाता है।
उत्तरः
असमिका

प्रश्न 5.
किसी त्रिभुज की दो भुजाओं का योग तीसरी भुजा से ................. होता है।
उत्तरः
बड़ा

प्रश्न 6.
किसी त्रिभुज में बड़ी भुजा का सम्मुख कोण .............. होता है।
उत्तरः
बड़ा

प्रश्न 7.
यदि ∆PQR = ∆EFD, तब ED =
उत्तरः
PR

प्रश्न 8.
यदि ∆PQR = ∆EFD, तब ∠E =
उत्तरः
∠P

सत्य/असत्य-निम्नलिखित कथनों के लिए सत्य अथवा असत्य लिखिए

प्रश्न 1.
यदि दो त्रिभुजों में से एक त्रिभुज की दो भुजाएँ दूसरे त्रिभुज की दो भुजाओं के अलग-अलग हों और इनके बीच के कोण भी आपस में बराबर हों तो दोनों त्रिभुज सर्वांगसम होंगे।
उत्तर:
सत्य

प्रश्न 2.
यदि किसी त्रिभुज के दो कोण बराबर हों, तो उनके सामने की भुजाएँ बराबर नहीं हो सकतीं।
उत्तर:
असत्य

प्रश्न 3.
यदि दो समकोण त्रिभुजों में कर्ण बराबर हों, तो त्रिभुज सदैव सर्वांगसम होते हैं।
उत्तर:
असत्य

प्रश्न 4.
किसी त्रिभुज की दो भुजाओं का योग तीसरी भुजा से बड़ा होता है।
उत्तर:
सत्य

प्रश्न 5.
किसी बाह्य बिन्दु से दी हुई सरल रेखा तक खींची गई समस्त रेखाओं में लम्ब ही सबसे बड़ा होता है।
उत्तर:
असत्य

प्रश्न 6.
किसी भी त्रिभुज में बड़े कोण की सम्मुख भुजा छोटे कोण की सम्मुख भुजा से बड़ी होती है।
उत्तर:
सत्य

प्रश्न 7.
यदि किसी त्रिभुज के कोण 2 : 4 : 3 के अनुपात में हों तो सबसे छोटे कोण का माप 40° है।
उत्तर:
सत्य

प्रश्न 8.
यदि किसी त्रिभुज में कोणों का अनुपात 5 : 3 : 7 हो तो त्रिभुज समकोण त्रिभुज होगा।
उत्तर:
असत्य

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
समबाहु त्रिभुज के प्रत्येक कोण का मान लिखिए।
हल:
प्रत्येक कोण \(\frac{180}{3}\) = 60° होगा।

प्रश्न 2.
किसी त्रिभुज की बराबर भुजाओं के सम्मुख कोण कैसे होते हैं ?
हल:
बराबर भुजाओं के सम्मुख कोण समान होते हैं।

प्रश्न 3.
चित्र के अनुसार ∆ ABC में AB = AC; CD = CA एवं ∠ADC = 20° हो, तो ∠ABC का मान ज्ञात कीजिए।

हल:
∆∆BC में
AB = AC अत: ∠B = ∠C होगा
इसी प्रकार ∆ ACD में
CD = CA अत: ∠∆ = ∠D
अत: ∆ ACD में
∠C = 180° - 2 × 20 = 140°
∆ABC में
∠C = 180° - 140° = 40°
∵ ∠ABC = ∠ACB
अतः ∠∆BC = 40° होगा।

प्रश्न 4.
∆ ABC एवं ∆ DEF में यदि AB = DE, BC = DE, AC = EF एवं ∠D = 55° हो, तो ∠B का मान ज्ञात कीजिए।
हल:
यहाँ ∆ ABC व ∆ DEF में

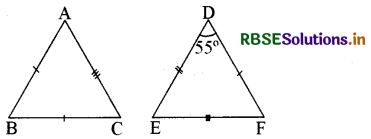
AB = DF
BC = DE
AC = EF
अतः ∆ABC ≅ ∆ DEF
अतः ∠D = ∠B = 55° होगा।

प्रश्न 5.
चित्र में ∠B = ∠D = 90° हैं, तथा BC = CD हो, तो क्या AB = DE है? क्यों?

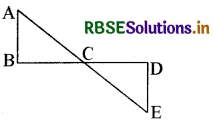
हल:
∆ ABC व ∆ CDE में।
∠B = ∠D = 90° (दिया है)
BC = CD भुजा के (दिया है)
∠BCA = ∠DCE (सम्मुख कोण)
अत: ∆ ABC ≅ ∆ CDE के (ASA नियम से)
अतः AB = DE होगा

प्रश्न 6.
दिए गए चित्र में ∠1 = ∠2 तथा ∠3 = ∠4 तो बराबर भुजाएँ कौन-कौनसी हैं?

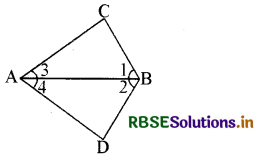
हल:
AC = AD तथा BC = BD होंगी।

प्रश्न 7.
नीचे दी गई आकृति में AB = AC तो ∠C का मान अंशों में लिखिए।

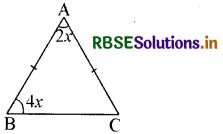
हल:
4x + 2x + 4x = 180
10x = 180
या x = \(\frac{180}{10}\) = 18°
अतः ∠C = 4 × 18 = 72°

प्रश्न 8.
यदि ∆ABC में AB = AC हो तथा ∠A < 60° हो, तो भुजा BC एवं AC में सम्बन्ध लिखिए।
हल:
यहाँ ∆ABC में AB = AC
∴ ∠C = ∠B
तथा ∠A < 60°
∴ ∠B व ∠C बराबर और 60° से बड़े कोण होंगे
∵ BC के सामने का ∠A < 60° और AC के सामने का ∠B > 60°
अतः BC < AC

प्रश्न 9.
दिये गये चित्र में भुजा AB एवं AC में संबंध लिखिए।

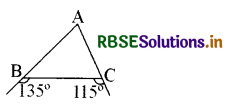
हल:
चित्रानुसार बहिष्कोण B = 135°
(AB भुजा को बढ़ाने पर बनने वाला कोण)
∴ ∠ABC = 180° - 135° = 45°
तथा C बिन्दु पर बहिष्कोण = 1150
∴ ∠ACB = 180° - 115° = 65°
यहाँ ∠B = 45°, ∠C = 65° व ∠A = 70°
अर्थात् ∠ACB > ∠ABC
या AB > AC.
(कोणों की सम्मुख भुजाएँ)

प्रश्न 10.
किसी त्रिभुज ABC में ∠A > ∠B एवं ∠B > ∠C हो, तो सबसे छोटी भुजा होगी
हल:
यहाँ ∠C सबसे छोटा है अतः इसके सामने की भुजा AB सबसे छोटी होगी।

प्रश्न 11.
चित्र में यदि AB = AC हो, तो भुजा AB एवं AD में सम्बन्ध लिखिए।

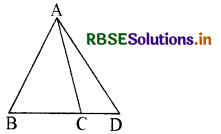
हल:
∆ ABC में ∠C बहिष्कोण है
जो ∠B + ∠BAC के समान है।
अतः ∠ACD > ∠B or ∠A
अतः भुजा AD > AB

प्रश्न 12.
दिये गये चित्र में AB = 6 सेमी., BC = 7 सेमी. तथा AC = 6.9 सेमी. हों तो लिखिए

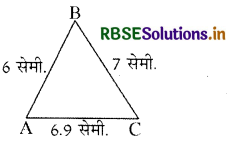
(i) त्रिभुज का सबसे बडा कोण
(ii) त्रिभुज का सबसे छोटा कोण।
उत्तर:
(i) त्रिभुज का सबसे बड़ा कोण = ∠CAB
(ii) त्रिभुज का सबसे छोटा कोण = ∠ACB

प्रश्न 13.
दिए गए चित्र में ∠Y = 80° तथा ∠Z = 60° हो तो लिखिए
(i) त्रिभुज की सबसे बड़ी भुजा।
(ii) त्रिभुज की सबसे छोटी भुजा।

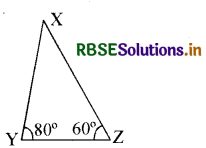
उत्तर:
(i) सबसे बड़ी भुजा XZ
(ii) संबसे छोटी भुजा YZ

प्रश्न 14.
चित्र में AB = AC एवं ∠B = 58° हो तो ∠A का मान ज्ञात कीजिए
हल:

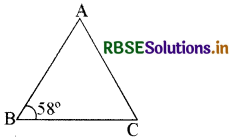
∆ ABC में AB = AC अतः
∠B = ∠C होगा।
∆ के तीनों कोणों का योग = 180°
अतः ∠A + ∠B + ∠C = 180°
∠A + 58° + 58° = 180°
∠A = 180° – 116
= 64°

लघूत्तरात्मक प्रश्न

प्रश्न 1.
चित्र में ∠B > ∠A एवं ∠D > ∠E हो, तो सिद्ध कीजिए कि

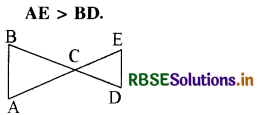
हल:
∆ ABC में ∠B > ∠A है
अतः भुजा AC > BC .............. (i)
इसी प्रकार ∆ CED में।
∠D > ∠E
अतः भुजा CE > DC ............... (ii)
समीकरण (i) व (ii) से
AC + CE > BC + DC
या AE > BD

प्रश्न 2.
किसी त्रिभुज ABC में AB > AC एवं भुजा BC पर कोई बिन्दु D हो, तो सिद्ध कीजिए

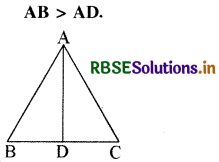
हल:
यहाँ AB > AC दिया है
अब ∆ ABD में ∠ADB, ∆ ADC के ∠D का बहिष्कोण है।
अतः ∠ADB > ∠C
या ∠ADB > ∠B << ∠C
∵ ∠B < ∠C इस प्रकार ∆ABD में ∠ADB > ∠B
अतः भुजा AB > AD

प्रश्न 3.
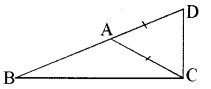
चित्र में AD = BD एवं ∠C = ∠E हो, तो सिद्ध कीजिए BC = AE

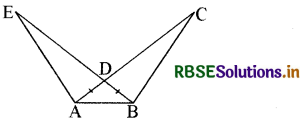
हल:
∆ ABE तथा ∆ ABC में
∠E = ∠C दिया है।
∠ABE = ∠CAB के
(∵ AD = BD अत: ∆ ABD में ∠A = ∠B)
AB भुजा उभयनिष्ठ है।
अत: ∆ABE ≅ ∆ABC
अतः BC = AE होगा।

प्रश्न 4.
यदि एक समद्विबाहु त्रिभुज ABC की माध्यिका AD हो तथा ∠A = 120° एवं AB = AC हो, तो ∠ADB का मान ज्ञात कीजिए।

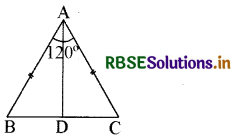
हल:
AB = AC
अतः ∠B = ∠C
∠B + ∠C = 180° - 120° = 60°
अतः ∠B = ∠C = 30°
∠ADB = 180° - (60° + 30°)
∠ADB = 180° - 90° = 90°

प्रश्न 5.
यदि त्रिभुज के किसी कोण का समद्विभाजक सम्मुख भुजा को भी समद्विभाजित करता है, तो सिद्ध कीजिए कि त्रिभुज समद्विबाहु होगा।
हल:
यहाँ ∆ ABC में ∠A का समद्विभाजक AD भुजा BC को समद्विभाजित करता है

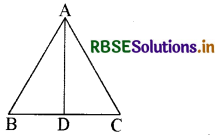
अतः BD = CD
∆ ABD व ∆ ADC में
∠BAD = ∠DAC (दिया हुआ है।)
भुजा BD = CD (दिया हुआ है।)
AD उभयनिष्ठ है अतः
∆ ABD ≅ ∠ADC a
अतः AB = AC
अतः यह समद्विबाहु D होगा।

प्रश्न 6.
दी गई आकृति में OA = OB और OD = OC है। दर्शाइए कि

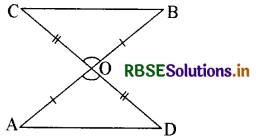
(i) ∆ AOD ≅ D BOC और.
(ii) AD || BC है।
हल:
(i) ∆ AOD और ∆ BOC में,

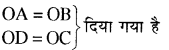
साथ ही, ∵ ∠AOD और ∠BOC शीर्षाभिमुख कोणों का एक युग्म है, अत:
∠AOD = ∠BOC
∴ ∆ AOD ≅ ∆ BOC
(SAS सर्वांगसमता नियम से)

(ii) सर्वांगसम त्रिभुजों AOD और BOD में, अन्य संगत भाग भी बराबर होंगे।
अतः ∠OAD = ∠OBC है परन्तु ये रेखाखण्डों AD और BC के लिए एकान्तर कोणों का एक युग्म बनाते हैं।
अत: AD || BC है।

प्रश्न 7.
AB एक रेखाखण्ड है और रेखा । इसका लम्ब समद्विभाजक है। यदि। पर स्थित P कोई बिन्द है, तो दर्शाइए कि P बिन्दुओं A और B से समदूरस्थ (equidistant) है।
हल:
l ⊥ AB है और AB के मध्य बिन्द C से होकर जाती है जैसा आकृति में दिखाया गया है। यहाँ पर हमको सिद्ध करना होगा कि PA = PB है। इसके लिए ∆ PCA और ∆ PCB पर हम विचार करेंगे।

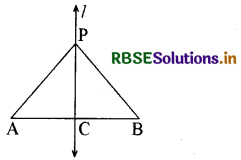
AC = BC
(C, AB का मध्य बिन्द है)
∠PCA = ∠PCB = 90° दिया है
PC = PC (उभयनिष्ठ)
अतः ∆ PCA ≅ ∆ PCB (SAS नियम)
∴ PA = PB.
(सर्वांगसम त्रिभुजों की संगत भुजायें)

प्रश्न 8.
रेखाखण्ड AB एक अन्य रेखाखण्ड CD के समान्तर है और 0 रेखाखण्ड AD का मध्य बिन्दु है। (आकृति में देखिये) सिद्ध कीजिए कि

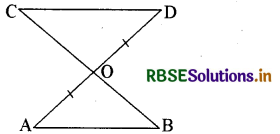
(i) ∆ AOB ≅ ∆ DOC
(ii) 0 रेखाखण्ड BC का भी मध्य-बिन्द है।
हल:
(i) हम यहाँ पर ∆AOB और ∆ DOC पर विचार करेंगे
∠ABO = ∠DCO
(एकान्तर कोण और तिर्यक रेखा BC के साथ | AB || CD)
∠AOB = ∠DOC (शीर्षाभिमुख कोण)
OA = OD दिया है।
अतः ∆ AOB ≅ ∆ DOC (AAS नियम)
(ii) OB = OC (CPCT)
अर्थात् O रेखाखण्ड BC का भी मध्य-बिन्दु है।

प्रश्न 9.
∆ ABC में, ∠A का समद्विभाजक AD भुजा BC पर लम्ब है (देखिये आकृति) दर्शाइए कि AB = AC है और ∆ ABC समद्विबाहु है।

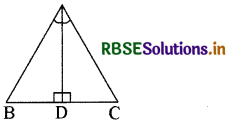
हल:
∆ ABD और ACD में
∠BAD = ∠CAD (दिया है)
AD = AD (उभयनिष्ठ)
∠ADB = ∠ADC = 90° (दिया है)
अतः ∆ ABD ≅ ∆ ACD (ASA नियम)
∴ AB = AC (CPCT)
इसी कारण ∆ ABC समद्विबाहु है।

प्रश्न 10.
E और F क्रमशः त्रिभुज ABC की बराबर भुजाओं AB तथा AC के मध्य-बिन्दु हैं। ( देखिये आकृति ) दर्शाइए कि BF = CE है।

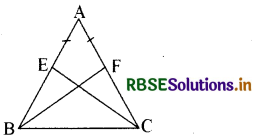
हल:
∆ ABF और ∆ ACE में,
AB = AC (दिया है)
∠A = ∠A (उभयनिष्ठ)
AF = AE (बराबर भुजाओं के आधे)
अत: ∆ABF ≅ ∆ ACE (SAS नियम)
∴ BF = CE (CPCT)

प्रश्न 11.
एक समद्विबाहु त्रिभुज ABC जिसमें AB = AC है, की भुजा BC पर दो बिन्दु D और E इस प्रकार हैं कि BE = CD है ( देखिए आकृति)। दर्शाइए कि AD = AE है।

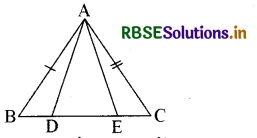
हल:
∆ ABD और ∆ ACE में,
AB = AC (दिया है) .....(1)
∠B = ∠C .....(2)
(बराबर भुजाओं के सम्मुख कोण)
साथ ही, BE = CD (दिया है)
इसलिए, BE - DE = CD - DE
अर्थात्, BD = CE .....(3)
अतः, ∆ ABD ≅ ∆ ACE
[(1), (2), (3) और SAS नियम द्वारा]
इससे प्राप्त होता है-AD = AE (CPCT)

प्रश्न 12.
∆ ABC की भुजा BC पर D एक ऐसा बिन्दु है कि AD = AC है ( देखिए आकृति)। दर्शाइए कि AB > AD है।

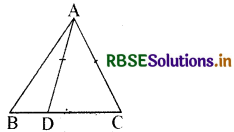
हल:
∆ DAC में,
AD = AC (दिया है)
इसलिए, ∠ADC = ∠ACD
(बराबर भुजाओं के सम्मुख कोण)
अब, ∠ADC त्रिभुज ABD का एक बहिष्कोण है|
इसलिए, ∠ADC > ∠ ABD
या, ∠ACD > ∠ ABD
या, ∠ACB > ∠ ABC
अतः, AB > AC
(∆ ABC में बड़े कोण की सम्मुख भुजा)
या, AB > AD (AD = AC)

प्रश्न 13.
ABC एक त्रिभुज है जिसमें AB = AC,
(i) यदि ∠A < 60° तो सिद्ध कीजिए कि BC < AB. (ii) यदि ZA > 60° तो सिद्ध कीजिए कि BC > AB

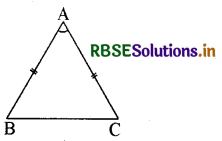
हल:
(i) ∆ ABC में AB = AC
अत: ∠B = ∠C होगा यदि
∠A < 60° तो ∠B व ∠C का मान ∠A से अधिक होगा अतः BC < AB (ii) यदि ∠A > 60° तो ∠C व ∠B का मान ∠A से कम होगा।
अतः BC > AB

प्रश्न 14.
दो समकोण त्रिभुजों में एक त्रिभुज की एक भुजा और एक न्यून कोण दूसरे त्रिभुज की एक भुजा तथा संगत न्यूनकोण के बराबर है। सिद्ध कीजिए कि दोनों त्रिभुज सर्वांगसम हैं।

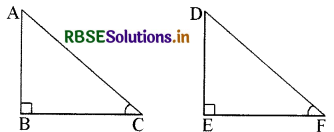
हल:
माना कि दो समकोण त्रिभुज ABC और DEF हैं जिनमें ∠B तथा E पर समकोण है, भुजा AB = DE तथा ∠C = ∠F है।
अब हमें सिद्ध करना है कि ∆ ABC ≅ ∆ DEL.
अब ∆ABC और ∆ DEF से
∠B = ∠E [प्रत्येक कोण 90°]
∠C ≅ ∠F (दिया है)
AB = DE (दिया है)
अतः ∆ ABC ≅ ∆ DEF
[सर्वांगसमता के AAS नियम के अनुसार]
अतः दिये गए दोनों त्रिभुज सर्वांगसम हैं।

प्रश्न 15.
ABCD एक वर्ग है। भुजाओं AD और BC पर क्रमश: X और Y ऐसे बिन्दु हैं कि AY = BX तो सिद्ध कीजिए कि BY = AX और ∠BAY = ∠ABX.
हल:
प्रश्नानुसार हमें दिया गया है कि वर्ग की भुजाओं AD और BC पर क्रमशः बिन्दु X और Y इस प्रकार हैं कि AY = BX.
हम जानते हैं कि किसी भी वर्ग की आसन्न भुजाएँ परस्पर लम्बवत् होती हैं।

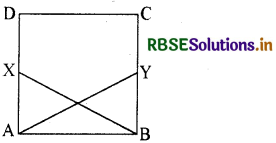
∴ ∠A = ∠B = 90°
समकोण ∆ABY तथा ∆ BAX में
∠A = ∠B = 90° (दिया है)
AY = BX (दिया है)
AB = AB (उभयनिष्ठ भुजा)
अतः ∆ ABY ≅ ∆ BAX
(सर्वांगसमता के RHS नियम के अनुसार)
⇒ BY = AX
तथा ∠BAY = ∠ABX
(क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं।)

निबन्धात्मक प्रश्न

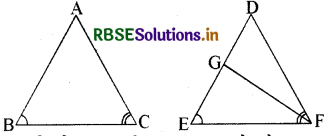
प्रश्न 1.
नीचे दी हुई आकृतियों में ∆ ABC की दो भुजाएँ AB, BC और माध्यिका AD क्रमशः ∆ PQR की भुजाओं PQ, QR और माध्यिका PM बराबर हैं। सिद्ध कीजिए कि ∆ ABC ≅ ∆ PQR

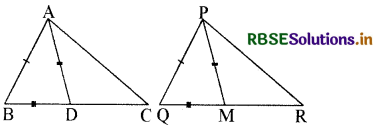
हल:
उपपत्ति- ∆ ABD तथा ∆ PQM में

∵ \(\frac{\mathrm{BC}}{2} = \frac{\mathrm{QR}}{2}\) या BC = QM
अतः SSS प्रमेय द्वारा
∆ ABD ≅ ∆ PQM
अतः ∠B = ∠Q
अब पुन: ∆ ABC एवं ∆ PQR में
∠B = ∠Q
BC = QR
AB = PQ
SAS प्रमेय से
∆ ABC ≅ ∆ PQR

प्रश्न 2.
सिद्ध कीजिए कि त्रिभुज की तीनों भुजाओं का योग उसकी तीनों माध्यिकाओं के योग से अधिक होता है।
हल:
दिया है: ∆ ABC जिसकी माध्यिकाएँ AD, BE व CF हैं
सिद्ध करना है: AB + BC + AC > AD + BE + CF
रचना: AD को G तक इस प्रकार बढ़ाया कि DG = AD हो एवं CG को मिलाया।

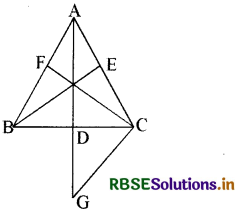
उपपत्ति: ∆ ADB एवं ∆ GDC में
AD = DG (रचना से)
BD = DC (दिया हुआ है)
∠ADB = ∠GDC (शीर्षाभिमुख कोण)
अतः ∆ ADB ≅ ∆ GDC (भुजा-कोण-भुजा प्रमेय)
अतः AB = CG
∆ ACG में AC + CG > AG
⇒ AC + AB > AG(∵ CG = AB)
⇒ AC + AB > 2 AD (∵ AG = 2 AD).....(i)
इसी प्रकार AC + BC > 2 CF .....(ii)
तथा AB + BC > 2 BE .....(iii)
समीकरण (i), (ii) तथा (iii) को जोड़ने पर
अतः 2 (AB + BC + AC) > 2 (AD + BE + CF)
या AB + BC + AC > AD + BE + CF

प्रश्न 3.
चित्र में त्रिभुज में कोई अन्तः बिन्दु O हो, तो सिद्ध कीजिए कि
(BC + AB + AC) < 2 (OA + OB + OC)

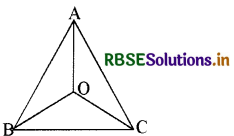
हल:
दिया है-एक ∆ ABC है जिसमें 0 एक अन्तः बिन्दु है।
सिद्ध करना है-(BC + AB + AC) < 2 (OA + OB + OC) उपपत्ति-∆ AOB में, OA + OB > AB .....(i)
∆BOC में, OB + OC > BC .....(ii)
∆AOC में, OA + OC > AC .....(iii)
समीकरण (i), (ii) व (iii) को जोड़ने पर
(OA + OB) + (OB + OC) + (OA + OC) >AB + BC + AC
⇒ 2 (OA + OB + OC) > AB + BC + AC
या AB + BC + AC < 2 (OA + OB + OC) प्रश्न 4. सिद्ध कीजिए कि त्रिभुजों के तीनों शीर्ष लम्बों का योग त्रिभुज के परिमाप से कम होता है। हल: दिया है-∆ ABC जिसमें A, B तथा C से BC, AC व AB पर डाले गये लम्ब क्रमशः AD, BE तथा CF हैं। सिद्ध करना है- AB + BC + CA > AD + BE + CF

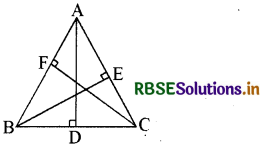
उपपत्ति- ∆ ADB में
∠ADB = 90°
अतः AB > AD ............... (i)
इसी प्रकार ∆ BEC में
BE ⊥ AC
अतः BC > BE .............(ii)
∆ CAF में CF ⊥ AB
अतः AC > CF ............. (iii)
(i), (ii) व (iii) को जोड़ने पर
AB + BC + CA> AD + BE + CF

प्रश्न 5.
सिद्ध कीजिए कि किसी त्रिभुज की दो भुजाओं का अन्तर तीसरी भुजा से छोटा होता है।
हल:
सिद्ध करना है कि BA > BC - AC
रचना-एक त्रिभुज ABC है। BA को D तक इस प्रकार आगे बढ़ाओ कि AD = AC हो।

व्याख्या-
∵ AD = AC
∴ ∠ACD = ∠ADC
(बराबर भुजाओं के सामने के कोण)
∴ ∠BCD > ∠ADC
BD > BC (बड़े कोण के सामने की भुजा)
BA + AD > BC
BA + AC > BC
BA > BC ∠AC (इति सिद्धम् )

प्रश्न 6.
चित्र में ∆ ABC के अन्दर कोई बिन्दु 0 हो तो सिद्ध कीजिए कि
AB + AC > OB + OC

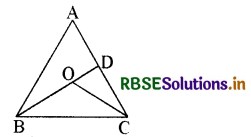
हल:
दिया है-∆ ABC में O एक अन्तः बिन्दु है।
सिद्ध करना है- AB + AC > OB + OC
रचना-BO को आगे बढ़ाया जो AC को D पर मिलती है।
उपपत्ति-हम जानते हैं कि त्रिभुज में किन्हीं दो भुजाओं का योग तीसरी भुजा से अधिक होता है।
अत: ∆ ABD में
AB + AD > BD
⇒ AB + AD > OB + OD ........... (1)
इसी प्रकार ∆ OCD में
OD + DC > OC ..............(2)
(1) व (2) का योग करने पर
AB + AD + OD + DC > OB + OD + OC
⇒ AB + (AD + DC) > OB + OC
⇒ AB + AC > OB + OC

प्रश्न 7.
यदि ABCD एक चतुर्भुज हो तो सिद्ध कीजिए कि

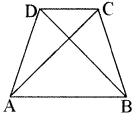
(i) AB + BC + CD + DA > 2 AC
(ii) AB + BC + CD + DA > AC + BD
हल:
दिया है-चतुर्भुज ABCD
सिद्ध करना है
(i) AB + BC + CD + DA > 2 AC
(ii) AB + BC + CD + DA > AC + BD
रचना- विकर्ण AC एवं BD को मिलाया।
उपपत्ति- हम जानते हैं कि किसी त्रिभुज की दो भुजाओं का योग तीसरी भुजा से अधिक होता है अतः
∆ABC में AB + BC > AC .....(i)
∆ADC में AD + DC > AC .....(ii)
∆ABD में AB + AD > BD .....(iii)
∆BCD में BC + CD > BD .....(iv)
(i) व (ii) का योग करने पर AB + BC + AD + CD > 2 AC (इति सिद्धम्)
पुनः (i), (ii), (iii) व (iv) का योग करने पर
2 (AB + BC + AD + DC)> 2 (AC + BD)
⇒ AB + BC + AD + DC > AC + BD (इति सिद्धम् )

प्रश्न 8.
सिद्ध करो कि यदि एक त्रिभुज के कोई दो कोण और उनकी अंतरित भुजा दूसरे त्रिभुज के दो कोणों और उनकी अंतरित भुजा के बराबर हो, तो दोनों त्रिभुज सर्वांगसम होते हैं।
हल:
दिया है-ABC एवं DEF दो त्रिभुज हैं, जहाँ ∠ ABC = ∠ DEE, ∠ACB = ∠ DFE एवं BC = EF है।
सिद्ध करना है-∆ABC ≅ ∆ DEF
उपपत्ति: यहाँ दोनों त्रिभुजों ABC एवं DEF की भुजा AB एवं DE की लम्बाई की तुलना करने पर निम्न तीन स्थितियाँ सम्भव हैं
(i) AB = DE
(ii) AB < DE एवं (iii) AB > DE

स्थिति (i)-यदि ∆B = DE हो, तो ∆ ∆BC एवं ∆ DEF में
AB = DE (माना)
∠ABC = ∠DEF (दिया है)
BC = EF (दिया है)
अतः ∆ ∆BC एवं ∆ DEF भुजा-कोण-भुजा गुणधर्म से सर्वांगसम है।
अर्थात् ∆ABC ≅ ∆ DEF.
स्थिति (ii)- यदि AB < DE हो, तो भुजा DE पर एक बिन्दु G इस प्रकार लिया कि AB = GE एवं GF को मिलाया।
अब ∆ ABC एवं GEF के लिए
AB = GE (माना)
BC = EF (दिया है)
∠ABC = ∠GEF (दिया है)
[∵ ∠GEF = ∠DEF]
अर्थात् भुजा-कोण-भुजा गुणधर्म से ∆ABC = ∆GEFअतः
∠ACB = ∠GEF एवं ∠ACB = ∠DFE (दिया है)....(ii)(i) व (ii) से ∠DFE = ∠GFE
जो तब तक असंभव है, जब तक कि GF, DF के साथ संपाती न हो जाए अर्थात् G एवं D संपाती हैं।
∴ AB = DE अतः भुजा-कोण-भुजा गुणधर्म से ∆ ABC ≅ ∆ DEF
स्थिति (iii): यदि AB > DE हो तो निम्न चित्रानुसार ∆ ABC में भुजा AB पर एक बिन्दु G इस प्रकार लिया कि BG = DE हो।
यहाँ स्थिति (ii) के अनुसार हम सिद्ध कर सकते हैं कि बिन्दु G, बिन्दु ∆ के संपाती होगा अर्थात् AB = DE और भुजा-कोण-भुजा गुणधर्म से
∆ ABC ≅ ∆ DEF

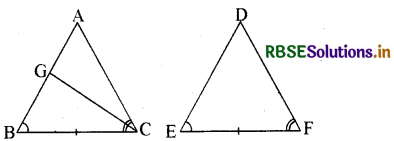
∴ सभी तीनों स्थितियों में ∆ABC ≅ ∆ DEF (इति सिद्धम्)

प्रश्न 9.
AB एक रेखाखण्ड है तथा बिन्दु P तथा 0 इस रेखाखण्ड AB के विपरीत ओर इस प्रकार स्थित हैं कि इनमें से प्रत्येक A और B से समदूरस्थ है ( देखिये आकृति) दर्शाइए कि रेखा PO रेखाखण्ड AB का लम्ब समद्विभाजक है।

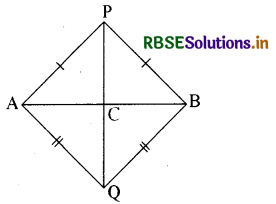
हल:
दिया गया है
PA = PB और QA = QB
हमको सिद्ध करना है कि PQ ⊥ AB है।
और PQ रेखाखण्ड AB को समद्विभाजित करता है। माना रेखा PQ रेखाखण्ड AB को C पर प्रतिच्छेद करती है।
∆ PAQ और ∆ PBQ में
AP = BP दिया है
AQ = BQ दिया है
PQ = PQ उभयनिष्ठ
अतः ∆ PAQ ≅ ∆ PBQ (SSS नियम से)
∴∠APQ = ∠ BPQ (CPCT)
अब ∆ PAC और ∆ PBC को लेते हैं।
AP = BP दिया है
∠APC = ∠ BPC
∠APQ = ∠ BPQ ऊपर सिद्ध किया है
PC = PC (उभयनिष्ठ)
अतः ∆ PAC ≅ ∆ PBC (SAS नियम)
∴ AC = BC (CPCT) .......(1)
और ∠ACP = ∠BCP (CPCT)
∴ साथ ही ∠ ACP + ∠ BCP = 180° (युग्मरैखिक)
∴ 2 ∠ACP = 180°
या ∠ACP = \(\frac{180^{\circ}}{2}\)
∠ACP = 90° ....... (2)
समीकरण (1) तथा (2) से निष्कर्ष निकाल सकते हैं कि रेखा PQ रेखाखण्ड AB का लम्ब समद्विभाजक है।

प्रश्न 10.
बिन्दु A पर प्रतिच्छेद करने वाली दो रेखाओं l और m से समदूरस्थ एक बिन्दु P है। (देखिये आकृति में)
सिद्ध कीजिए कि रेखा AP दोनों रेखाओं के बीच के कोण को समद्विभाजित करती है।

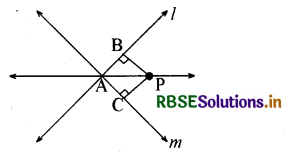
हल:
दिया गया है कि रेखायें ! और m परस्पर A क) | पर प्रतिच्छेद करती हैं।
माना PB ⊥ l
और PC ⊥ m हैं।
यह दिया है कि PB = PC है।
सिद्ध करना है कि
∠PAB = ∠ PAC है।
अब ∆ PAB और ∆ PAC में,
PB = PC (दिया है)
∠PBA = ∠PCA = 90° (दिया है)
PA = PA (उभयनिष्ठ)
अतः ∆ PAB ≅ ∆ PAC (RHS नियम)
∴ ∠PAB = ∠PAC (CPCT) (इति सिद्धम्)