RBSE Class 9 Maths Important Questions Chapter 6 Lines and Angles

Rajasthan Board RBSE Class 9 Maths Important Questions Chapter 6 Lines and Angles Important Questions and Answers.

RBSE Class 9 Maths Chapter 6 Important Questions Lines and Angles

I. Multiple Choice Questions:
Choose the correct answer from the given four options.

Question 1.
In the given figure AOB is a straight line. If ∠AOC + ∠BOD = 95°, then ∠COD = ?

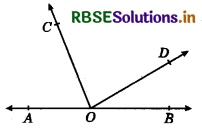
(a) 95°
(b) 85°
(c) 90°
(d) 55°
Answer:
(b) 85°

Question 2.
In the adjoining figure, AOB is a straight line: If x : y : z = 4 : 5 : 6, then y = ?

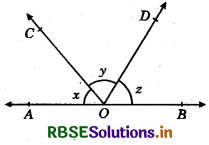
(a) 60°
(b) 80°
(c) 48°
(d) 72°
Answer:
(a) 60°

Question 3.
An exterior angle of a triangle is 105° and its two interior opposite angles are equal. Each of the equal angle is :
(a) 37\(\frac{1^{\circ}}{2}\)
(b) 52\(\frac{1^{\circ}}{2}\)
(c) 72\(\frac{1^{\circ}}{2}\)
(d) 75°
Answer:
(b) 52\(\frac{1^{\circ}}{2}\)

Question 4.
In the adjoining figure if m ∥ n, then the value of x is:

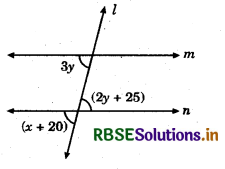
(a) 60°
(b) 55°
(c) 50°
(d) 45°
Answer:
(b) 55°

Question 5.
In the adjoining figure AB ∥ CD ∥ EF and PQ ∥ RS. If ∠CQP = 60° and ∠RQD = 25° then ∠QRS is equal to:

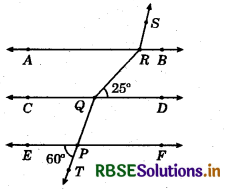
(a) 85°
(b) 135°
(c) 145°
(d) 110°
Answer:
(c) 145°

Question 6.
In the given figure straight lines AB and CD intersect at O. If ∠AOC = Φ, ∠BOC = θ and θ = 3Φ, then=?

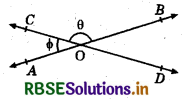
(a) 30°
(b) 40°
(c) 45°
(d) 60°
Answer:
(c) 45°

Question 7.
In the given figure AB ∥ CD, if ∠ABO = 130° and ∠OCD = 1100, then ∠BOC =?

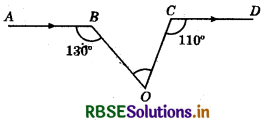
(a) 50°
(b) 60°
(c) 70°
(d) 80°
Answer:
(b) 60°

Question 8.
In the given figure AB ∥ CD, if ∠AOC = 30° and ∠OAB = 100°, then ∠OCD = ?

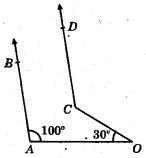
(a) 130°
(b) 150°
(c) 80°
(d) 100°
Answer:
(a) 130°

Question 9.
In the given figure AB ∥ CD. If ∠CAB = 80° and ∠EFC = 25°, then ∠CEF = ?

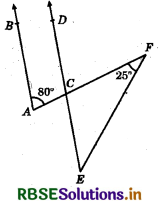
(a) 65°
(b) 55°
(c) 45°
(d) 75°
Answer:
(b) 55°

Question 10.
In the given figure, AOB is a straight line. If ∠AOC = (∠x - 10), ∠COD = 50° and ∠BOD = (∠C + 20), then ∠AOC = ?

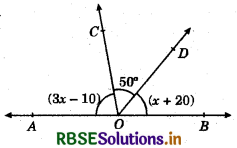
(a) 40°
(b) 60°
(c) 80°
(d) 50°
Answer:
(c) 80°

Question 11.
In ΔABC, side BC is produced to D. If ∠ABC = 40° and ∠ACZ = 120° then ∠A= ?

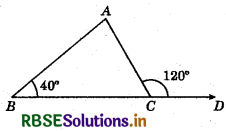
(a) 60°
(b) 40°
(c) 80°
(d) 50°
Answer:
(c) 80°

Question 12.
In the given figure BO and CO are the bisectors of ∠B and ∠C respectively. If ∠A = 50°, then ∠BOC = ?

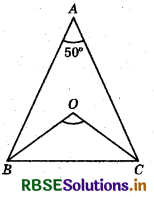
(a) 130°
(b) 100°
(c) 115°
(d) 120°
Answer:
(c) 115°

Question 13.
In the given figure if ∠OAB = 75°, ∠OBA = 55° and ∠OCD = 100°, then ∠ODC =?

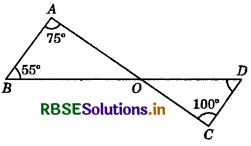
(a) 20°
(b) 25°
(c) 30°
(d)35°
Answer:
(c) 30°

Question 14.
In the given figure ∠BAC = 30°, ∠ABC = 50° and ∠CDE = 40°. Then ∠AED=?

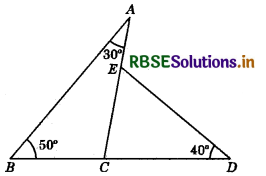
(a) 120°
(b) 100°
(c) 80°
(d) 110°
Answer:
(a) 120°

Question 15.
In the given figure AB ∥ CD. If ∠APQ = 70° and ∠PRD = 120°,then ∠QPR=? ;

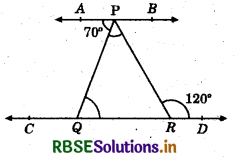
(a) 50°
(b) 60°
(c) 40°
(d) 35°
Answer:
(a) 50°

Question 16.
In the given figure, if l ∥ m then x is equal to:

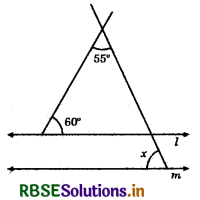
(a) 55°
(b) 65°
(c) 75°
(d) 115°
Answer:
(b) 65°

Question 17.
For what values of x shall we have l ∥ m?

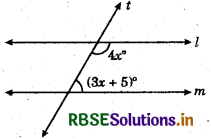
(a) x = 35
(b) x = 30
(c) x = 25
(d) x = 20
Answer:
(c) x = 25

II. Fill in the Blanks :

Question 1.
If the complementary angles are in the ratio 1: 5, then the measure of the angles are _________ and _________ respectively.
Answer:
15°, 75°

Question 2.
The sum of two adjacent angles is 100° and one of them is 35°, then the other is _________
Answer:
65°

Question 3.
If two interior angles on the same side of a transversal intersecting two parallel lines are in the ratio 2 : 3, then the greater of the two angles is _________.
Answer:
108°

Question 4.
Lines which are parallel to the same line are _________.
Answer:
parallel to each other

Question 5.
If two parallel lines are intersected by a transversal, then each pair of alternate angles are _________.
Answer:
equal.

III. True/False:
State whether the following statements are True or False.

Question 1.
Two congruent angles have same measure.
Answer:
True

Question 2.
If a transversal intersects two parallel lines, then each pair of interior angles on the same side of transversal is complementary.
Answer:
False

Question 3.
If the sum of two adjacent angles is 180°, then the non-common arms of the angles form a line.
Answer:
True

Question 4.
A ray has a finite length.
Answer:
False

Question 5.
Lines parallel to the same line are parallel to each other.
Answer:
True

Question 6.
If a line is perpendicular to one of the two given parallel lines then it is perpendicular to the other line.
Answer:
True

Question 7.
If two parallel lines are intersected by a transversal, then each pair of corresponding angles is equal.
Answer:
True

IV. Match the Columns :

Question 1.
Match the column I with the column II.

Column I	Column II
(1) If x° and y° be the measures of two complementary angles, such that 2x = 3y, then x =	(i) 45°
(2) If an angle is the supplement of itself, then the measure of the angle is	(ii) 60°
(3) If an angle is the complement of itself, then the measure of the angle is	(iii) 54°
(4) If x° andy° be the angles forming a linear pair, such that x - y = 60°, then	(iv) 90°

Answer:

Column I	Column II
(1) If x° and y° be the measures of two complementary angles, such that 2x = 3y, then x =	(iii) 54°
(2) If an angle is the supplement of itself, then the measure of the angle is	(iv) 90°
(3) If an angle is the complement of itself, then the measure of the angle is	(i) 45°
(4) If x° andy° be the angles forming a linear pair, such that x - y = 60°, then	(ii) 60°

V. Very Short Answer Type Questions :

Question 1.
Two lines l and m are perpendicular to the same line n. Are l and m perpendicular to each other? Give reason for your answer.
Answer:
No, since l and m are perpendicular to the line n‘.

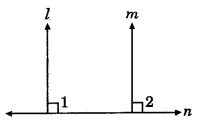
∠1 = ∠2 = 90° (∵ l ⊥ n and min)
It implies that these are corresponding angles.
Hence, l ∥ m.

Question 2.
If one angle is equal to four times of its complement. Find the angle.
Answer:
Let the angle be x.
Then, x = 4(90° - x)
x = 360° - 4x
⇒ 5x = 360°
⇒ x = \(\frac{360^{\circ}}{5}\) = 72°
⇒ 360° = 72°

Question 3.
Find the supplement of \(\frac{3}{5}\) of a right angle.
Answer:
Given angle \(\frac{3}{5}\) of a right angle = \(\frac{3}{5}\) × 90° = 3 × 18° = 54°
Supplement of 54° = An angle of measure (180° - 54°)
= An angle of measure 126°
Hence, the required angle is 126°.

Question 4.
In the figure below, l₁ ∥ l₂ and a₁ ∥ a₂. Find the value of x.

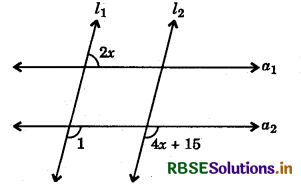
Answer:
∠1 = 4a + 15 (Corresponding angles)
2a = 180 - ∠1 (Corresponding angles)
⇒ 2a = 180° - (4a + 15)
⇒ 2a = 165 - 4x
⇒ 6a = 165 ⇒ x = \(\frac{165}{6}\) = 27\(\frac{1^{\circ}}{2}\)

Question 5.
Determine the value of x.

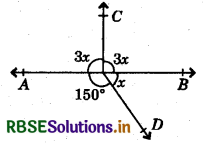
Answer:
Here,
3x + 3x + x + 150° = 360°
⇒ 7x + 150° = 360°
⇒ 7x = 360° - 150° = 210°
⇒ x = \(\frac{210^{\circ}}{7}\) = 30°

VI. Short Answer Type Questions:

Question 1.
In the given figure, if l ∥ n in, then find the value of x.
Answer:
Draw a line EF such that EF ∥ l ∥ m.

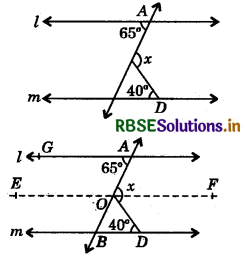
Then, ∠FOD = ∠BDO = 44°
(Alternate interior angles)
and ∠FOA = ∠CAO = 65°
(Alternate interior angles)
Now, ∠x = ∠FOD + ∠FOA
= 44° + 650 = 105°

Question 2.
In ΔABC, ∠A = \(\frac{\angle B}{2}=\frac{\angle C}{6}\) then find the measure of ∠A.
Answer:
As in a ΔABC,
Given that ∠A + ∠B + ∠C = 180° ...(i)
⇒ ∠B = 2∠A
∠A = (Given) ....(2)
⇒ ∠C = 6∠A ...(3)

Substituting eq. (2) and (3) in (1), we get: ∠A + 2∠A + 6∠A = 180°
9∠A = 180°
∠A = \(\frac{180^{\circ}}{9}\) = 20°
∠A = 20

Question 3.
Ray Obisects ∠AOB and OF is the ray opposite to 0E. Show that ∠FOB = ∠FOA.

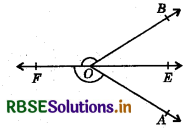
Answer:
∠FOB + ∠BOE = 180° ............(1) (Linear pair axiom)
∠FOA + ∠AOE = 180°
From equations (1) and (2),
∠FOB + ∠BOE = ∠FQA + ∠AOE
But, ∠BOE = ∠AOE (∵ Ray OE bisects ∠AOB)
∴ From equation (3),
⇒ ∠FOB = ∠FOA.
Hence proved.

Question 4.
In the given figure, AC ⊥ CE and ∠A: ∠B: ∠C = 5:3: 2. Find the value of ∠ECD.

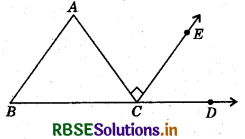
Answer:
Let ∠A = 5x, ∠B = 3x and ¿C =
In ΔABC, we have ∠A + ∠B + ∠C = 180°
⇒ 5x + 3x + 2x = 180°
⇒ x = \(\frac{180^{\circ}}{10}\) = 18°

∴ ∠A = 5x = 5 × 18° = 90°
∠B = 3x = 3 × 18° = 54° -
∠C = 2x = 2 × 18° = 36°
∠ACD = ∠BAC + ∠ABC
(∵ Exterior angle = Sinn of interior opposite angles)

⇒ ∠ACE + ∠ECD = 90° + 54°
∴ ∠ECD = 54° (∵ ∠ACE = 90°)

Question 5.
In the given figure, if AB ∥ CD, then find the value of x.

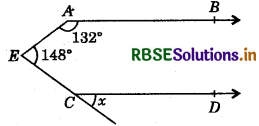
Answer:
Draw a line EF ∥ AB ∥ CD.

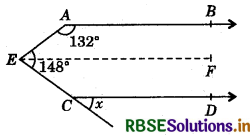
Since, AB ∥ EF and AE is a transversal.
∴ ∠BAE + ∠AEF = 180° (Co-interior angles)
⇒ 132° + ∠AEF = 180°
⇒ ∠AEF = 180° - 132° = 48°
Now, ∠FEC = ∠AEC - ∠AEF
= 148° - 48° = 100°

Since, EF ∥ CD and EC is a transversal.
∠FEC = ∠x - 100°
(By corresponding angles axiom)

Question 6.
In the given figure, what value of x will make RF ∥ CD, if AR ∥ CD?

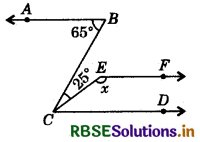
Answer:
Giyen, AB ∥ CD and BC is a transversal.
⇒ ∠ABC = ∠BCD (Alternate interior angles)
⇒ ∠ABC = ∠BCE + ∠ECD
⇒ 65° = 250 + ∠ECD 
∠ECD = 65° - 25°
⇒ ∠ECD = 40°
For EF CD, the sum of ∠FEC and ∠ECD should be equal to 180°.
∴ x + ∠ECD = 180° (Co-interior angles)
⇒ x + 40° = 180°
⇒ x = 180° - 40° = 140°
Hence, for x = 140°, EF will be parallel to CD.

Question 7.
In the given figure, QO and RO are the bisectors of Q and R, respectively. If ∠QPR = 75° and ∠PQR = 56°, then find the measure of ∠ORQ.

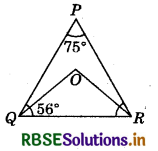
Answer:
In ΔPQR, we have ∠P + ∠Q + ∠R = 180°
(Since, sum of all the angles of a triangle is 180°.)
75° + 56° + ∠R = 180°
∠R = 180° - (75° + 56°) = 49°
But, ∠ORQ = \(\frac{1}{2}\)∠R (Since, OR is the bisector of ¿R.)
∠ORQ = \(\frac{1}{2}\)(49°) = 24\(\frac{1}{2}\)°

VII. Long Answer Type Questions :

Question 1.
If two parallel lines are intersected by a transversal, prove that the bisectors of two pairs of interior angles enclose a rectangle.
Answer:
Given AB ∥ CD and a transversal ‘f intersects them at E and F respectively.
EG, FG, EH and FH are bisectors of interior angles ∠AEF, ∠CFE, ∠BEF and ∠EFD respectively.

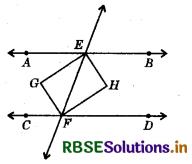
To prove : EGFH is a rectangle. -
Proof : AB ∥ CD and transversal‘t’ intersects them at E and F respectively.
⇒ ∠AEF = ∠EFD (Alternate interior angles)
⇒ \(\frac{1}{2}\)(∠AEF) = \(\frac{1}{2}\)(∠EFD)
∠GEF = ∠EFH

But, these are alternate interior angles formed when the transversal EF intersects EG and FH.
⇒ EG ∥ FH.
Similarly, EH ∥ GF. Therefore, EGFH is a ∥gm.
Now ray EF stands on line AB.
∠AEF + ∠BEF = 180° (Linear pair)
\(\frac{1}{2}\)(∠AEF) + \(\frac{1}{2}\)(∠BEF) = 90°
⇒∠GEF + ∠HEF = 90°
⇒ ∠GEH = 90°
Thus, EGFH parallelogram has one right angle.
∴ EGFH is a rectangle.
Hence proved.

Question 2.
In the given figure, if TU ∥ SR and TR ∥ SV, then find ∠a and ∠b.

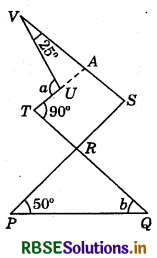
Answer:
Given, TU ∥ RS
∠UTR = ∠SRQ
(By corresponding angles axiom)
⇒ ∠SRQ = 90° (∵ ∠UTR = 90°)

In ΔRPQ, we have :
∠SRQ = ∠RPQ + ∠RQP
(∵ Exterior angle = Sum of interior opposite angles)
⇒ 90° = 50° + b
⇒ b = 90° - 50°
⇒ b = 40°
Also, given that TR ∥ SV
∠UTR = ∠VAU (Alternate interior angles)
∠VAU = 90° (∵ ∠UTR = 90°)
∠VUT = ∠UVA + ∠VAU
(∵ Exterior angle = Sum of interior opposite angles)
⇒ a = 25° + 90°
⇒ a = 115°
Hence, a = 115° and b = 40°.

Question 3.
The side BC of a ΔABC is produced, such that D is on ray BC. The bisector of A meet BC in L as shown in figure.

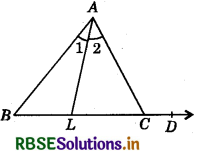
Prove that ∠ABC + ∠ACD = 2 ∠ALC.
Answer:
In ΔABC, we have : ext. ∠ACD = ∠B + ∠A
ext. ∠ACD = ∠B + 2∠A
(∵ AL is the bisector of ∠A)
∴ ∠A = 2∠1
⇒ ∠ACD = ∠B + 2∠1 ..........(1)

In ΔABL, we have :
ext. ∠ALC = ∠B + ∠BAL
⇒ ext. ∠ALC = ∠B + ∠1 ..........(2)
⇒ 2 .∠ALC = 2 ∠B + 2∠1 (Multiplying eq. (2) by 2)

Subtracting (1) from (2), we get:
2∠ALC - ∠ACD = 2∠B - ∠B + 2∠1 - 2∠1
2∠ALC - ∠ACD = ∠B
⇒ ∠ACD + ∠B = 2∠ALC
⇒ ∠ACD + ∠ABC = 2∠ALC.
Hence proved.