RBSE Class 9 Maths Important Questions Chapter 6 रेखाएँ और कोण

Rajasthan Board RBSE Class 9 Maths Important Questions Chapter 6 रेखाएँ और कोण Important Questions and Answers.

RBSE Class 9 Maths Chapter 6 Important Questions रेखाएँ और कोण

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
नीचे आकृति में वृहत् कोण, AOB बराबर है

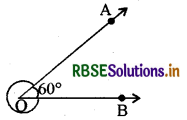
(A) 60°
(B) 120°
(C) 300°
(D) 360°
उत्तर:
(C) 300°

प्रश्न 2.
नीचे आकृति में दर्शाये गये कोण ∠AOB तथा ∠BOC हैं

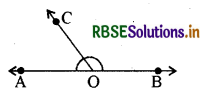
(A) पूरक कोण
(B) सम्पूरक कोण
(C) आसन्न कोण
(D) उपर्युक्त में से कोई नहीं
उत्तर:
(D) उपर्युक्त में से कोई नहीं

प्रश्न 3.
नीचे आकृति में दो सरल रेखाएँ AB तथा CD एक-दूसरे को 0 बिन्दु पर प्रतिच्छेद कर रही हैं और इस प्रकार बिन्दु 0 पर बने कोण अंकित हैं। यहाँ ∠x - ∠y का मान है

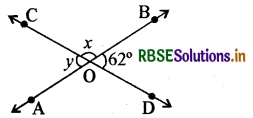
(A) 56°
(B) 118°
(C) 62°
(D) 180°
उत्तर:
(A) 56°

प्रश्न 4.
चित्र से बताइए कि निम्न में से कौन-सा कोण युग्म, संगत कोण नहीं है

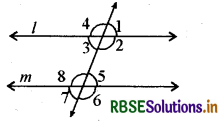
(A) ∠1, ∠5
(B) ∠2, ∠6
(C) ∠3, ∠7
(D) ∠3, ∠5
उत्तर:
(D) ∠3, ∠5

प्रश्न 5.
नीचे आकृति में दो समान्तर रेखाएँ । तथा m को एक तिर्यक रेखा n, बिन्दुओं G तथा H पर काट रही है, इस प्रकार बनने वाले कोण चित्र में अंकित हैं। यदि 11 न्यूनकोण हो, तो बताइए निम्न में से कौनसा कथन असत्य है

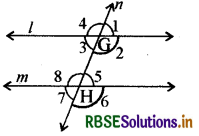
(A) ∠1 + ∠2 = 180°
(B) ∠2 + 15 = 180°
(C) ∠3 + ∠8 = 180°
(D) ∠2 + ∠6 = 180°
उत्तर:
(D) ∠2 + ∠6 = 180°

प्रश्न 6.
नीचे आकृति में दो समान्तर रेखाओं a तथा b को एक तिर्यक रेखा = बिन्दुओं A तथा B पर काटती है। A तथा B पर बनने वाले कोण आकृति में अंकित हैं। आकृति से बताइए कि निम्न में से कौनसे कोण युग्म का समान होना आवश्यक नहीं

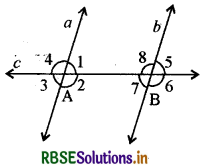
(A) ∠1, ∠2
(B) ∠1, ∠3
(C) ∠1, ∠5
(D) ∠2, ∠8
उत्तर:
(A) ∠1, ∠2

प्रश्न 7.
चित्र में रेखायें l तथा m समान्तर हैं, तो ∠x का मान क्या होगा?

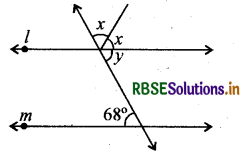
(A) 112°
(B) 56°
(C) 68°
(D) 28°
उत्तर:
(B) 56°

प्रश्न 8.
किसी बिन्दु पर बनने वाले समस्त कोणों का मान होता है
(A) चार समकोण
(B) दो समकोण
(C) तीन समकोण
(D) एक समकोण
उत्तर:
(A) चार समकोण

प्रश्न 9.
ऐसा कोण जिसका मान 180° है, कहलाता है
(A) न्यून कोण
(B) ऋजु कोण
(C) वृहत् कोण
(D) समकोण
उत्तर:
(B) ऋजु कोण

प्रश्न 10.
निम्न में से कौनसा चित्र आसन्न कोणों को प्रदर्शित नहीं करता

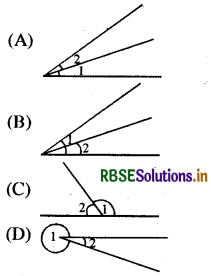
उत्तर:

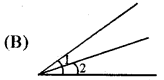
प्रश्न 11.
दिये गये चित्र में AB व CD समान्तर रेखाओं को तिर्यक EF बिन्दु G व H पर काटली है। ∠1 का संगत कोण है

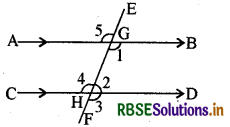
(A) ∠2
(B) ∠3
(C) ∠4
(D) ∠5
उत्तर:
(B) ∠3

प्रश्न 12.
दिये गये चित्र में AB ∥ CD हो, तो ∠1 + ∠2 का मान होगा

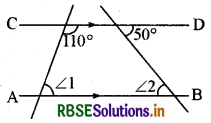
(A) 160°
(B) 80°
(C) 60° 
(D) 120°
उत्तर:
(D) 120°

प्रश्न 13.
दिए हए चित्र में AB ∥ CD तथा ∠BAE = x,∠AED = y और ∠EDC = 30° हो तो ∠x + ∠y का मान है

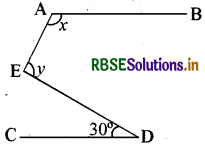
(A) 60°
(B) 120°
(C) 150°
(D) 210°
उत्तर:
(D) 210°

प्रश्न 14.
दिये गये चित्र में यदि AOB एक सरल रेखा है | तो कोण COD का मान होगा

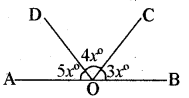
(A) 15°
(B) 45°
(C) 60°
(D) 75°
उत्तर:
(C) 60°

प्रश्न 15.
दो आसन्न कोण AOC तथा BOC इस प्रकार हैं कि∠AOC = 2∠BOC तथा ∠BOC = 60° तो AO और OB एक
(A) सरल रेखा में हैं।
(B) सरल रेखा में नहीं हैं।
(C) दूसरे के अभिलम्बवत् हैं।
(D) समान हैं।
उत्तर:
(A) सरल रेखा में हैं।

प्रश्न 16.
एक कोण अपने पूरक का तीन गुना है । तब कोण का माप है
(A) 130°
(B) 135°
(C) 90°
(D) 120°
उत्तर:
(B) 135°

प्रश्न 17.
यदि दो रेखाएँ AB तथा CD परस्पर O पर प्रतिच्छेदित होती हैं। यदि ∠BOD = 63°, तब ∠BOC =
(A) 63°
(B) 117°
(C) 17°
(D) 153°
उत्तर:
(B) 117°

प्रश्न 18.
यदि चित्र में, \(\frac{y}{x}\) = 5 और \(\frac{z}{x}\) = 4, तब x का मान है

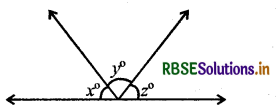
(A) 8°
(B) 18°
(D) 15°
(C) 12°
उत्तर:
(B) 18°

प्रश्न 19.
चित्र में, कौनसा कथन सत्य है?

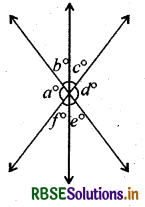
(i) a + b = d + c
(ii) a + c + e = 180°
(iii) b + f = c + e
(A) केवल (i)
(B) केवल (ii)
(C) केवल (iii)
(D) केवल (ii) एवं (iii)
उत्तर:
(D) केवल (ii) एवं (iii)

प्रश्न 20.
चित्र में AB ∥ CD ∥ EF तथा GH ∥ KL, तब ∠HKL है

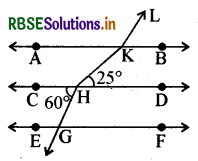
(A) 85°
(B) 135°
(C) 145°
(D) 215°
उत्तर:
(C) 145°

प्रश्न 21.
दो रेखाएँ AB व CD बिन्दु 0 पर प्रतिच्छेदित होती हैं। यदि ∠AOC + ∠COB + ∠BOD = 270°, तब ∠AOC =
(A) 70°
(B) 80°
(C) 90°
(D) 180°
उत्तर:
(C) 90°

प्रश्न 22.
चित्र में, यदि CP ∥ BQ, तब x का माप है

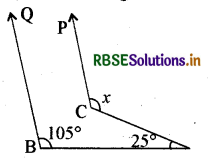
(A) 130°
(B) 105°
(C) 175°
(D) 125°
उत्तर:
(A) 130°

प्रश्न 23.
चित्र में, यदि रेखाएँ । एवं m समान्तर हैं, तब x = 

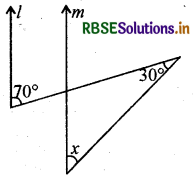
(A) 70°
(B) 100°
(C) 40°
(D) 30°
उत्तर:
(C) 40°

प्रश्न 24.
चित्र में, यदि l ∥ m, तब x =

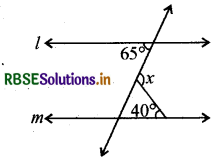
(A) 105°
(B) 65°
(C) 400
(D) 25°
उत्तर:
(A) 105°

प्रश्न 25.
यदि l ∥ m, (चित्र में), तब x =

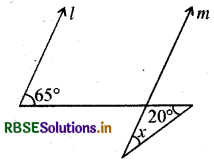
(A) 20°
(B) 45°
(D) 85°
(C) 65°
उत्तर:
(B) 45°

रिक्त स्थानों की पूर्ति करो

प्रश्न 1.
यदि एक कोण अपने पूरक का तीन गुना है तब कोण का माप __________ होगा।
उत्तर:
135°

प्रश्न 2.
ऐसा कोण जो दो समकोण से बड़ा एवं चार समकोण से छोटा हो, उसे __________ कहते हैं।
उत्तर:
वृहत् कोण

प्रश्न 3.
जब दो कोणों का योग 1 समकोण के बराबर हो - तो वे एक-दूसरे के __________ कहलाते हैं।
उत्तर:
पूरक कोण

प्रश्न 4.
यदि दो सरल रेखाएँ परस्पर प्रतिच्छेद करें तो इस प्रकार बने शीर्षाभिमुख कोण __________ होते
उत्तर:
बराबर

प्रश्न 5.
यदि दो या अधिक समान्तर रेखाओं को एक तिर्यक रेखा काटे तो संगत कोण __________ होते हैं।
उत्तर:
बराबर

प्रश्न 6.
यदि दो समान्तर रेखाओं को कोई एक तिर्यक - रेखा काटे तो एक ओर के अन्त:कोणों का योग __________ होता है।
उत्तर:
2 समकोण

प्रश्न 7.
एक ही रेखा पर खींचे गए लम्ब परस्पर __________ होते हैं।
उत्तर:
समान्तर

प्रश्न 8.
एक त्रिभुज के तीनों कोणों का योग __________ होता है।
उत्तर:
180°

सत्य/असत्य-निम्नलिखित कथनों के लिए सत्य अथवा असत्य लिखिए

प्रश्न 1.
जब दो कोणों का योग 2 समकोण के बराबर होता है, तो प्रत्येक कोण दूसरे कोण का सम्पूरक कोण कहलाता है।
उत्तर:
सत्य

प्रश्न 2.
ऐसा कोण जो दो समकोण के बराबर हो, अधिक कोण कहलाता है।
उत्तर:

प्रश्न 3.
यदि दो या अधिक समान्तर रेखाओं को एक तिर्यक रेखा काटे तो एकान्तर कोण सम्पूरक होते हैं।
उत्तर:
असत्य

प्रश्न 4.
यदि एक तिर्यक रेखा दो समान्तर रेखाओं को प्रतिच्छेदित करे तो संगत कोणों का प्रत्येक युग्म बराबर होता है।
उत्तर:
सत्य

प्रश्न 5.
किसी त्रिभुज में एक से अधिक अधिककोण नहीं हो सकते।
उत्तर:
सत्य

प्रश्न 6.
एक किरण की लम्बाई सीमित होती है।
उत्तर:
असत्य

प्रश्न 7.
यदि किसी त्रिभुज की एक भुजा को बढ़ाया जाए, तो इस प्रकार बना बहिष्कोण अपने दोनों अन्तःअभिमुख कोणों के योग से छोटा होता है।
उत्तर:
असत्य

प्रश्न 8.
शीर्षाभिमुख कोणों के अर्द्धक एक सरल रेखा में होते हैं।
उत्तर:
सत्य

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
नीचे दी गई आकृति में रेखाएँ l ∥ m एवं a ∥ b हों तो इसमें अंकित कोणों में समान कोण युग्मों को लिखिए।

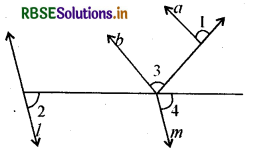
हल:
∠1 = ∠3 संगत कोण
तथा ∠2 = ∠4 संगत कोण

प्रश्न 2.
दिये गये चित्र में रेखाएँ EF ∥ GH हों तो ∠x का मान ज्ञात कीजिए।

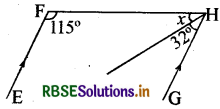
हल:
∠x + 32° + 115° = 180° (अन्तःकोण)
∠x = 180° - 147°
∠x = 33°

प्रश्न 3.
दी गई आकृति से बताइए कि क्या रेखाएँ l तथा m समान्तर हैं ? कारण भी स्पष्ट कीजिए।

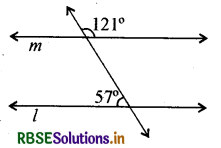
हल:
यहाँ 57° का एकान्तर कोण 180° - 121° के समान होना चाहिए किन्तु यहाँ 57° ≠ 59° है अतः l ∥ m नहीं है।

प्रश्न 4.
चित्र में रेखाएँ। तथा m समान्तर हैं तो ∠x का मान ज्ञात कीजिए। कारण भी स्पष्ट कीजिए।

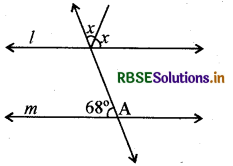
हल:
∴ ∠A = 180° - 68°
= 112°

∴ x + x = ∠A (संगत कोण)
2x = 112°
x = 56°
∴ ∠x = 56°

प्रश्न 5.
दी गई आकृति में AB ∥ CD एवं PQ ∥ EF हो तो ∠x का मान ज्ञात कीजिए।

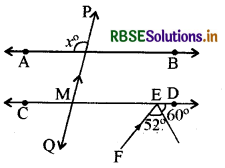
हल:
∠DEF = 60° + 52° = 112°
∠EMQ = ∠DEF (संगत कोण)
∠PMC = ∠EMQ = 112° (सम्मुख कोण)
∠x = ∠PMC = 112° (संगत कोण)

प्रश्न 6.
न्यून कोण किसे कहते हैं ?
उत्तर:
वह कोण जो समकोण से छोटा होता है, न्यून कोण कहलाता है।

प्रश्न 7.
वृहत् कोण की परिभाषा दीजिए।
उत्तर:
वह कोण जो दो समकोण से बड़ा तथा चार समकोण से छोटा हो, वृहत् कोण कहलाता है।

प्रश्न 8.
समकोण, अधिक कोण और न्यून कोण में अन्तर स्पष्ट करो।
उत्तर:
समकोण-90° के कोण को समकोण कहते हैं। न्यूनकोण-इसका मान समकोण से कम होता है। अधिक कोण-इसका मान समकोण से अधिक होता

प्रश्न 9.
एक ही बिन्दु पर बनने वाले समस्त कोणों का मान कितना होता है?
उत्तर:
4 समकोण के बराबर होता है।

प्रश्न 10.
दो पूरक कोण आपस में समान हैं तो प्रत्येक का मान लिखो।
उत्तर:
प्रत्येक कोण 45° का होगा।

प्रश्न 11.
90° के कोण के पूरक कोण का परिमाण लिखो।
उत्तर:
शून्य या 0°

प्रश्न 12.
सम्पूरक कोण किसे कहते हैं ?
उत्तर:
यदि दो कोणों का योग दो समकोण के तुल्य हो तो वे एक-दूसरे के सम्पूरक कोण कहलाते हैं।

प्रश्न 13.
पूरक कोण की परिभाषा दीजिए।
उत्तर:
यदि दो कोणों का योग एक समकोण के समान हो तो वे एक-दूसरे के पूरक कोण कहलाते हैं।

प्रश्न 14.
एक कोण अपने पूरक कोण का आधा है तो उस कोण का मान ज्ञात करो।
हल:
x + \(\frac{1}{2}\)x = 90°
या \(\frac{3}{2}\)x = 90°
3x = 180°
x = 60°
∴ तथा कोण का मान = \(\frac{60^{\circ}}{2}\)= 30°

प्रश्न 15.
नीचे चित्र में दो रेखाएँ एक-दूसरे को काटती हैं। यदि ∠1 + ∠3 = 70° है तो ∠2 का मान ज्ञात करो।

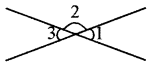
हल:
∠1 = ∠3 = \(\frac{70^{\circ}}{2}\) = 35°
अतः ∠2 = 180° - ∠3
= 180° - 35° = 145°

प्रश्न 16.
यदि AB, EF और CD तीन समान्तर रेखाएँ हों तथा ∠BAO = 35° और ∠AOC = 90° हों, तो ∠OCD का मान लिखिए।
हल:
∠AOC = 90°
अतः ∠AOE = 35° तथा

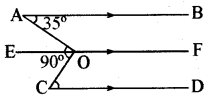
∠EOC = 90° - 35°
= 550
∠OCD = ∠EOC 
अतः ∠OCD = 55°

प्रश्न 17.
दी गई आकृति से ∠x का मान बताइए।

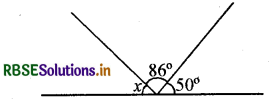
हल:
∠x = 180° - (86 + 50) (सरल रेखा युग्म कोण)
= 44°

प्रश्न 18.
संलग्न आकृति में संलग्न कोणों के कितने युग्म हैं?

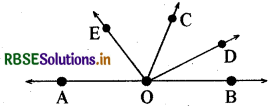
हल:
10 कोणों के युग्म हैं।

लघूत्तरात्मक प्रश्न

प्रश्न 1.
दिए हुए चित्र में l ∥ m कोण ∠1, ∠2, ∠3 और ∠4 का मान ज्ञात करो।

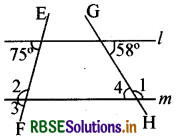
हल:
∠1 + 58° = 180°
∠1 = 180° - 58°
= 122°

तथा ∠2 + 75° = 180°
∠2 = 180° - 75°
= 105°
∠3 + ∠2 = 180°
∠3 = 180° - ∠2
∠3 = 180° - 105°
∠3 = 75°
∠4 = 58° एकान्तर कोण
अतः ∠1 = 122°, ∠2 = 105°, ∠3 = 75°, ∠4 = 58°

प्रश्न 2.
दिए हुए चित्र में x के किसी मान के लिए बिन्दु B, O और A एक ही सरल रेखा में हैं, तो ∠BOC और ∠AOC के मान ज्ञात करो।

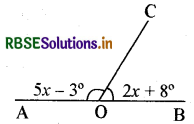
हल:
2x + 8 + 5x - 3 = 180° (आसन्न कोण)
या 7x + 5 = 180°
या 7x = 180° - 5° = 175°
∴ x = \(\frac{175^{\circ}}{7}\) = 250
BOC = 2x + 8°
= 2 × 25° + 8°
= 50° + 8° = 58°
∠AOC = 5x - 3°
= 5 × 25° - 30
= 125° - 3° = 122°

प्रश्न 3.
दिए गए चित्र में रेखाएँ AB ∥ CD, ∠r = 30° एवं ∠y = 60° हैं। वृहत् कोण ∠BPD ज्ञात कीजिए।

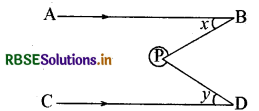
हल:
P में होकर PQ रेखा खींची जो AB व CD के समान्तर हो।

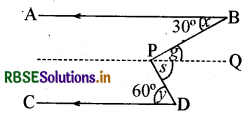
चित्र से
∠g = ∠x (एकान्तर कोण)
∠x = 309
∠g = 30°
∠s = ∠y (एकान्तर कोण)

संजीव पास बुक्स
और ∠y = 60°
∠s = 60°
अतः ∠BPD = ∠g + ∠s
= 30° + 60° = 90°

अतः वृहत् कोण
∠BPD = 360°
∠90° = 270°

प्रश्न 4.
चित्र में रेखाएँ AB ∥ CD हैं। चित्र में दिए गए कोणों से Z तथा ∠y ज्ञात कीजिए।

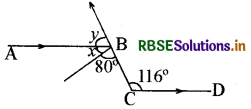
हल:
80° + 2x = 116° (एकान्तर कोण)
∠x = 116° - 80°
= 36°
∴ x + y + 80° = 180°
36° + y° + 80° = 180°
∠y = 180° - 80° - 36°
∠y = 64°

प्रश्न 5.
चित्र में रेखाओं l, m, n, p, q एवं में से कौन-कौनसी रेखाएँ समान्तर हैं और क्यों?

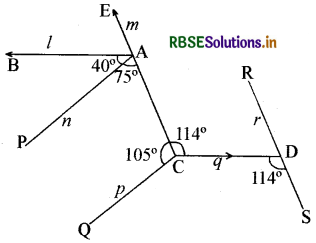
हल:
∠BAC = 40° + 75° = 115°
∠BAE = 180° - 115° = 65°
∠PAE = 40° + 65° = 105°
∠AE = ∠QCA = 105° (संगत कोण)
अतः n ∥ P
पुनः ∠CDS = ∠ACD = 114° (एकान्तर कोण)
∴ m व r समान्तर होगी m ∥ r उत्तर

प्रश्न 6.
नीचे दी गई आकृति में कौन-कौनसी रेखाएँ । समान्तर हैं और क्यों?

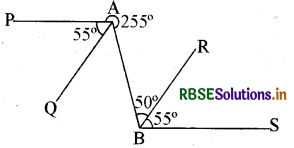
हल:
∠QAB = 360° - (55° + 255°)
= 50°
तथा ∠ABR = 50° 
∠QAB = ∠ABR
अत: AQ ∥ BR (एकान्तर कोण समान होने के कारण) उत्तर
पुनः ∠PAB = 55° + 50° = 105° तथा
∠ABS = 50° + 55° = 105°
अतः PAB = ∠ABS (एकान्तर कोण)
अतः PA ∥ BS उत्तर

प्रश्न 7.
नीचे दी गई आकृति में AC ∥ PQ एवं AB ∥ RS तो ∠y का मान ज्ञात कीजिए। प्रयोग में आने वाले कथन के कारण भी लिखिए।

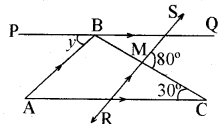
हल:
ΔRCM में बहिष्कोण
80° = ∠R + 30°
अतः - R = 80° - 30° = 50°
∠A = ∠R संगत कोण
तथा ∠y = ∠A एकान्तर कोण
अतः ∠y = 50°

प्रश्न 8.
आकृति में, AB ∥ CD और CD ∥ EF है। साथ ही, EA ⊥ AB है। यदि ∠BEF = 55° है, तो x,y और z के मान ज्ञात कीजिए।

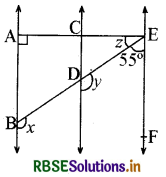
हल:
y + 55° = 180° (CD ∥ EF, तिर्यक रेखा ED के एक ही ओर के अंत:कोण)
अतः ∴ y = 180° - 55° = 125° 
पुनः ∴ x = y (AB ∥ CD, संगत कोण अभिगृहीत)
इसलिए x = 125°
अब चूँकि AB ∥ CD और CD ∥ EF है,
इसलिए AB ∥ EF है।
अत: ∠EAB + ∠FEA = 180° (तिर्यक रेखा EA के एक ही ओर के अंत:कोण)
इसलिए 90° + z + 55° = 180°
जिससे z = 35° प्राप्त होता है।

प्रश्न 9.
आकृति में, यदि QT ⊥ PR, ∠TQR = 40° और ∠SPR = 30° है, तो और y ज्ञात कीजिए।

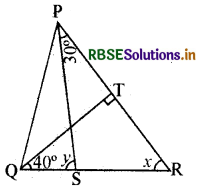
हल:
ΔTQR में, 90° + 40° + x = 180° (त्रिभुज का कोण योग गुण)
अतः x = 50° 
अब y = ∠SPR + x 
किसी त्रिभुज का बहिष्कोण अपने दोनों अंतः अभिमुख कोणों के योग के बराबर होता है।
अतः y = 30° + 50° = 80°

प्रश्न 10.
AB, CD और EF, O में से गुजरती तीन संगामी रेखाएँ इस प्रकार हैं कि OF, ∠BOD को समद्विभाजित करती हैं। यदि ∠BOF = 35° हो, तो ∠BOC और ∠AOD ज्ञात कीजिए।
हल:
प्रश्नानुसार क्योंकि OF रेखा ∠BOD को समद्विभाजित करती है।
∠BOF = ∠DOF = 35°
∠BOD = 70°
अब ∠BOD + ∠BOC = 180° (रैखिक युग्म अभिगृहीत)
या 70° + ∠BOC = 180°
∠BOC = 180° - 70°
∠BOC = 110°

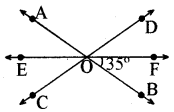
या ∠BOC = ∠AOD = 110° (∵ ये शीर्षाभिमुख कोण हैं)
अत: अभीष्ट ∠BOC = 110° और ∠AOD = 110°

प्रश्न 11.
नीचे दी गई आकृति में यदि x = y तथा a = b हो, तो सिद्ध कीजिए कि r ∥ n

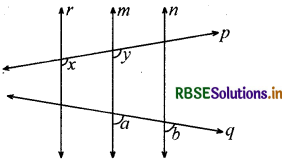
हल:
प्रश्नानुसार क्योंकि a = b (दिया है)
ये संगत कोण हैं। जब संगत कोण बराबर हों, तो रेखाएँ समान्तर होती हैं।
m ∥  n .....(i)
इसी प्रकार x = y (संगत कोण)
अतः r ∥ m ...........(ii)

समीकरण (i) व (ii) से
m ∥ n ∥ r या यह भी कहा जा सकता है कि r ∥ n (इति सिद्धम्)

प्रश्न 12.
दी गई आकृति में रेखाएँ PQ तथा RS परस्पर बिन्दु 0 पर प्रतिच्छेद करती हैं। यदि ∠POR: ∠ROQ = 5:7 है, तो सभी कोण ज्ञात कीजिए।

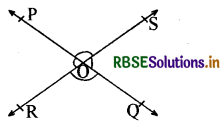
हल:
चित्रानुसार, ∠POR + ∠ROQ = 180° (रैखिक युग्म के कोण)
परन्तु ∠POR : ∠ROQ = 5 : 7 (दिया है)
अतः POR = \(\frac{5}{12}\) × 180° = 75°

संजीव पास बुक्स
इसी प्रकार 2 ROQ = \(\frac{7}{12}\) × 180° = 105°
अब ∠POS = ∠ROQ = 105° (शीर्षाभिमुख कोण)
और ∠SOQ = ∠POR = 75° (शीर्षाभिमुख कोण)

प्रश्न 13.
नीचे दिए गए त्रिभुज का एक बहिष्कोण 115° है और अंतः अभिमुख कोण 35° का है। शेष दोनों कोणों का मान ज्ञात कीजिए।

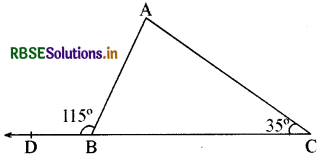
हल:
प्रश्न में दी गई आकृति के अनुसार
∠ABD + ∠ABC = 180° (रैखिक युग्म अभिगृहीत से)
या 115° + ∠ABC = 180°
∠ABC = 180° - 115°
या ∠ABC = 65°
अब ΔABC में
∠A + ∠ABC + ∠C = 180°
[क्योंकि त्रिभुजं के तीनों कोणों का योगफल 180° होता है।]
∴ ∠A+ 65° + 35° = 180° या
∠A = 180° - 65° - 35°
या ∠A = 80°
अतः शेष दोनों कोण क्रमश: 65° व 80° के हैं।

प्रश्न 14.
नीचे दी गई आकृति में ΔABC की भुजा BC को R तक बढ़ाया गया है। यदि ∠A : ∠B : ∠C = 3 : 2 : 1 हो और CS ⊥ AC हो, तो ∠SCR का मान ज्ञात कीजिए।

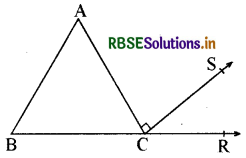
हल:
प्रश्नानुसार यह दिया गया है कि ΔABC में
∠A : ∠B : ∠C = 3 : 2 : 1 यदि x एक समानुपातिक स्थिरांक है तो
3x + 2x + x = 180° [क्योंकि त्रिभुज के तीनों कोणों का योगफल 180° होता है।]
6x = 180°
⇒ x = 30°
∠A = 3x = 3 × 30 = 90°
∠B = 2x = 2 × 30 = 60°
∠R = x = 1 × 30° = 30°
अब ΔABC में
∠ACR = ∠A + ∠B [क्योंकि ये ΔABC का बहिष्कोण है।]
या ∠ACR = 90° + 60°
∠ACS + ∠SCR = 90° + 60°
या 90° + ∠SCR = 90° + 60°
अत: ∠SCR = 60°

प्रश्न 15.
चित्र में ∠1 तथा ∠2 रैखिक कोण युग्म हैं, यदि ∠2 - ∠1 = 18° हो, तो ∠1 तथा ∠2 ज्ञात कीजिए।

हल:
दिया है
∠2 - ∠1 = 18° ........(i)
तथा ∠2 + ∠1 = 180° ....(ii)
समीकरण (i) और (ii) को जोड़ने पर,
2 × ∠2 = 198
या ∠2 = \(\frac{198}{2}\) = 99°
∠2 का मान समीकरण (ii) में रखने पर,
∠1 = 180° - 99° = 81°
अतः ∠1 = 81°
तथा ∠2 = 99°

प्रश्न 16.
दी गई आकृति में यदि ∠1 + ∠3 = 120° हो तो ∠3 एवं ∠4 के मान ज्ञात कीजिए।

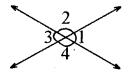
हल:
यहाँ ∠1 + ∠3 = 120°
किन्तु ∠1 = ∠3
अतः 2∠3 = 120°
या ∠3 = \(\frac{120^{\circ}}{2}\) = 60°
∠4 = 180° - ∠3
= 180° - 60° = 120°

प्रश्न 17.
दी गई आकति से ∠AOB, ∠COD एवं ∠EOF ज्ञात कीजिए।

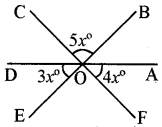
हल:
DA एक सरल रेखा है। अतः ∠DOC = ∠AOF = 4x°
∠BOA = ∠DOE = 3x°
अत: DA रेखा के समस्त कोणों का योग ∠DOC + ∠COB + ∠AOB = 180°
या 4x° + 5x° + 3x° = 180° या
12x° = 180°
x = \(\frac{180^{\circ}}{12}\) = 150
अतः ∠AOB = 3x° = 3 × 15° = 45°
∠COD = 4x° = 4 × 15° = 60°
∠EOF = 5x° = 5 × 15° = 75°

निबन्धात्मक प्रश्न

प्रश्न 1.
साथ के चित्र में यदि FG ∥ HK तो निम्न प्रश्नों के उत्तर कारण सहित दो-

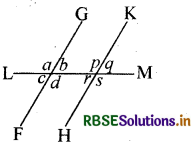
(i) यदि ∠b = / 70°, तो ∠r का मान ज्ञात करो।
(ii) यदि ∠s = 105°, तो ∠d का मान ज्ञात करो।
(iii) यदि ∠c = 65°, तो ∠p का मान ज्ञात करो।
(iv) यदि ∠q = 80°, तो ∠d का मान ज्ञात करो।
(v) यदि ∠a = 2q, तो ∠q का मान ज्ञात करो।
(vi) यदि ∠d = ∠r = 72°, तो ∠r का मान ज्ञात करो।
हल:
(i) ∠b = ∠r = 70° .....(एकान्तर कोण)

(ii) ∠d = ∠s ......(संगत कोण)
∴ ∠d = ∠s = 105°

(iii) ∠c = ∠b.....(शीर्षाभिमुख कोण)
∠b+ ∠p = 180° .....(अन्तःकोण)
∴ ∠c + ∠p = 180°
∴ ∠p = ∠180° - ∠c = 180° - 65° = 115°

(iv) ∠q = ∠r = 80° .....(शीर्षाभिमुख कोण) पर ∠r + ∠d = 180° .....(एक ही ओर के अन्तर कोण)
∠d = 180° - ∠r
= 180° - 80° = 100°
∠a = 2∠q .....(दिया हुआ है)
∠a = ∠p .....(संगत कोण)
∠p = 2∠q किन्तु
∠p + ∠q = 180° .....(संलग्न संपूरक कोण)
∴ 2∠q + ∠q = 180°
∴ 3 ∠q = 180°
∴ ∠q = 60°

(vi) ∠d - ∠r = 72°.....(दिया हुआ है)
∠d + ∠r = 180° .....(अन्तःकोण) घटाने पर,
2∠r = 180° - 72° = 108°
∴ ∠r = 540 

प्रश्न 2.
आकृति में, OP, OQ, OR और OS चार किरणें हैं। सिद्ध कीजिए कि ∠POQ + ∠QOR + ∠SOR + ∠POS = 360° है।

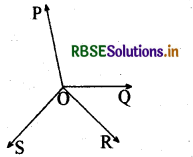
हल:
आकृति में, आपको किरणों OP, OQ, OR और OS में से किसी एक को पीछे एक बिन्दु तक बढ़ाए जाने की आवश्यकता है। आइए किरण OQ को एक बिन्दु.T तक पीछे बढ़ा दें ताकि TOQ एक रेखा हो (देखिए आकृति)।

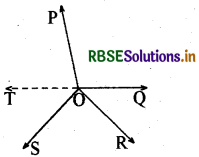
अब किरण OP रेखा TOQ पर खड़ी है। अत: ∠TOP + ∠POQ = 180° .....(1)
(रैखिक युग्म अभिगृहीत) इसी प्रकार, किरण OS रेखा TOQ पर खड़ी है।
अतः ∠TOS + ∠SOQ = 180° .....(2)
परन्तु ∠SOQ = ∠SOR + ∠OOR है।
अतः (2) निम्न हो जाती है ∠TOS + ∠SOR + ∠QOR = 180° .....(3)

अब (1) और (3) को जोड़ने पर, आपको प्राप्त होगा
∠TOP + ∠POQ + ∠TOS + ∠SOR + ∠QOR = 360°

परन्तु ∠TOP + ∠TOS = ∠POS है। 
अतः (4) निम्न हो जाती है-
∠POQ + ∠QOR + ∠SOR + ∠POS = 360°

प्रश्न 3.
यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार प्रतिच्छेद करे कि संगत कोणों के एक युग्म के समद्विभाजक परस्पर समान्तर हों, तो सिद्ध कीजिए कि दोनों रेखाएँ भी परस्पर समान्तर होती हैं।
हल:
आकृति में, एक तिर्यक रेखा AD दो रेखाओं PO और RS को क्रमशः बिन्दुओं B और C पर प्रतिच्छेद करती है। किरण BE, ∠ABQ की समद्विभाजक है और किरण CG ∠BCS की समद्विभाजक है तथा BE ∥ CG है।

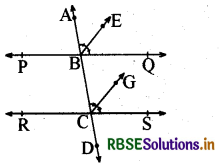
हमें सिद्ध करना है कि PQ ∥ RS है।

यह दिया है कि किरण BE, ∠ABQ की समद्विभाजक है।
अतः ∠ABE = \(\frac{1}{2}\)∠ABQ ...(1)
इसी प्रकार किरण CG, ∠BCS की समद्विभाजक
अतः CBCG = \(\frac{1}{2}\)∠BCS .....(2)

परन्तु BE ∥ CG है और AD एक तिर्यक रेखा है।
अतः ∠ABE = ∠BCG .....(3)
.(संगत कोण अभिगृहीत)

(3) में, (1) और (2) को प्रतिस्थापित करने पर, आपको प्राप्त होगा
∠ABQ = \(\frac{1}{2}\)∠BCS
अर्थात् ∠ABQ = ∠BCS
परन्तु, ये तिर्यक रेखा AD द्वारा रेखाओं PO और RS के साथ बनाए गए संगत कोण हैं और ये बराबर हैं।
अतः PQ ∥ RS (संगत कोण अभिग्रहीत का विलोम)

प्रश्न 4.
आकृति में, ΔABC की भुजाओं AB और AC को क्रमश: E और D तक बढ़ाया गया है। यदि ∠CBE और ∠BCD के समद्विभाजक क्रमश: BO और CO बिन्दु पर मिलते हैं, तो सिद्ध कीजिए कि ∠BOC = 90° - \(\frac{1}{2}\)∠BAC है।

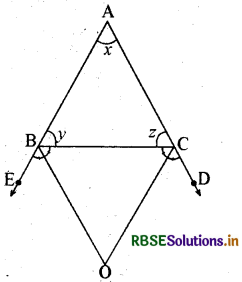
हल:
किरण BO कोण CBE की समद्विभाजक
अतः
∠CBO = \(\frac{1}{2}\)∠CBE
= \(\frac{1}{2}\)(180° –y)
= 90° - \(\frac{1}{2}\) ...(1)

इसी प्रकार, किरण CO कोण BCD की समद्विभाजक है।
अतः ∠BCO = \(\frac{1}{2}\)∠BCD
=  (180° - z)
= 90° - \(\frac{z}{2}\) ...(2)
ΔBOC में, ∠BOC + ∠BCO + ∠CBO = 180° है। .....(3)

(1) और (2) को (3) में रखने पर,
∠BOC + 90° - \(\frac{z}{2}\) + 90° - \(\frac{y}{2}\) = 180°
इसलिए ∠BOC = \(\frac{z}{2}+\frac{y}{2}\)
या ∠BOC = \(\frac{1}{2}\)(y + z) ....(4)
परन्तु x + y + z = 180° (त्रिभुज का कोण योग गुण) 
अतः y + x = 180° - x

इससे (4) निम्न हो जाता है-
∠BOC = 7 (180° - x)
= 90° - \(\frac{x}{2}\)
= 90° - \(\frac{1}{2}\) ∠BAC (इति सिद्धम्)

प्रश्न 5.
नीचे दी गई आकृति में किरण os रेखा POQ पर खड़ी है। किरण OR और OT क्रमशः ∠EOS और ∠SOQ के समद्विभाजक हैं। यदि ∠POS = x है, तो ∠ROT ज्ञात कीजिए।

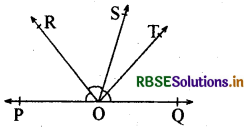
हल:
प्रश्नानुसार किरण OS रेखा POQ पर खड़ी है।
अतः ∠POS + ∠SOQ = 180° परन्तु
∠POS = x
अतः x + ∠SOQ = 180°
∠SOQ = 180° - x
अब किरण OR, ∠POS को समद्विभाजित करती है।

इसलिए ∠ROS = \(\frac{1}{2}\) × ∠POS
= \(\frac{1}{2}\) × x = \(\frac{x}{2}\)

इसी प्रकार, ∠SOT = \(\frac{1}{2}\) × ∠SOQ
= \(\frac{1}{2}\) × (180° - x)
= 90° - \(\frac{x}{2}\)

अब ∠ROT = ∠ROS + ∠SOT
= \(\frac{x}{2}\) + 90° - \(\frac{x}{2}\)
= 90°

प्रश्न 6.
सिद्ध करो कि त्रिभुज के तीनों कोणों का योगफल दो समकोण के बराबर होता है।
हल:
दिया है-एक त्रिभुज ABC में उसके कोणों को ∠1, ∠2 तथा ∠3 द्वारा अंकित किया गया है।

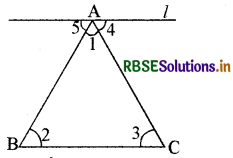
सिद्ध करना है - ∠1 + ∠2 + ∠3 = 180°
रचना - त्रिभुज ABC के शीर्ष बिन्दु A से गुजरती हुई एक सरल रेखा l, रेखा BC के समान्तर खींची।

उपपत्ति:
∵ BC ∥ l है अतः
∠2 = ∠5 (एकान्तर कोण).....(i)
एवं ∠3 = ∠4 (एकान्तर कोण).....(ii) 

समीकरण (i) और (ii) को जोड़ने पर
= ∠2 + ∠3 = ∠4 + ∠5 .....(iii)

(iii) के दोनों पक्षों में ∠1 जोड़ने पर
⇒ ∠1 + ∠2 + ∠3 = ∠1 + ∠4 + ∠5 .....(iv)

∵ रैखिक कोण युग्म अभिगृहीत से
∠1 + ∠4 + ∠5 = 180° .....(v)

(iv) व (v) से
∠1 + ∠2 + ∠3 = 180° (इति सिद्धम्)

प्रश्न 7.
सिद्ध करो कि यदि किसी त्रिभुज की एक भुजा बढ़ा दी जाए, तो इस प्रकार बना बहिष्कोण, अन्तःकोणों के योग के बराबर होता है।
हल:
दिया गया है-PQR एक त्रिभुज। सिद्ध करना है-
∠1 + ∠3 = ∠4 + ∠5
रचना - PQ के समान्तर RA खींची और QR को B तक बढ़ाया।
उपपत्ति - चूँकि PQ ∥ RA तथा QB इन्हें काटती है।

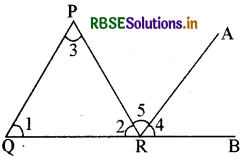
∠1 = ∠4 (संगत कोण).....(1)
इसी प्रकार PQ ∥ RA तथा PR इन्हें काटती है।
∠3 = ∠5 (एकान्तर कोण).....(2)

समीकरण (1) व (2) को जोड़ने पर
∠1 + ∠3 = ∠4 + ∠5
अतः यह कहा जा सकता है कि यदि किसी त्रिभुज की एक भुजा बढ़ा दी जाए, तो इस प्रकार बना बहिष्कोण अन्तराभिमुख अन्त:कोणों के योग के बराबर होता है। (इति सिद्धम्)

प्रश्न 8.
नीचे दी गई आकृति में यदि PQ ∥ RS, ∠MXQ = 135° और ∠MYR = 40° है, तो ∠XMY ज्ञात कीजिए।

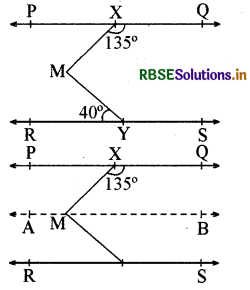
हल:
प्रश्न में दी गई आकृति में हमें m से होकर रेखा PQ के समान्तर एक रेखा AB खींचने की आवश्यकता है। (दूसरी आकृति के अनुसार)
अब AB ∥ PQ तथा PQ ∥ RS है। अतः AB ∥ RS होगी।
अब ∠QXM + ∠XMB = 180°
(AB ∥ PQ, तिर्यक रेखा XM के एक ही ओर के अंत:कोण हैं।)
परन्तु ∠QXM = 135° है।
∴ 135° + ZXMB = 180°

अतः ∠XMB = 45° .....(i)
अब ∠BMY = ∠MYR
(∵ AB ∥ RS एकान्तर कोण)
अतः ∠BMY = 40° .....(ii)

समीकरण (i) व (ii) को जोड़ने पर।
∠XMB + ∠BMY = 45° + 40°
अर्थात् ∠XMY = 85°

प्रश्न 9.
सिद्ध करो कि यदि दो समान्तर रेखाओं को एक तिर्यक रेखा काटे तो एक ओर के अन्तःकोणों का योग दो समकोण होता है।
हल:
दिया है-AB तथा CD दो समान्तर रेखाएँ हैं जिन्हें EF तिर्यक रेखा क्रमश: G तथा H बिन्दुओं पर काटती है। बिन्दुओं G तथा । पर क्रमशः कोण 21, 22, 23, 24 तथा 25, 26, 27, 28 बन रहे हैं। अन्त:कोण युग्म 22, 15 एवं 23, 18 हैं।

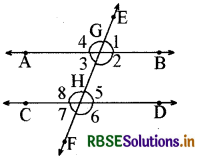
सिद्ध करना है ∠2 + ∠5 = 180°
एवं ∠3 + ∠8 = 180°
उपपत्तियहाँ ∠1 + ∠2 = 180° .....(i) (रैखिक कोण युग्म)
एवं ∠1 = ∠5 (संगत कोण)....(ii)

समीकरण (i) एवं (ii) से
∠2 + ∠5 = 180°
इसी प्रकार ∠3 + ∠4 = 180°.....(iii) (रैखिक कोण युग्म)
∠4 = ∠8 (संगत कोण)....(iv)

अतः समीकरण (iii) एवं (iv) से
∠3 + ∠8 = 180° (इति सिद्धम्)

प्रश्न 10.
सिद्ध करो कि यदि दो सरल रेखाओं को एक तिर्यक रेखा काटे और तिर्यक रेखा के एक ही ओर बने अन्तःकोणों का योग दो समकोण हो तो वे रेखाएँ समान्तर होंगी।
हल:
दिया है-AB तथा CD दो रेखाएँ हैं, इन्हें EF तिर्यक रेखा क्रमश: G एवं H बिन्दुओं पर काटती है। इस प्रकार बिन्दु G एवं H पर क्रमशः ∠1, ∠2, ∠3, ∠4 एवं ∠5, ∠6, ∠7, ∠8 बन रहे हैं।

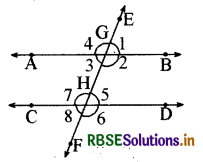
अन्त:कोण ∠2 + ∠5 = 180°
तथा ∠3 + ∠7 = 180°
सिद्ध करना है- AB ∥ CD

उपपत्तियहाँ ∠1 + ∠2 = 180° .....(i) (रैखिक कोण युग्म)
एवं ∠2 + ∠5 = 180° .....(ii) (दिया है)

समीकरण (i) एवं (ii) से
∠1 = ∠5 अतः संगत कोण अभिगृहीत से AB ∥ CD (इति सिद्धम्)