RBSE Class 9 Maths Important Questions Chapter 5 युक्लिड के ज्यामिति का परिचय

Rajasthan Board RBSE Class 9 Maths Important Questions Chapter 5 युक्लिड के ज्यामिति का परिचय Important Questions and Answers.

RBSE Class 9 Maths Chapter 5 Important Questions युक्लिड के ज्यामिति का परिचय

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
'ज्यामिति' यूनानी भाषा के किस शब्दों से मिलकर बना है?
(A) ज्यामिति से
(B) केवल ज्या से
(C) केवल मीटर्स से
(D) जियो और मेट्रन से
उत्तर:
(D) जियो और मेट्रन से

प्रश्न 2.
एक बारीक नोक वाली पेन्सिल से पैमाने के सहारे-सहारे नोक चलाने पर बनने वाली आकृति को कहते हैं
(A) रेखा
(B) रेखाखण्ड
(C) किरण
(D) बिन्दु
उत्तर:
(B) रेखाखण्ड

प्रश्न 3.
वह रेखाखण्ड जो वृत्त के केन्द्र से गुजरता है और जिसके दोनों सिरे वृत्त पर स्थित हों, कहलाता
(A) त्रिज्या
(B) व्यास
(C) त्रिज्याखण्ड
(D) वृत्तखण्ड
उत्तर:
(B) व्यास

प्रश्न 4.
वृत्त के प्रत्येक हिस्से को कहते हैं
(A) चाप
(B) व्यास
(C) त्रिज्याखण्ड
(D) वृत्तखण्ड
उत्तर:
(C) त्रिज्याखण्ड

प्रश्न 5.
"एक बिन्दु से एक अन्य बिन्दु तक एक सीधी रेखा खींची जा सकती है।" यह यूक्लिड की
(A) पहली अभिधारणा
(B) द्वितीय अभिधारणा
(C) तीसरी अभिधारणा
(D) चौथी अभिधारणा
उत्तर:
(A) पहली अभिधारणा

प्रश्न 6.
किसी रेखाखण्ड की लम्बाई होती है
(A) निश्चित दूरी
(B) अनिश्चित दूरी
(C) किन्हीं दो बिन्दुओं के बीच की दूरी
(D) अनन्त
उत्तर:
(C) किन्हीं दो बिन्दुओं के बीच की दूरी

प्रश्न 7.
दो बिन्दुओं से गुजरने वाली रेखाओं की संख्या कितनी होती है?
(A) एक
(B) दो
(C) तीन
(D) अनन्त
उत्तर:
(A) एक

प्रश्न 8.
यदि एक रेखा दो समान्तर रेखाओं पर गिरकर अपने एक ही ओर दो अन्तःकोणों का योग होगा
(A) 2 समकोण
(B) 180° से कम
(C) 180° से अधिक
(D) 360°
उत्तर:
(A) 2 समकोण

प्रश्न 9.
एक अद्वितीय रेखा कम से कम कितने बिन्दुओं से होकर जाती है
(A) एक
(B) दो
(C) तीन
(D) चार
उत्तर:
(B) दो

प्रश्न 10.
एक दिए गए बिन्दु से कितनी रेखाएँ गुजर सकती
(A) एक
(B) दो
(C) तीन
(D) अनन्त
उत्तर:
(D) अनन्त

प्रश्न 11.
दो भिन्न रेखाएँ अधिकतम कितने बिन्दुओं पर प्रतिच्छेद कर सकती हैं ?
(A) एक
(B) दो
(C) तीन
(D) अनगिनत
उत्तर:
(A) एक

प्रश्न 12.
यूक्लिड अभिगृहीत के अनुसार, वे वस्तुएँ जो एक-दूसरे के सम्पाती हों, एक-दूसरे के होती
(A) अलग-अलग
(B) बराबर
(C) शेष
(D) पूरक
उत्तर:
(B) बराबर

प्रश्न 13.
यूक्लिड की अभिधारणाओं के अनुसार, सभी समकोण एक-दूसरे के होते हैं
(A) पूरक
(B) सम्पूरक
(C) बराबर
(D) भिन्न
उत्तर:
(C) बराबर

प्रश्न 14.
किसी पृष्ठ के किनारे होते हैं
(A) बिन्दु
(B) रेखाएँ
(C) चाप
(D) कोण
उत्तर:
(B) रेखाएँ

प्रश्न 15.
एक रेखा के सिरे होते हैं
(A) बिन्दु
(B) रेखाएँ
(C) चाप
(D) कोण
उत्तर:
(A) बिन्दु

रिक्त स्थानों की पूर्ति करो

प्रश्न 1.
पिरामिड का आधार सदैव एक ______________ होता है।
उत्तर:
बहुभुज

प्रश्न 2.
एक अद्वितीय रेखा कम से कम ______________ बिन्दुओं से होकर जाती है।
उत्तर:
दो

प्रश्न 3.
एक दिए गए बिन्दु से ______________ रेखाएँ गुजरती हैं।
उत्तर:
अनन्त

प्रश्न 4.
दो भिन्न रेखाएँ अधिकतम ______________ बिन्दु पर प्रतिच्छेद करती हैं।
उत्तर:
एक

प्रश्न 5.
दो समतलों का प्रतिच्छेदन सदैव एक ______________ होती है।
उत्तर:
सरल रेखा

प्रश्न 6.
यूक्लिड अभिगृहीत के अनुसार, वे वस्तुएँ जो एक दूसरे के सम्पाती हों, एक-दूसरे के ______________ होती हैं।
उत्तर:
बराबर

प्रश्न 7.
यूक्लिड की अभिधारणाओं के अनुसार, सभी समकोण एक-दूसरे के ______________ होते हैं।
उत्तर:
बराबर

सत्य/असत्य-निम्नलिखित कथनों के लिए सत्य अथवा असत्य लिखिए

प्रश्न 1.
यूक्लिड के एक अभिगृहीत के अनुसार, यदि बराबरों को बराबरों में जोड़ा या घटाया जाये, तो पूर्ण भी बराबर होते हैं।
उत्तर:
सत्य

प्रश्न 2.
यूक्लिड के एक अभिगृहीत के अनुसार पूर्ण अपने भाग से छोटा होता है।
उत्तर:
असत्य

प्रश्न 3.
यूक्लिड की एक अभिधारणा के अनुसार एक बिन्दु से एक अन्य बिन्दु तक एक सीधी रेखा खींची जा सकती है।
उत्तर:
सत्य

प्रश्न 4.
यूक्लिड की पाँचवीं अभिधारणा के अनुसार, दो भिन्न प्रतिच्छेदी रेखाएँ एक ही रेखा के समान्तर हो सकती हैं।
उत्तर:
असत्य

प्रश्न 5.
एक सांत रेखा दोनों ओर अनिश्चित रूप से बढ़ाई नहीं जा सकती है।
उत्तर:
असत्य

प्रश्न 6.
ऐसे दो कोण जिनका शीर्ष एवं एक भुजा उभयनिष्ठ हो, आसन्न कोण कहलाते हैं।
उत्तर:
सत्य

प्रश्न 7.
ज्यामिति में ऐसी अनेक रचनाएँ होती हैं, जिन्हें बिना प्रमाण के सत्य माना जाता है तथा इनके आधार पर अन्य ज्यामितीय रचनाओं या तथ्यों को सिद्ध किया जाता है; अभिगृहीत कहलाते हैं।
उत्तर:
सत्य

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
ज्यामिति किसे कहते हैं ?
उत्तर:
गणित की जिस शाखा के अन्तर्गत बिन्दुओं, रेखाओं, तलों और ठोस पिण्डों के आकार, विस्तार और गुणों का अध्ययन किया जाता है, उसे ज्यामिति कहते हैं।

प्रश्न 2.
भारतीय गणितज्ञ आर्यभट्ट प्रथम का ज्यामिति के क्षेत्र में क्या योगदान है ?
उत्तर:
भारतीय गणितज्ञ आर्यभट्ट प्रथम ने समद्विबाहु त्रिभुज का क्षेत्रफल, पिरेमिड का आयतन, गोलों का आयतन आदि ज्ञात करने की विधि बताई थी।

प्रश्न 3.
रेखा किसे कहते हैं ?
उत्तर:
रेखा वह ज्यामितीय आकृति होती है जिसकी कोई मोटाई नहीं होती है, इसकी लम्बाई असीमित होती है अर्थात् यह दोनों ओर अनन्त तक बढ़ी हुई होती है।

प्रश्न 4.
स्वयंसिद्ध किसे कहते हैं?
उत्तर:
अनेक तथ्य इतने सरल एवं स्पष्ट होते हैं कि इन्हें अनुभव के आधार पर ही सत्य मान लिया जाता है। अतः ऐसे सरल एवं स्पष्ट सिद्धान्त जिनको बिना सिद्ध किए ही हम सत्य मान लेते हैं, स्वयंसिद्ध कहे जाते हैं । जैसे-एक राशि, दूसरी राशि के बराबर, बड़ी अथवा छोटी होती है।

प्रश्न 5.
अभिगृहीत किसे कहते हैं?
उत्तर:
ज्यामिति में ऐसी अनेक रचनाएँ होती हैं जिन्हें बिना प्रमाण के सत्य माना जाता है तथा इनके आधार पर अन्य ज्यामितीय रचनाओं या तथ्यों को सिद्ध किया जाता है, अभिगृहीत कहलाते हैं। जैसे-एक रेखाखण्ड को अपनी इच्छानुसार कितनी ही लम्बाई तक बढ़ाया जा सकता है।

प्रश्न 6.
यदि AB = PQ तथा PQ = xy तब दर्शाइए कि AB = xy
हल:
AB = PQ .....(i)
PQ = xy .....(ii)
जोड़ने पर
AB + PQ = PQ + xy 

दोनों तरफ PO घटाने पर
AB + PQ - PQ = PQ + xy – PQ
⇒ AB = xy इति सिद्धम्

लघूत्तरात्मक प्रश्न

प्रश्न 1.
यदि A, B और C एक रेखा पर स्थित तीन बिन्दु हैं और B बिन्दुओंA और C के बीच में स्थित है, तो सिद्ध कीजिए कि AB + BC = AC है।

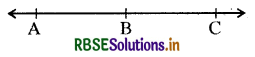
हल:
दी गई उपर्युक्त आकृति में AB + BC के साथ AC संपाती है। इसलिए यूक्लिड के अभिगृहीत 4 के अनुसार वे वस्तुएँ जो परस्पर संपाती हों, एक-दूसरे के बराबर होती हैं। इस अभिगृहीत के आधार पर यह सिद्ध किया जा सकता है कि AB + BC = AC

दिए गए प्रश्न के हल में यूक्लिड ने बिना कहीं बताए यह मान लिया है कि दो बिन्दुओं से होकर एक अद्वितीय रेखा खींची जा सकती है।

प्रश्न 2.
"सीधी रेखाओं के एक ऐसे युग्म का अस्तित्व है, जो एक-दूसरे से प्रत्येक स्थान पर समदूरस्थ होती हैं।" क्या यह कथन यूक्लिड की पाँचवीं अभिधारणा का एक प्रत्यक्ष (सीधा) परिणाम है ? स्पष्ट कीजिए।
हल:
एक रेखा l लीजिए और एक बिन्दु ऐसा लीजिए जो रेखा l पर स्थित न हो। तब प्लेफेयर अभिगृहीत के अनुसार, जो यूक्लिड की पाँचवीं अभिधारणा के समतुल्य है, हम जानते हैं कि P से होकर जाती हुई एक अद्वितीय रेखा m है जो l के समान्तर है।
अब, एक बिन्दु की एक रेखा से दूरी उस बिन्दु से रेखा पर डाले गए लम्ब की लम्बाई होती है। m पर स्थित किसी बिन्दु से रेखा l की दूरी और l पर स्थित किसी बिन्दु से रेखा m की दूरी सदैव समान होगी। अतः ये दोनों रेखाएँ l और m प्रत्येक स्थान पर एक-दूसरे से समदूरस्थ हैं।

प्रश्न 3.
दो भिन्न रेखाओं में एक से अधिक बिन्दु उभयनिष्ठ नहीं हो सकता।
हल:
यहाँ, हमें दो रेखाएँ l और m दी हुई हैं। हमें यह सिद्ध करना है कि l और m में केवल एक बिन्दु उभयनिष्ठ है। थोड़े समय के लिए, यह मान लीजिए कि ये दो रेखाएँ दो भिन्न बिन्दुओं P और Q पर प्रतिच्छेद करती हैं।
इस प्रकार, दो भिन्न बिन्दुओं P और Q से होकर जाने वाली आपके पास दो रेखाएँ l और m हो जाती हैं। परन्तु यह कथन अभिगृहीत 5.1 के विरुद्ध है, जिसके अनुसार दो भिन्न बिन्दुओं से होकर एक अद्वितीय रेखा खींची जा सकती है। अतः, हम जिस कल्पना से चले थे कि दो रेखाएँ दो भिन्न बिन्दुओं से होकर जाती हैं, गलत है।

प्रश्न 4.
निम्नलिखित में से कौनसे कथन सत्य हैं और कौनसे कथन असत्य हैं? अपने उत्तर के पक्ष में कारण दीजिए
(i) एक बिन्दु से केवल एक रेखा गुजरती है।
उत्तर:
असत्य

(ii) एक सांत रेखा अनिश्चित रूप से दोनों ओर बढ़ाई जा सकती है।
उत्तर:
सत्य

(iii) एक सांत रेखा एक ही ओर बढ़ाई जा सकती है।
उत्तर:
असत्य

(iv) दो भिन्न बिन्दुओं में से अनन्त रेखायें गुजरती हैं।
उत्तर:
असत्य

(v) वस्तुयें जो एक ही वस्तु के बराबर होती हैं, परस्पर भी बराबर होती हैं।
उत्तर:
सत्य

(vi) यदि दों वृत्त बराबर हों तो उनकी त्रिज्यायें भी बराबर होती हैं।
उत्तर:
सत्य

(vii) पूर्ण अपने भाग से छोटा होता है।
उत्तर:
असत्य

(viii) एक बिन्दु से किसी अन्य बिन्दु तक एक रेखा खींची जा सकती है।
उत्तर:
सत्य

प्रश्न 5.
रिक्त स्थानों की पूर्ति कीजिए
(i) यदि बराबरों से बराबर घटाया जाये तो ______________ भी बराबर होते हैं।
उत्तर:
शेषफल

(ii) तीन असरेख बिन्दुओं से ______________ रेखायें खींची जा सकती हैं।
उत्तर:
3

(iii) ______________ भिन्न बिन्दुओं से एक और केवल एक रेखा खींची जा सकती है।
उत्तर:
दो

(iv) वस्तुयें जो आपस में संपाती होती हैं, वे एक-दूसरे के ______________ होती हैं।
उत्तर:
बराबर

निबन्धात्मक प्रश्न

प्रश्न 1.
सिद्ध कीजिए कि एक दिए हुए रेखाखण्ड पर एक समबाहु त्रिभुज की रचना की जा सकती है।
हल:
उपर्युक्त कथन में, एक दी हुई लम्बाई का एक रेखाखण्ड, मान लीजिए, AB दिया है [देखिए आकृति (i)]।


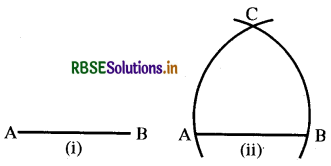
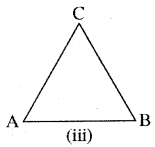
यहाँ आपको कुछ रचना करने की आवश्यकता है। यूक्लिड की अभिधारणा (3) का प्रयोग करके, आप बिन्दु A को केन्द्र और AB त्रिज्या लेकर एक वृत्त खींच सकते हैं [देखिए आकृति (ii)] । इसी प्रकार, B को केन्द्र मानकर और BA त्रिज्या लेकर एक अन्य वृत्त खींचा जा सकता है। ये दोनों वृत्त मान लीजिए बिन्दु C पर मिलते हैं। अब रेखाखण्डों AC और BC खींच कर AABC बनाइए [देखिए आकृति (iii)] 

इसलिए, आपको सिद्ध करना है कि यह त्रिभुज एक समबाहु त्रिभुज है; अर्थात् AB = AC = BC है। अब, AB = AC है, क्योंकि ये एक वृत्त की त्रिज्याएँ हैं। (1)
इसी प्रकार, AB = BC (एक ही वृत्त की त्रिज्याएँ) (2)
उपर्युक्त दोनों तथ्यों और यूक्लिड के पहले अभिगृहीत (वे वस्तुएँ जो एक ही वस्तु के बराबर होती हैं एक-दूसरे के बराबर होती हैं) से आप निष्कर्ष निकाल सकते हैं कि AB = BC = AC है। अतः, ΔABC एक समबाहु त्रिभुज है।
ध्यान दीजिए कि यहाँ यूक्लिड ने, बिना कहीं बताए, यह मान लिया है कि केन्द्रों A और B को लेकर खींचे गए वृत्त परस्पर एक बिन्दु पर मिलेंगे।