RBSE Class 9 Maths Important Questions Chapter 5 Introduction to Euclid’s Geometry

Rajasthan Board RBSE Class 9 Maths Important Questions Chapter 5 Introduction to Euclid’s Geometry Important Questions and Answers.

RBSE Class 9 Maths Chapter 5 Important Questions Introduction to Euclid’s Geometry

I. Multiple Choice Questions:
Choose the correct answer from the given options.

Question 1.
In ancient India, the shapes of altars used for household rituals were :
(a) squares and circles
(b) rectangles and squares
(c) triangles and rectangles
(d) trapeziums and pyramids
Answer:
(a) squares and circles

Question 2.
Euclid belongs to the country :
(a) India
(b) Greece
(c) Egypt
(d) Babylonia
Answer:
(b) Greece

Question 3.
The number of interwoven isosceles triangles in Sriyantra is :
(a) 11
(b) 9
(c) 8
(d) 7
Answer:
(b) 9

Question 4.
In Indus Valley Civilisation (about 300 BC) the bricks used for construction work were having dimensions in the ratio :
(a) 4 : 3 : 1
(b) 4 : 2 : 1
(c) 4 : 3 : 2
(d) 4:4:1
Answer:
(b) 4 : 2 : 1

Question 5.
Axioms are assumed :
(a) definitions
(b) theorems
(c) universal truths in all branches of mathematics
(d) universal truths specific to geometry
Answer:
(c) universal truths in all branches of mathematics

Question 6.
Euclid state that, "all right angles are equal to each other” in the form of:
(a) an axiom
(b) a definition
(c) a postulate
(d) a proof
Answer:
(a) an axiom

Question 7.
The number of dimensions, a point has:
(a) 0
(b) 1
(c) 2
(d) 3
Answer:
(a) 0

Question 8.
The number of dimensions, a solid has :
(a) 1
(b) 2
(c) 3
(d) 0
Answer:
(c) 3

Question 9.
It is known if x + y = 10 then x + y + z = 10 + z. The Euclid’s axiom that illustrates this statement is:
(a) first axiom
(b) second axiom
(c) third axiom
(d) fourth axiom
Answer:
(b) second axiom

Question 10.
Boundaries of solids are :
(a) surfaces
(b) curves
(c) lines
(d) points
Answer:
(a) surfaces

Question 11.
The number of dimensions, a plane surface has :
(a) 1
(b) 2
(c) 3
(d) 0
Answer:
(b) 2

Question 12.
Through two distinct points there:
(a) is no line that passes through them.
(b) is a unique line that passes through them.
(c) are two lines that pass through them.
(d) are more than two lines that pass through them.
Answer:
(b) is a unique line that passes through them.

Question 13.
Which of the following needs a proof?
(a) Theorem
(b) Axiom
(c) Definition
(d) Postulate
Answer:
(a) Theorem

Question 14.
A point C is said to lie between the points A and B, if:
(a) AC = CB
(b) AC + CB = AB
(c) points A, C and B are collinear
(d) None of these
Answer:
(c) points A, C and B are collinear

Question 15.
‘Lines are parallel if they do not intersect’ is stated in the form of:
(a) an axiom
(b) a definition
(c) a postulate
(d) a theorem
Answer:
(b) a definition

II. Fill in the Blanks:

Question 1.
If equals are added to equals, the ___________ are equal.
Answer:
wholes

Question 2.
A simple closed figure made up of three or more line segments is __________ .
Answer:
polygon

Question 3.
In Indus Valley Civilisation, the bricks used for construction work were having dimensions in the ratio __________ .
Answer:
4 : 2 : 1

Question 4.
The pyramid is a solid figure, the base of which is __________ .
Answer:
any polygon

Question 5.
Euclid divided his famous treatise “The Elements” into __________ chapters.
Answer:
13

III. True/False:
State whether the following statements are True or False.

Question 1.
A line has definite length.
Answer:
False

Question 2.
Shape of the altars were the combination of square and triangle.
Answer:
False

Question 3.
The Euclidean geometry is valid only for curved surface.
Answer:
False

Question 4.
The statements that are proved are called axiom.
Answer:
False

Question 5.
Euclid belongs to Greece.
Answer:
True

Question 6.
A line segment has two end points.
Answer:
True

Question 7.
Pythagoras was a student of Archimedes.
Answer:
False

IV. Match the columns:

Match the column I with the column II.

Column I	Column II
(1) Two distinct lines cannot	(i) be parallel to same line.
(2) Two distinct intersecting	(ii) ray
(3) Part of the line with two end points	(iii) have more than one point in common.
(4) Part of a line with one end point is	(iv) line segment

Answer:

Column I	Column II
(1) Two distinct lines cannot	(iii) have more than one point in common.
(2) Two distinct intersecting	(i) be parallel to same line.
(3) Part of the line with two end points	(iv) line segment
(4) Part of a line with one end point is	(ii) ray

V. Very Short Answer Type Questions:

Question 1.
Solve the equation x - 15 = 25 and state Euclid’s Axiom used here.
Answer:
We have, x - 15 = 25
⇒ x - 15 + 15 = 25 + 15
x = 40
Euclid’s Axiom (ii): If equals are added to equals, the wholes are equal.

Question 2.
Euclid divided the ‘elements’ into how many books?
Answer:
Euclid divided his famous treatise ‘elements’ into thirteen chapters, each called a book.

Question 3.
What are axioms?
Answer:
Axioms are the assumptions which are actually obvious universal truths in all branches of mathematics.

Question 4.
Look at the figure, and show that length AH > sum of lengths of AB + BC +CD.

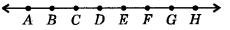
Answer:
We see that AB, BC and CD are parts of a line.
Now, AB + BC + CD = AD
By Euclid’s axiom 5, the whole is greater than the part, so
AH > AD
i,e., Length AH > sum of lengths of AB + BC + CD.
Hence Proved.

VI. Short Answer Type Questions:

Question 1.
If x + y = 10 and x = z, then show that z + y = 10.
Answer:
Given, x + y = 10 ........... (1)
and x = z ........... (2)
On subtracting y from both sides of equation (1), we get:
x + y - y = 10 - y (By axiom 3)
⇒ x = 10 - y
⇒ z = 10 - y (From equation 2)
On adding y both sides, we get:
z + y = 10 - y + y (By axiom 2)
⇒ z + y = 10
Hence Proved.

Question 2.
In the adjoining figure, if AB = AD and AC = AD, them prove that AB = AC. State Euclid’s axiom to support this.

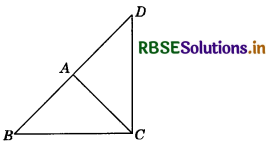
Answer:
Given, AB = AD
and AC = AD
∴ By Euclid’s first axiom: Two things equal to the same thing are equal to each other.
∴ AB = AC.

Question 3.
In figure, AC = XD, C is the mid-point of AB and D is the mid-point of XY. Using an Euclid’s axiom, show that AB = XY.

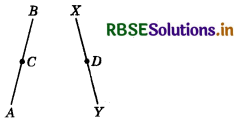
Answer:
AC = XD (Given)
⇒ 2AC = 2XD (∵Things which are double of the same thing are equal to one another.)
⇒ AB = XY (∵ C is the mid-point of AB and D is the mid-point of XY.)

Question 4.
In the given figure, AB = BC and BX = BY. Show that AX = CY. State the Euclid’s Axiom used.

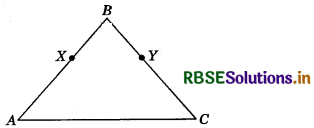
Answer:
We have,
AB = BC
⇒ AB - BX = BC - BX [If equals are subtracted from equals, the remainders are equal {Euclid’s Axiom (iii)}]
⇒ AB - BX = BC - BY
Hence, AX = CY (∵ BX = BY)

VII. Long Answer Type Questions:

Question 1.
In the adjoining figure, if QX = \(\frac{1}{2}\)XY, PX = \(\frac{1}{2}\)XZ and QX = PX, then show that XY = XZ.

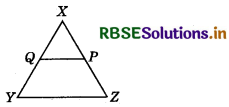
Answer:
Given, QX = \(\frac{1}{2}\)XY ........... (1)
PX = \(\frac{1}{2}\)XZ ......... (2)
and QX = PX
From equations (1), (2) and (3), we get:
\(\frac{1}{2}\)XY = \(\frac{1}{2}\)XZ
XY = XZ (By axiom 6)
Hence proved.

Question 2.
Read the following axioms:
(i) Things which are equal to the same things, are equal to one another.
(ii) If equals are added to equals, then wholes are equal.
(iii) Things which are double of the same things, are equal to one another.
Check whether the given system of axioms is consistent or inconsistent. 
Answer:
To check the given system consistent or inconsistent, we have to find whether we can deduce a statement from these axioms which contradicts any t axiom or not.
Some of Euclid’s axioms are :
(i) Things which are equal to the same things, are equal to one another.
(ii) If equals are added to equals, then wholes are equal.
(iii) Things which are double of the same things, are equal to one another.
Thus, given three axioms are Euclid’s axioms. So, here we cannot deduce any statement from these axioms which contradicts any axiom. So, given system of axioms is consistent.