RBSE Class 9 Maths Important Questions Chapter 4 दो चरों वाले रैखिक समीकरण

Rajasthan Board RBSE Class 9 Maths Important Questions Chapter 4 दो चरों वाले रैखिक समीकरण Important Questions and Answers.

RBSE Class 9 Maths Chapter 4 Important Questions दो चरों वाले रैखिक समीकरण

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
यदि y = 2x - 3 तथा y = 5 हो तो x का मान होगा
(A) 1
(B) 2
(C) 3
(D) 4
उत्तरः
(D) 4

प्रश्न 2.
यदि 2x + y = 6 हो तो इसको संतुष्ट करने वाला युग्म है
(A) (1, 2)
(B) (2, 1)
(C) (2, 2)
(D) (1, 1)
उत्तरः
(C) (2, 2)

प्रश्न 3.
यदि \(\frac{4}{x}\) + 5y = 7 तथा x = - \(\frac{4}{x}\) हो तो । का मान होगा
(A) 13
(B) 2
(C) \(\frac{1}{2}\)
(D) \(\frac{1}{3}\)
उत्तरः
(B) 2

प्रश्न 4.
यदि \(\frac{3}{x}\) + 4y = 5 तथा y = 1 हो तो x का मान होगा-
(A) 3
(B) \(\frac{1}{3}\)
(C) - 3
(D) -\(\frac{1}{3}\)
उत्तरः
(A) 3

प्रश्न 5.
यदि x = 1 हो तो समीकरण \(\frac{4}{x}+\frac{3}{y}\) = 5 में y का मान है
(A) 1
(B) \(\frac{1}{3}\)
(C) 3
(D) - 3
उत्तरः
(C) 3

प्रश्न 6.
x-अक्ष पर बिन्दु है
(A) (2, 3)
(B) (2, 0)
(C) (0, 2)
(D) (2, 2)
उत्तरः
(B) (2, 0)

प्रश्न 7.
यदि x = 2 हो, तो समीकरण x + \(\frac{y+2}{5}\) = 8 में y बराबर है
(A) 28
(B) 36
(C) 30
(D) 32
उत्तरः
(A) 28

प्रश्न 8.
समीकरण x + y = 6 और y - 2 = 2 में x बराबर होगा
(A) 8
(B) 4
(C) 6
(D) 2
उत्तरः
(D) 2

प्रश्न 9.
समीकरण \(\frac{y-3}{7}-\frac{x}{2}\) = 1 में यदि y = 10 हो, तो x बराबर है-
(A) 0
(B) 1
(C) - 2
(D) 2
उत्तरः
(A) 0

प्रश्न 10.
यदि (4, 20), समीकरण y = ax + 4 का एक हल है तब a =
(A) 3
(B) 4
(C) 5
(D) 6
उत्तरः
(C) 5

प्रश्न 11.
यदि (a, 7), 3x + y = 10 के ग्राफ पर स्थित है, तब a का मान है
(A) 3
(B) 1
(C) 2
(D) 4
उत्तरः
(B) 1

प्रश्न 12.
रैखिक समीकरण 2x + y = 4 का ग्राफ x-अक्ष को काटता है
(A) (2, 0) पर
(B) (-2, 0) पर
(C) (0, 4) पर
(D) (0, -4) पर
उत्तरः
(A) (2, 0) पर

प्रश्न 13.
रेखा x = 2 है
(A) x-अक्ष के समान्तर
(B) y-अक्ष के समान्तर
(C) मूल बिन्दु से गुजरने वाली रेखा
(D) इनमें से कोई नहीं
उत्तरः
(B) y-अक्ष के समान्तर

प्रश्न 14.
x = 5 एवं y = - 3 द्वारा कितने रैखिक समीकरण सन्तुष्ट होते हैं
(A) केवल एक
(B) दो
(C) तीन
(D) अनन्त
उत्तरः
(D) अनन्त

प्रश्न 15.
रेखाओं y = - 5 व 1 = 5 के मध्य की दूरी है
(A) 10
(B) 0
(C) - 10
(D) 1
उत्तरः
(A) 10

प्रश्न 16.
रेखाओं x = - 3 व x = 2 के मध्य की दूरी है
(A) 1
(B) 2
(C) 3
(D) 5
उत्तरः
(D) 5

प्रश्न 17.
यदि दो अंकों की संख्या में इकाई का अंक y व दहाई का अंक x हो तो संख्या होगी
(A) 10x + y
(B) 10x - y
(C) 10y + x
(D) 10y - x
उत्तरः
(A) 10x + y

प्रश्न 18.
0° सेल्सियस तापमान फारेनहाइट में होगा
(A) 30°F
(B) 32°F
(C) 34°F
(D) 38°F
उत्तरः
(B) 32°F

प्रश्न 19.
यदि 10x - 9y = 12 का एक हल (2k - 1, k) है, तब k =
(A) 1
(B) 2
(C) 3
(D) 4
उत्तरः
(B) 2

प्रश्न 20.
यदि रेखा 4x + 3y = 12 निर्देशांक अक्षों को A तथा B पर काटती है तब समकोण त्रिभुज AOB में कर्ण की लम्बाई होगी
(A) 4 इकाई
(B) 3 इकाई
(C) 5 इकाई
(D) 6 इकाई
उत्तरः
(C) 5 इकाई

प्रश्न 21.
x-अक्ष का समीकरण है
(A) y = 0
(B) x = 0
(C) x = 0, y = 0
(D) x = 2
उत्तरः
(A) y = 0

प्रश्न 22.
1-अक्ष का समीकरण है
(A) y = 0
(B) x = 0
(C) x = 0, y = 0
(D) x = 2
उत्तरः
(B) x = 0

प्रश्न 23.
रेखा का समीकरण, जो बिन्दु (25) से गुजरती है तथा x-अक्ष के समान्तर है
(A) x = 2
(B) x = 5
(C) y = 2
(D) y = 5
उत्तरः
(D) y = 5

प्रश्न 24.
रेखा का समीकरण, जो बिन्दु (3, - 5) से गुजरती है तथा y-अक्ष के समान्तर है
(A) x = 3
(B) x = - 5
(C) y = 3
(D) y = - 5
उत्तरः
(A) x = 3

प्रश्न 25.
रेखा 2y - 1 = y + 1 है
(A) x-अक्ष के लम्बवत्
(B) x-अक्ष को काटने वाली
(C) y-अक्ष के लम्बवत्
(D) मूल बिन्दु से जाने वाली
उत्तरः
(C) y-अक्ष के लम्बवत्

रिक्त स्थानों की पूर्ति करो

प्रश्न 1.
ax + by + c = 0 के रूप के समीकरण को, जहाँ a, b और c वास्तविक संख्याएँ हैं और a और b दोनों शून्य नहीं हैं, दो चरों वाला ....................... समीकरण कहते हैं।
उत्तरः
रैखिक

प्रश्न 2.
दो चरों वाले रैखिक समीकरण के अपरिमित रूप से अनेक .............................. होते हैं।
उत्तरः
हल

प्रश्न 3.
दो चरों वाले प्रत्येक रैखिक समीकरण का आलेख एक .............................. होता है।
उत्तरः
सरल रेखा

प्रश्न 4.
....................., y-अक्ष का समीकरण है और ........................., x-अक्ष का समीकरण है।
उत्तरः
x = 0, y = 0

प्रश्न 5.
x = a का आलेख .................................. के समान्तर एक सरल रेखा है।
उत्तरः
y-अक्ष

प्रश्न 6.
रेखा 2x + 3y = 6, x-अक्ष को ............................ और -अक्ष को ............................... पर काटती है।
उत्तरः
(3, 0) और (0, 2)

प्रश्न 7.
y = mx प्रकार की रेखा सदैव ............................. से होकर जाती है।
उत्तरः
मूल बिन्दु

प्रश्न 8.
रेखा y = 1 सदैव ........................... के समान्तर रेखा है।
उत्तरः
x-अक्ष

सत्य/असत्य-निम्नलिखित कथनों के लिए सत्य अथवा असत्य लिखिए

प्रश्न 1.
यदि (4, 20) समीकरण y = ax + 4 का एक हल है तब a = 6 है।
उत्तर:
असत्य

प्रश्न 2.
यदि (a, 7), रेखा 3x + y = 10 के ग्राफ पर स्थित है, तब a का मान 1 है।
उत्तर:
सत्य

प्रश्न 3.
रैखिक समीकरण 2x + y = 4 का ग्राफ x-अक्ष को बिन्दु (-2, 0) पर काटता है।
उत्तर:
असत्य

प्रश्न 4.
x = 5 एवं y = - 3 द्वारा अनन्त रैखिक समीकरण सन्तुष्ट होते हैं।
उत्तर:
सत्य

प्रश्न 5.
रेखाओं y = - 5 एवं y = 5 के मध्य की दूरी शून्य है।
उत्तर:
असत्य

प्रश्न 6.
रेखाओं x = - 3 एवं x = 2 के मध्य की दूरी 5 है।
उत्तर:
सत्य

प्रश्न 7.
यदि दो अंकों की संख्या में इकाई का अंक ) व दहाई का अंक x हो तो वह संख्या 10x + y होगी।
उत्तर:
सत्य

प्रश्न 8.
x = 5, उस रेखा का समीकरण है, जो बिन्दु (2, 5) से गुजरती है तथा x-अक्ष के समान्तर है।
उत्तर:
असत्य

असत्य अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
समीकरण 5y - 3x - 10 = 0 में y को x के रूप में व्यक्त कीजिए। वह बिन्दु ज्ञात कीजिए जहाँ समीकरण 5y - 3x – 10 = 0 द्वारा निरूपित रेखा y-अक्ष को काटती है।
हल:
समीकरण 5y - 3x – 10 = 0
5y = 3x + 10
y = \(\frac{3 x+10}{5}\)
समीकरण 5y - 3x - 10 = 0 में रेखा y-अक्ष पर तब काटेगी जब x = 0 होगा तो y = \(\frac{3 \times 0+10}{5}\) = 2 अतः वह बिन्दु (0, 2) होगा।

प्रश्न 2.
यदि दो अंकों वाली एक संख्या में इकाई का अंक b तथा दहाई का अंक a हो तो संख्या लिखिए।
हल:
संख्या (10a + b) होगी।

प्रश्न 3.
एक संख्या x का दुगुना से 24 अधिक है। इस वाक्य को प्रकट करने वाला समीकरण लिखिए।
हल:
2x - y = 24

प्रश्न 4.
राम की आयु x वर्ष तथा श्याम की आयु । वर्ष है। पाँच वर्ष पूर्व राम की आयु श्याम की आयु की | दुगुनी थी। इस कथन को प्रकट करने वाले समीकरण को ax + by + c = 0 के रूप में लिखिए। हल:
राम श्याम
(x - 5) = 2(y - 5)
x - 5 = 2y - 10
⇒ x - 5 + 2 + 10 = 0
⇒ x + 2 + 5 = 0

प्रश्न 5.
दो संख्याओं का योग 10 और अंतर 4 है, तो उनमें बड़ी संख्या को ज्ञात कीजिए।

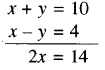
∴ x = \(\frac{14}{2}\) = 7

प्रश्न 6.
यदि एक भिन्न के अंश और हर में 1 जोड़ते हैं तो भिन्न का मान \(\frac{1}{2}\) हो जाता है। इसे समीकरण में कैसे लिखेंगे?
हल:
माना भिन्न \(\frac{x}{y}\) है।
\(\frac{x+1}{y+1}=\frac{1}{2}\)

प्रश्न 7.
समीकरण 3x - 27+7 = 0 में x का मान 5 हो तो y का मान ज्ञात कीजिए।
हल:
3 × 5 - 2y + 7 = 0
या 2y = 15 + 7
या y = \(\frac{22}{2}\) = 11
अतः y = 11

प्रश्न 8.
समीकरण 2x + y = 3 में y का मान 7 हो तो x का मान ज्ञात कीजिए।
हल:
2x + y = 3
2x + 7 = 3 या 2x = 3 - 7
या x = \(\frac{-4}{2}\) = - 2
x = -2

प्रश्न 9.
समीकरण x - y = 0 में x का मान 2 हो तो y का मान ज्ञात कीजिए।
हल:
x - y = 0
या 2 - y = 0 या y = 2

प्रश्न 10.
p का मान लिखिए जबकि x = 3, y = - 2 समीकरण 5x + 6y = p को सन्तुष्ट करते हों।
हल:
दिया समीकरण
5x + 6y = p
∴ 5 × 3 + 6 × (-2) = p
15 - 12 =p
∴ p = 3

प्रश्न 11.
यदि किसी संख्या के 5 गुने में 10 जोड़ा जाये, तो वह 25 के बराबर हो जाती है। इस कथन को समीकरण के रूप में लिखिए।
हल:
माना वह संख्या = x है।
प्रश्नानुसार 5x + 10 = 25

प्रश्न 12.
यदि आपको एक रैखिक समीकरण दी गई हो तो उसे आप कैसे पहचानोगे? उदाहरण दीजिए।
हल:
रैखिक समीकरण में चर की अधिकतम घात एक होगी एवं उस रैखिक समीकरण का ग्राफ खींचने पर एक सीधी रेखा प्राप्त होगी।
जैसे- 3x + 2y = 10
और y + 5x = 0 आदि
रैखिक समीकरण के उदाहरण हैं।

लघूत्तरात्मक प्रश्न

प्रश्न 1.
निम्नलिखित सेल्सियस को फारेनहाइट में रूपान्तरित कीजिए--
(i) 50°C
(ii) 60°C
(iii) 0°C
हल:
(i) 50°C हम जानते हैं, सम्बन्ध
F = \(\frac{9}{5}\)C + 32 होता है।
मान रखने पर
F = \(\frac{9}{5}\) × 50 + 32
= 9 × 10 + 32
= 90 + 32
= 122°F

(ii) 60°C
F = \(\frac{9}{5}\)C + 32
मान रखने पर
F = \(\frac{9}{5}\) × 60 + 32
= 9 × 12 + 32
= 108 + 32 = 140°F

(iii) 0°C
F = \(\frac{9}{5}\)C + 32
मान रखने पर
F = \(\frac{9}{5}\) × 0 + 32
= 0 + 32 = 32°F

प्रश्न 2.
यदि बिन्दु (6,-5) समीकरण 6y = mx - 9 के आलेख पर स्थित है, तो m का मान ज्ञात कीजिए।
हल:
बिन्दु (6, - 5) आलेख पर स्थित है तो समीकरण
6y = mx - 9 को सन्तुष्ट करना चाहिए।
∴ 6 × (-5) = m × 6 - 9
या -30 = 6m - 9
या -30 + 9 = 6m
या - 21 = 6m
⇒ - 6m = - 21
m = \(\frac{-21}{6}\) = \(\frac{-7}{2}\) 

प्रश्न 3.
निम्नलिखित समीकरणों में से प्रत्येक के दो हल ज्ञात कीजिए
(i) 4x + 3y = 24
(ii) 7x + 9y = 0
हल:
(i) x = 0 लेने पर
4 × 0 + 3y = 24
⇒ 0 + 3y = 24
⇒ 3y = 24
∴ y = \(\frac{24}{3}\)
y = 8
अतः (0, 8) समीकरण का हल है।
y = 0 लेने पर
4x + 3 × 0 = 24
⇒ 4x + 0 = 24
4x = 24
∴ y = \(\frac{24}{4}\)
x = 6
अतः (6, 0) समीकरण का हल है।
समीकरण 4x + 3y = 24 के दो हल (0, 8) और (6, 0) होंगे।

(ii) x = 0 लेने पर,
7 × 0 + 9y = 0
0 + 9y = 0
9y = 0
∴ y = 0
अतः (0, 0) समीकरण का हल है। y = 0 लेने पर
7x + 9 × 0 = 0
7x+ 0 = 0
7x = 0
x = 0
∴ (0, 0) पुनः समीकरण का हल है।
x = 1 लेने पर
7 × 1 + 9y = 0
7 + 9y = 0
9y = 0 - 7 = - 7
⇒ y = \(\frac{-9}{7}\)
अतः (1, - \(\frac{-9}{7}\)) समीकरण का हल है।
अतः दिये गये समीकरण के दो हल (0, 0) और (1, -\(\frac{-9}{7}\)) होंगे।

प्रश्न 4.
निम्नलिखित में से प्रत्येक का आलेख खींचिए
(a) x = 2
(b) x = - 1
(c) y = -3
(d) 2y + 5 = 0
(e) 3r - 2 = 0
(f) x + y = 0
(g) x - y = 0
(h) x = 0
(i) y = 0.
हल:
(a) x = 2 में
'y' की अनुपस्थिति यह प्रकट करती है कि भुजा 'x' चर y' पर आश्रित नहीं है। इसका अर्थ यह है कि कोटि v का कोई भी मान हो भुजा 'x' का मान 2 ही रहेगा। इस प्रकार हमें निम्नलिखित सारणी प्राप्त होती है|

इन बिन्दुओं को आलेखित करने और रूलर से | मिलाने पर हमें रेखा x = 2 से (l से निर्धारित) प्राप्त होती है जो y-अक्ष के समान्तर है।

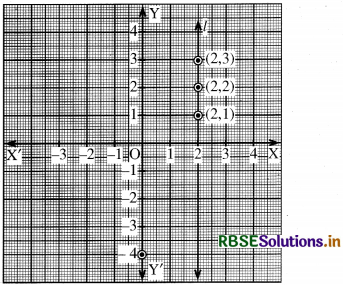
(b) x = - 1
x = - 1; का आलेख -अक्ष के समान्तर है और y-अक्ष के बायीं ओर 1 एकक की दूरी पर है।

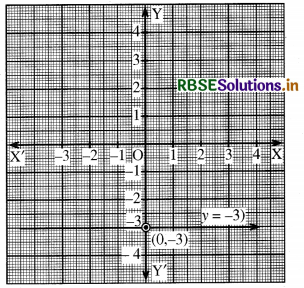
(c) y = - 3
y = - 3 का आलेख x-अक्ष के समान्तर रेखा है और x-अक्ष से नीचे की ओर 3 एकक की दूरी पर है। चूँकि x-अक्ष के नीचे y का मान ऋणात्मक होता है।

(d) 2y + 5 = 0
⇒ y = - \(\frac{5}{2}\)
2y + 5 = 0 का आलेख एक रेखा है जो x-अक्ष के समान्तर है और X-अक्ष से नीचे की ओर 2.5 एकक की दूरी पर है।

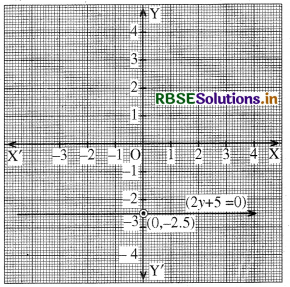
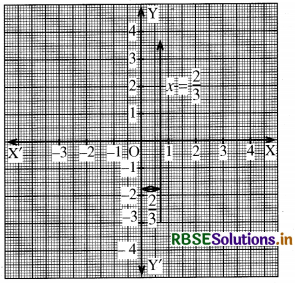
(e) 3x - 2 = 0
⇒ 3x = 2
⇒ x = \(\frac{2}{3}\)
माना कि 1 एकक = 6 भाग
∴ \(\frac{2}{3}\) एकक = 6 × \(\frac{2}{3}\) = 4 भाग
3x - 2 = 0; का आलेख एक रेखा है जो 7-अक्ष के दायीं ओर \(\frac{2}{3}\) एकक की दूरी पर है।

(f) x + y = 0
y = - x
x के मानों के संगत y के मानों को प्रदर्शित करती सारणी इस प्रकार है-

इन बिन्दुओं को आलेखित करके हमें आलेख प्राप्त होता है-
पैमाना: X-अक्ष पर 1 सेमी. = 1 इकाई
Y-अक्ष पर 1 सेमी. = 1 इकाई

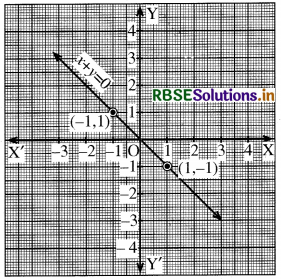
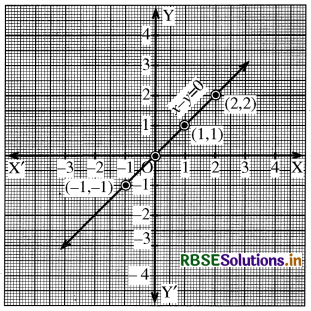
(g) x - y = 0
⇒ x = y
या y = x
x के मानों के संगत y के मानों को प्रदर्शित करती सारणी इस प्रकार है-

इन बिन्दुओं को आलेखित करके हमें आलेख प्राप्त होता है-
पैमाना-X-अक्ष पर 1 सेमी. = 1 इकाई
Y-अक्ष पर 1 सेमी. = 1 इकाई

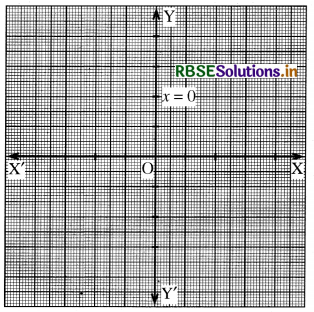
(h) x = (0 संकेत करता है कि यह y-अक्ष की समीकरण है।
∴ प्राप्त आलेख है-

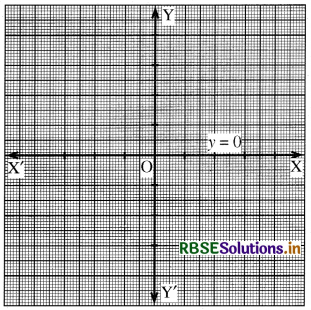
(i) y = 0 संकेत करता है कि यह x-अक्ष की समीकरण है।
∴ प्राप्त आलेख है-

निबन्धात्मक प्रश्न

प्रश्न 1.
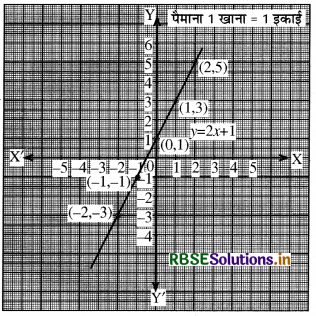
x के मान x = - 2 से x = 2 के मध्य लेते हुए समीकरण y = 2x + 1 के मानों से सारणी का निर्माण कीजिए तथा उक्त समीकरण का आलेख खींचिए।
हल:
समीकरण y = 2x + 1

प्रश्न 2.
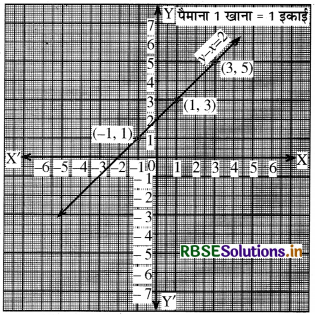
समीकरण y - x = 2 का आलेख खींचिए।
हल:
प्रश्नानुसार - x = 2
⇒ y = x + 2
यदि x = 1, तो y = 1 + 2 = 3
यदि x = 3, तो y = 3 + 2 = 5
यदि x = - 1 तो y = - 1 + 2 = 1
इस प्रकार उक्त बिन्दुओं के आधार पर आलेख खींचने के लिए निम्न सारणी प्राप्त होगी-

ग्राफ पेपर पर वांछित पैमाना, x-अक्ष पर 1 सेमी. = 1 इकाई तथा y-अक्ष पर 1 सेमी = 1 इकाई, मानने पर निम्नानुसार आलेख प्राप्त होगा-

प्रश्न 3.
समीकरण x - 2y = 3 का आलेख खींचिए तथा यदि
(i) x = -5
(ii) y = 0 हो तो निर्देशांक ज्ञात कीजिए।
हल:
प्रश्नानुसार x - 2y = 3
⇒ y = \(\frac{x-3}{2}\)
यदि x = 1, तो y = \(\frac{1-3}{2}=\frac{-2}{2}\) = - 1
यदि x = - 1, तो y = \(\frac{-1-3}{2}=\frac{-4}{2}\) = - 2
इस प्रकार हमें निम्नलिखित सारणी प्राप्त होती है-

ग्राफ पेपर पर बिन्दुओं (1, - 1) तथा (- 1, - 2) को आलेखित कर मिलाने पर समीकरण x - 2y = 3 का निम्नांकित ग्राफ प्राप्त होता है-

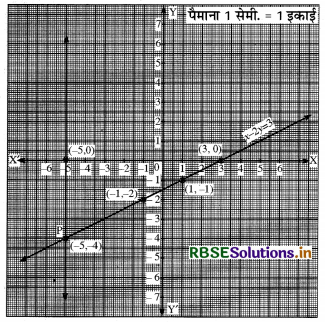
यदि x = - 5 हो तो निर्देशांक प्राप्त करने के लिए y-अक्ष के समान्तर एक रेखा खींची जो (-5, 0) से गुजरे। यह रेखा समीकरण x - 2y = 3 से प्राप्त ग्राफ पर एक बिन्दु P (-5, -4) पर मिलती हैं। अब वहाँ से x-अक्ष के समान्तर एक रेखा खींची जो y-अक्ष पर y = -4 पर मिलती है। अतः इस वांछित बिन्दु के निर्देशांक (-5, -4) हैं।

तथा यदि y = 0, x-अक्ष पर हो तो x-अक्ष पर मिलने वाली रेखा का ही बिन्दु होगा। ग्राफ के अनुसार इस बिन्दु के निर्देशांक (3, 0) हैं। अत: निर्धारित बिन्दु (-5, - 4) तथा (3, 0) होंगे।

प्रश्न 4.
समीकरण 2x + 3y = 5 का आलेख खींचिए तथा जाँच कीजिए कि क्या बिन्दु (-3, 4) तथा (7, - 3) दिये गये समीकरण के हल हैं? .
हल:
दिया गया समीकरण
2x + 3y = 5
3y = 5 - 2x
y = \(\frac{5-2 x}{3}\)

पैमाना: X-अक्ष पर 1 सेमी. = 1 इकाई
Y-अक्ष पर 1 सेमी = 1 इकाई

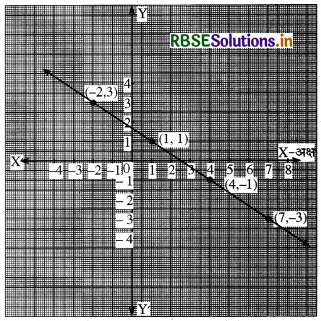
अतः निर्देशांक बिन्दु होंगे (1, 1), (4, - 1) तथा (-2, 3) ग्राफ पर आलेखित करने पर ग्राफ से स्पष्ट है कि बिन्दु (7, - 3) ग्राफ रेखा पर स्थित है और बिन्दु (-3, 4) ग्राफ पर स्थित नहीं है। अतः बिन्दु (7, - 3) दिये गये समीकरण के हल हैं।