RBSE Class 9 Maths Important Questions Chapter 4 Linear Equations in Two Variables

Rajasthan Board RBSE Class 9 Maths Important Questions Chapter 4 Linear Equations in Two Variables Important Questions and Answers.

RBSE Class 9 Maths Chapter 4 Important Questions Linear Equations in Two Variables

I. Multiple Choice Questions :
Choose the correct answer from the given options.

Question 1.
The number of lines passing through a point (2, 3) are :
(a) only one
(b) two
(c) infinite
(d) None of these
Answer:
(c) infinite

Question 2.
Which of the following are solutions of the equation x + 2y = 7?
(a) x = 3, y = 5
(b) x = 3, y = - 5
(c) x = 3, y = 2
(d) x = 0, y = 7
Answer:
(c) x = 3, y = 2

Question 3.
The graph of equation 2x + 3y = 12 represents a :
(a) point
(b) straight line
(c) triangle
(d) square
Answer:
(b) straight line

Question 4.
The graph of equation 3x + 4y = 12 intersects -e-axis at :
(a) (4, 0)
(b) (0, 3)
(c) (4, 3)
(d) (0, 0)
Answer:
(a) (4, 0)

Question 5.
The graph of y = b is a straight line :
(a) parallel to x-axis
(b) parallel to y-axis
(c) passes through origin
(d) coincident on x-axis
Answer:
(a) parallel to x-axis

 

Question 6.
x = 5, y = 2 is a solution of the linear equation :
(a) x + 2y = 7
(b) 5x + 2y = 7
(c) x + y = 7
(d) 5x + y = 7
Answer:
(c) x + y = 7

Question 7.
Any point on the fine y = x is of the form :
(a) (a, a)
(b) (0, a)
(c) (a, 0)
(d) (a, - a)
Answer:
(a) (a, a)

Question 8.
The number of linear equations in x and y which can be satisfied by x = 1 and y = 2 (are) :
(a) only one
(b) two
(c) three
(d) infinitely many
Answer:
(d) infinitely many

Question 9.
The graph of the linear equation y = x passes through the point :
(a) \(\left(\frac{3}{2},-\frac{3}{2}\right)\)
(b) (0, \(\frac{3}{2}\))
(c) (1, 1)
(d) \(\left(-\frac{1}{2}, \frac{1}{2}\right)\)
Answer:
(c) (1, 1)

Question 10.
The equation 2x + 5y = 7 has unique solution of x, y are :
(a) natural numbers
(b) positive real numbers
(c) real numbers
(d) rational numbers
Answer:
(a) natural numbers

Question 11.
The equation y + 3 = 0 represents a line :
(a) parallel of y-axis
(b) parallel to x-axis
(c) passing through origin
(d) passing through the point (- 3, 0)
Answer:
(b) parallel to x-axis

Question 12.
Which of the following equations represents a line parallel to x-axis?
(a) 3x + 2 = 0
(b) 3y + 2 = 0
(c) 3x + 2y = 0
(d) 3x - 2y = 0
Answer:
(b) 3y + 2 = 0

Question 13.
The equation x = 2y represents a line :
(a) parallel to x-axis
(b) parallel to y-axis
(c) passing through origin
(d) passing through the point (1, 2)
Answer:
(c) passing through origin

Question 14.
Which of the following equations has a graph shown in the adjoining figure?

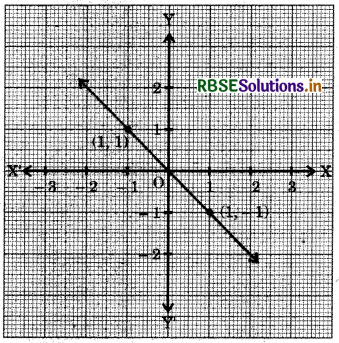
(a) y = x
(b) x + y = 0
(c) y = 2x
(d) 2 + 3y = 7x
Answer:
(b) x + y = 0

Question 15.
Choose the equation whose graph is represented below:

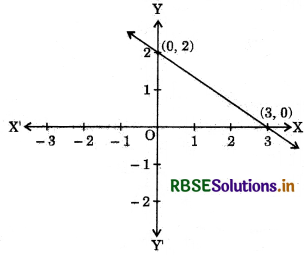
(a) 2x + 3y = 7
(b) 2x + 3y = 9
(c) 2x + 3y = 6
(d) x + y = 2
Answer:
(c) 2x + 3y = 6

II. Fill in the Blanks :

Question 1.
If the linear equation 3x - ay = 6 has one solution as (4, 3), then a = ______________.
Answer:
2

Question 2.
If the point (3, 4) lies on the graph of 3y = ax + 7, then the value of a = ______________
Answer:
\(\frac{5}{3}\)

Question 3.
The solution of the linear equation x + 2y = 8, which represents a point on x-axis ______________
Answer:
(8, 0)

Question 4.
The equation of the x-axis is given by ______________
Answer:
y = 0

Question 5.
The linear equation for the statement “Age of ‘x’ exceeds age of y by 7 years” = ______________
Answer:
x - y - 7 = 0

III. True/ False:
State whether the following statements are True or False.

Question 1.
ax + by + c = 0, where a, b and c are real numbers, is a linear equation in two variables.
Answer:
False

Question 2.
The graph of the equation y = 3x + 5 passes through the origin.
Answer:
False

Question 3.
The line parallel to the x-axis at distance 3 units above x-axis is given by the line y = 3.
Answer:
False

Question 4.
The graph of every linear equation in two variables need not be a straight line.
Answer:
True

Question 5.
Every point on the graph of a linear equation in two variables does not represent a solution of the linear equation.
Answer:
False

Question 6.
The graph of the equation y = 1 is a line parallel to y-axis.
Answer:
False

Question 7.
A linear equation in two variables has no more than two solutions.
Answer:
False

Question 8.
The graph of the line y = -2 is parallel to x-axis at a distance of 2 units below the origin.
Answer:
True

IV. Match the Columns :

Question 1.
Match the column I with the column II.

Column I	Column II
1. If the point (1,2) lies on the line 2x + ay = 8 then a =	1
2. The number of solutions of the equation x + 5y = 11 where x, y are natural number is (are)	2
3. The number of lines passing through (3, 4) and parallel to x-axis is (are)	3

Answer:

Column I	Column II
1. If the point (1,2) lies on the line 2x + ay = 8 then a =	3
2. The number of solutions of the equation x + 5y = 11 where x, y are natural number is (are)	2
3. The number of lines passing through (3, 4) and parallel to x-axis is (are)	1

V. Very Short Answer Type Questions :

Question 1.
Find the value ‘m’ if (- m, 3) is a solution of equation 4x + 9y - 3 = 0.
Answer:
If (- m, 3) is a solution of the equation
4x + 9y - 3 = 0, then 4(- m) + 9(3) -3 = 0
⇒ - 4m + 27 - 3 = 0
⇒ - 4m + 24 = 0
⇒ 4m = 24
⇒ m = \(\frac{24}{4}\) = 6

Question 2.
Give the equations of two lines passing through (3, 14). How many more such lines are there, and why?
Answer:
The equations of two lines passing through (3, 14) can be taken as
x + y = 17 and 7x - y = 7
There are infinitely many such fines because through a point an infinite number of fines can be drawn.

Question 3.
If the point (3, 4) lies on the graph of the equation = ax + 7, find the value of a.
Answer:
8y = ax + 7, then
8(4) = a(3) + 7
⇒ 32 = 3a + 7
⇒ 32 - 7 = 3a
⇒ 25 = 3a
⇒ 3a = 25
⇒ a = \(\frac{25}{3}\)

Question 4.
Express the linear equation 7 = 2x in the form ax + by + c = 6 and also write the values of a, b and c.
Answer:
7 = 2x
⇒ 2x - 7 = 0
⇒ 2x + 0y-7 = 0 .
Comparing with ax + by + c = 0, we get :a = 2, 6 = 0, c = - 7

Question 5.
Write two solutions of the linear equation x + 2y = 1.
Answer:
x + 2y = 1
⇒ 2y = 1 - x
⇒ y = \(\frac{1-x}{2}\)
When x = 1 , y = \(\frac{1-1}{2}\) = 0
When x = 3, y = \(\frac{1-3}{2}=\frac{-2}{2}\) = -1
Two solution are (1, 0); (3, -1)

Question 6.
The cost of a pen is ₹ 5 less than half the cost of a notebook. Write this statement as a linear equation in two variables.
Answer:
Let the cost of notebook be x and cost of pen be y.
∴ According to the given condition
y = \(\frac{1}{2}\)x - 5
2y = x - 10
⇒ x - 2y - 10 = 0 is the linear equation in two variables.

VI. Short Answer Type Questions :

Question 1.
Determine the point on the graph of the linear equation 2x + 5y = 19, whose ordinate is lg times its abscissa.
Answer:
Let x and y be the abscissa and ordinate, respectively of the point lie on given line 2x + 5y = 19. ...............(i)
Then, by given condition,
Ordinate (y) = 1\(\frac{1}{2}\)x (Abscissa) ...............(ii)
⇒ y = \(\frac{3}{2}\)x

On putting y = \(\frac{3}{2}\)x in equation (i), we get:
2x + 5 (\(\frac{3}{2}\)) = 19
⇒ 4x + 15x = 38
⇒ 19x = 38
⇒ x = 2

On substituting the value of * in equation (ii), we get:
y = \(\frac{3}{2}\) × 2 = 3
Hence, the required point is (2, 3).

Question 2.
Let y varies directly as x. If y = 12 when x = 4, then write a linear equation. What is value of y when x = 5?
Answer:
Given that, y varies directly as x.
i.e. y ∝ x ⇒ y = kx .............(i)
Where, k is an arbitrary constant.
Given, y = 12 and x = 4
Then, from equation (i),
12 = 4k
⇒ k = 3
On putting the value of k in equation (i), we get:
y = 3x .............(ii)
Which is the required linear equation.
When x = 5, then from equation (ii),
y = 3 × 5 = 15

Question 3.
Compare the; equation \(\frac{x}{3}+\frac{3}{2}\)y + 4 = 2y - 3 and lx + my - n = 0 and write the value of l, m and n.
Answer:
\(\frac{x}{3}+\frac{3}{2}\)y + 4 = 2y - 3
\(\frac{x}{3}+\frac{3}{2}\)y + 7 = 0
Comparing with lx + my - n = 0, we get: l = \(\frac{1}{3}\)x,m = - \(\frac{1}{2}\),n = -7

Question 4.
Find at least 3 solutions for the following linear equation in two variables: 2x + 5y = 13
Answer:
2x + 5y = 13
⇒ 5y = 13 - 2x
⇒ y = \(\frac{13-2 x}{5}\)
Put x = 0, then y = \(\frac{13-2(0)}{5}=\frac{13}{5}\)
Put x = 1, then y = \(\frac{13-2(1)}{5}=\frac{11}{5}\)
Put x = 2, then y = \(\frac{13-2(2)}{5}=\frac{9}{5}\)
Put x = 3, then y = \(\frac{13-2(3)}{5}=\frac{7}{5}\)
∴ (0, \(\frac{13}{5}\)), (1, \(\frac{11}{5}\)), (2, \(\frac{9}{5}\)) and (3, \(\frac{7}{5}\)) are the solutions of the equation 2x + 5y = 13.

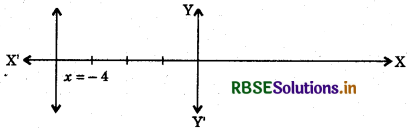
Question 5.
How many solutions of the equation 2x + 1 = x - 3 are there on the :
(i) number line?
(ii) cartesian plane?
Answer:
2x + 1 = x - 3
2x - x = - 1 - 3
x = - 4
(i) On number line, only one solution is possible i.e. x = - 4

(ii) On cartesian plane.
We have solutions as :
x + 0.y + 4 = 0 ..........(i)

At y = 1, y = 2, and y = 3, are x = -4, x = -4, x = 4. [from(i)]

∴ In cartesian plane infinitely many solutions are possible for x + O.y + 4 = 0. The graph is a line parallel to y-axis at a distance of - 4 units to the left of origin.

Question 6.
Solve for x : 3x - 12 + \(\frac{3}{7}\)x = 2(x - 1)
What type of graph is it in two dimensions?
Answer:
3x - 12 + \(\frac{3}{7}\)x = 2(x - 1) 94
⇒ \(\frac{24}{7}\)x - 12 = 2x - 2
⇒ \(\frac{24}{7}\)x - 2x = 12 - 2
⇒ \(\frac{10 x}{7}\) = 10
⇒ x = 7
The graph of this equation is a line parallel to y-axis at a distance of 7 units to the right of origin O.

VII. Long Answer Type Questions :

Question 1.
Give the geometrical representation of 2y + 7 = 0 as equation in :
(i) one variable,
(ii) two variables.
Answer:
The given equation is
2y + 7 = 0

(i) In one variable
2y + 7 = 0
⇒ 2y = - 7
⇒ y = -\(\frac{7}{2}\)
The representation of y = \(\frac{7}{2}\) on the number line is as shown fig. :

(ii) In two variables
2y + 7 = 0
0.x+2.y+7 = 0
It is a linear equation in two variables x and y. This is represented by a line. All the values of x are possible because O.x is always O. However, y must satisfy the relation 2y + 7 = 0,

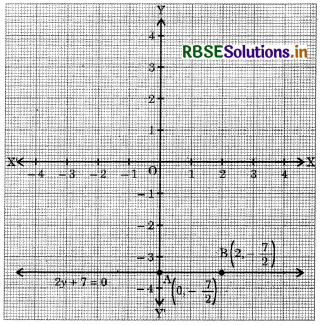
i.e. y = -\(\frac{7}{2}\). Hence, two solutions of the given equation are x = 0, y = -\(\frac{7}{2}\) and x = 2, y = -\(\frac{7}{2}\).

Thus, the graph AB is a line parallel to the x-axis at a distance of units below it.

Question 2.
Force applied on a body is directly proportional to the acceleration produced in the body. Write an equation to express the situation and plot the graph of the equation taking constant to he 5 units.
Answer:
Let the force applied on a body be y units and the acceleration produced in the body be a units.

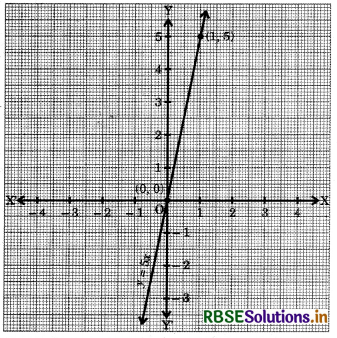
Then,
y ∝ x
⇒ y = kx
Here, k = 5 units (given)
∴ y = 5x ...............(1)

(1) is an equation to express the situation.
Table of solutions

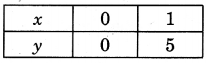
We plot the points (0, 0) and (1, 5) on a graph paper and join the same by a ruler to get the line which is the graph of the equation y = 5x.

Question 3.
Draw the graph of the linear equation y = mx + c for m = 2 and c = 1. Read from the graph, the value of y when x = \(\frac{3}{2}\).
Answer:
Given equation is y = mx + c.
For m = 2 and c = 1, the linear equation is y = 2x + 1 ................(i)

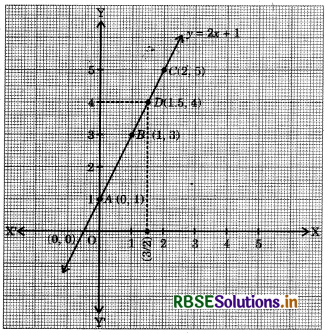
When x = 0, then y = 2 × 0 + 1 = 1
When x = 1, then y = 2 × 1 + 1 = 3
When x = 2, then y = 2 × 2 + 1 = 5

Thus, we have the following table :

So, plot the points A(0,1), 5(1, 3) and C(2, 5) on the graph paper and join them by a line.
Thus, the line AC is the required graph of given linear equation.

Now, draw a line parallel to Y-axis at a g distance x = \(\frac{3}{2}\) from O on X-axis. The line intersects the graph AC at point D. Now, draw a perpendicular from D on Y-axis, which intersects at y = 4.
Hence, it is clear from the graph that when x = \(\frac{3}{2}\) then y = 4.