RBSE Class 9 Maths Important Questions Chapter 3 Coordinate Geometry

Rajasthan Board RBSE Class 9 Maths Important Questions Chapter 3 Coordinate Geometry Important Questions and Answers.

RBSE Class 9 Maths Chapter 3 Important Questions Coordinate Geometry

I. Multiple Choice Questions:
Choose the correct answer from the given four options.

Question 1.
Point (- 10, 0) lies:
(a) on the negative direction of X-axis.
(b) in the third quadrant,
(c) on the negative direction of Y-axis.
(d) in the fourth quadrant.
Answer:
(a) on the negative direction of X-axis.

Question 2.
Signs of abscissa and ordinate of a point in the second quadrant are respectively:
(a) +, +
(b) -, -
(c) -, +
(d) +, -
Answer:
(c) -, +

Question 3.
Which of the following points lie in the IVth quadrant?
(a) (-2, 0)
(b) (- 3, 2)
(c) (4, -7)
(d)(-3, -5)
Answer:
(c) (4, -7)

Question 4.
If P(- 1, 1), Q(3, - 4), R(1, - 1), S(-2, - 3) and T(-4, 4) are plotten on the graph paper, then points in the fourth quadrant are :
(a) P and T
(b) Q and R
(c) S only
(d) P and R
Answer:
(b) Q and R

Question 5.
On plotting the points O(0, 0), A(3, 0), B(3, 4), C(0, 4) and joining OA, AB, BC and CO, which of the following figure is obtained?
(a) Square
(b) Rectangle
(c) Trapezium
(d) Rhombus
Answer:
(b) Rectangle

Question 6.
If P(5, 1), Q(8, 0), R(0, 4), 5(0, 5) and O(0, 0) are plotted on the graph paper, then point on X-axis are:
(a) P and R
(b) R and S
(c) only Q
(d) Q and O
Answer:
(d) Q and O

Question 7.
Abscissa is a point is positive in :
(a) I and II quadrants
(b) I and IV quadrants
(c) I quadrant only
(d) II quadrant only
Answer:
(b) I and IV quadrants

Question 8.
The point which lies on Y-axis at a distance of 5 units in the negative direction of Y-axis is:
(a) (0, 5)
(b) (5, 0)
(c) (0, -5)
(d) (- 5, 0)
Answer:
(c) (0, -5)

Question 9.
Abscissa of all the points on the X-axis is :
(a) 0
(b) 1
(c) 2
(d) any number
Answer:
(d) any number

Question 10.
If y-coordinate of the point is zero, then this point always lies :
(a) in I quadrant
(b) in II quadrant
(c) on X-axis
(d) on Y-axis
Answer:
(c) onX-axis

Question 11.
The distance of the point (4, 7) from Y-axis is :
(a) 4 units
(b) 7 units
(c) √65 units
(d) 11 units
Answer:
(a) 4 units

Question 12.
The point (-7, -5) lies in:
(a) first quadrant
(b) second quadrant
(c) third quadrant
(d) fourth quadrant
Answer:
(c) third quadrant

Question 13.
The coordinate of a point oh the x-axis is 3 units to the left of origin is:
(a) (0, 3)
(b) (3, 0)
(c) (0, -3)
(d) (-3, 0)
Answer:
(d) (-3, 0)

Question 14.
The point of intersection of the horizontal and vertical lines in the cartesian plane is called:
(a) zero point
(b) origin
(c) common point
(d) null point
Answer:
(b) origin

Question 15.
The distance of the point (- 5, 12) from y-axis is:
(a) - 5 units
(b) - 12 units
(c) 5 units
(d) 12 units
Answer:
(c) 5 units

II. Fill in the Blanks:
Whether the following statements are True or False.

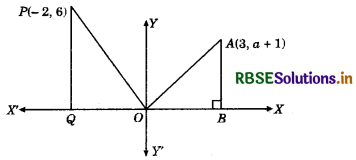
Question 1.
The point at which the two coordinate axes meet is called ____________ .
Answer:
the origin

Question 2.
Point (1, - 1) lies in ___________ quadrant.
Answer:
IV-quadrant

Question 3.
In the given figure area ∆OAB = area ∆OPQ then the ordinate of point A = ___________ .
Answer:
ordinate of point A = 4

Question 4.
Abscissa of a point is positive in ___________ .
Answer:
I and IV quadrants

Question 5.
Mirror image of point (3, 9) in X-axis is _________ .
Answer:
(3, -9)

III. True/False:
State whether the following statements are True or False.

Question 1.
Point (-4, -5) lies in the fourth quadrant.
Answer:
False

Question 2.
The perpendicular distance of the point (5, 6) from the x-axis is 5.
Answer:
False

Question 3.
Coordinates of a point on the x-axis are of the form (x, 0).
Answer:
True

Question 4.
Coordinates of a point on the y-axis are of the form (0, y).
Answer:
True

Question 5.
If y-coordinate of a point is zero, then this point always lies on y-axis.
Answer:
False

Question 6.
The perpendicular distance of the point A(4, 5) from x-axis is 5 units.
Answer:
True

Question 7.
The point (5, 0) lies on x-axis.
Answer:
True

IV. Match the Columns:
Match the column I with the column II.

Column I	Column II
(1) The point (-3, 0) lies on	(i) III quadrant
(2) The point (5, -6) lies on	(ii) II quadrant
(3) The point (-3, -6) lies on	(iii) x-axis
(4) The point (-3, 9) lies on	(iv) I quadrant
(5) The point (9, 7) lies on	(v) IV quadrant

Answer:

Column I	Column II
(1) The point (-3, 0) lies on	(iii) x-axis
(2) The point (5, -6) lies on	(v) IV quadrant
(3) The point (-3, -6) lies on	(i) III quadrant
(4) The point (-3, 9) lies on	(ii) II quadrant
(5) The point (9, 7) lies on	(iv) I quadrant

V. Very Short Answer Type Questions:

Question 1.
Find the coordinates of a point whose abscissa is - 3 and lies on x-axis.
Answer:
(- 3, 0).

Question 2.
In which quadrant can a point have abscissa equal to its ordinate?
Answer:
I and III quadrant.

Question 3.
What are the coordinates of a point that is the mirror image of point (0, 4) in X-axis?
Answer:
(0, - 4).

Question 4.
If x is positive and y is negative, then the point (x, y) lie in
Answer:
IV quadrant.

VI. Short Answer Type Questions:

Question 1.
A point lies on X-axis at a distance of 9 units from Y-axis. What are its coord in ates? JVVhat will be the coordinates of a point, if it lies on Y-axis at a distance of 9 units from X-axis in negative direction?
Answer:
We know that, coordinates of any point lies on X-axis at the distance ‘a’ from the Y-axis are (a, 0) and (- a, 0).
Since, the given point lies on X-axis at a distance of 9 units from Y-axis, so its coordinates are (9, 0) or (- 9, 0).
Now, if point lies on Y-axis at a distance of 9 emits from X-axis in negative direction, then its coordinates are (0, -9).

Question 2.
Plot the points P(1, 5), Q(3, 2), R(1, - 1) and S(- 1, 2) on a cartesian plane and join them in order. Now, write the name of the figure obtained.
Answer:
Let us draw mutually perpendicular axes XOX' and YOY' and choose a suitable units of distance on the axes. Let 1 cm = 1 unit. Then, the given points can be plotted as given below:

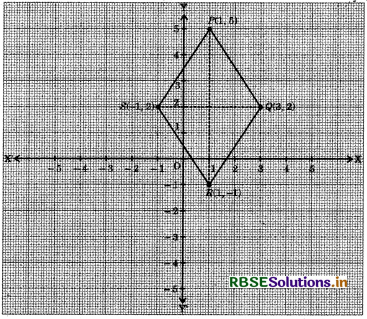
It is clear from the graph that all four sides are equal but diagonals are not equal, so it is a rhombus.

Question 3.
From the given figure, write:
(i) the coordinates of the points B and F.
(ii) the abscissa of points D and H.

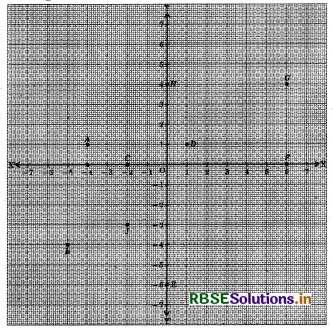
Answer:
(i) The coordinates of the points B and F are (-5, -4) and (6, 0) respectively.
(ii) The abscissa of points D and H are 1 and 0 respectively.

Question 4.
Plot the point P(2, - 6) on graph paper and from it draw PM and PN as perpendiculars to x-axis and y-axis respectively. Write the coordinates of the points M and N.
Answer:

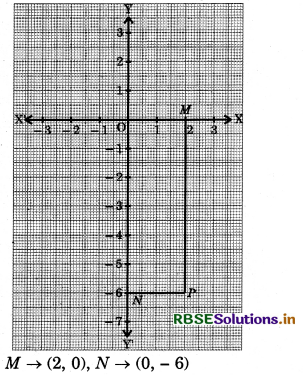
Question 5.
Three vertices of a square PQRS are P(- 4, 0), Q(1, 0), R(1, - 5). Plot the points. Also find the coordinates of the missing vertex S.
Answer:

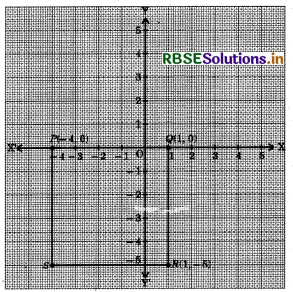
The coordinates of the missing vertex S are (- 4, - 5).

Question 6.
Plot two points P(1, 3) and Q(2, 6) on the graph sheet. Now, plot reflections of P and Q in X-axis and name them as S and R, respectively. Identify the figure PQRS.
Answer:
Let us we draw mutually perpendicular axes XOX' and YOY' and choose a suitable units of distance on the axes. Let 1 cm = 1 unit. Points P(1, 3) and Q(2, 6) have positive coordinates, so both points lies in I quadrant. The reflections of the point P and Q on X-axis are S(1, - 3) and R(2, - 6), respectively. Now, the points P, Q, R and S can be plotted as given below:

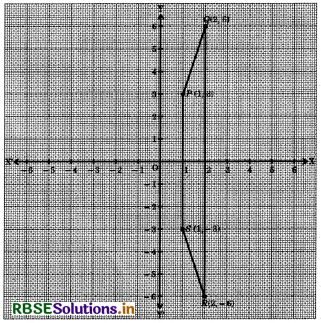
When we join all points adjacently, the figure PQRS formed a trapezium.

Question 7.
Write the coordinates of the vertices of a rectangle whose length and breadth are 4 units and 3 units respectively, has one vertex at the origin, the longer side is on the X-axis and one of the vertices lies in the IVth quadrant. Also find its area.
Answer:

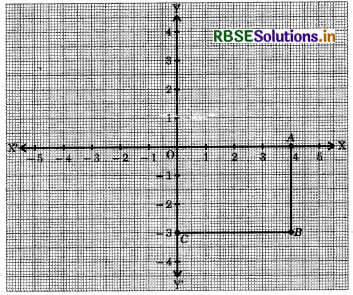
Area of the rectangle OABC = Length × Breadth
= 4 × 3 = 12 Square units

Question 8.
Plot the points (2, 3), (- 2, 3), (- 2, -3) and (2, - 3) on a graph sheet. Join these points. Name the figure obtained. Also, find the area of the figure so obtained.
Answer:

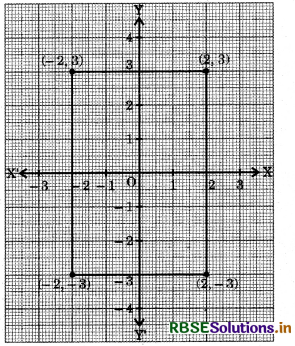
The figure obtained is a rectangle.
Area of the rectangle = 4 × 6 = 24 square units.

VII. Long Answer Type Questions:

Question 1.
In which quadrants do the given points lies?
(i) (4, - 2)
(ii) (- 3, 7)
(iii) (- 1, - 2)
(iv) (3, 6)
Answer:
(i) ∴ Points of the type (+, -) lies in IV quadrant.
∴ The point (4, - 2) lies in IV quadrant.

(ii) ∴ Points of the type (-, +) lies in II quadrant.
∴ The point (- 3, 7) lies in II quadrant.

(iii) ∴ Points of the type (-, -) lies in III quadrant.
∴ The point (-1,-2) lies in III quadrant.

(iv) ∴ Points of the type (+, +) lies in I quadrant.
∴ The point (3, 6) lies in I quadrant.

Question 2.
Draw a quadrilateral whose vertices are the points having coordinates as (- 5, 5), (5, 5), (5, - 5), (- 5, - 5). Write the special name of the quadrilateral so obtained. Also, find the area of the quadrilateral.
Answer:
Let us draw the coordinate axes XOX' and YOY'.
Let the points corresponding to the coordinates (- 5, 5), (5, 5), (5, - 5) and (- 5, - 5) be A, B, C and D respectively.
Now, let 1 unit = 1 cm. Then, the points A, B, C and D can be plotted as shown below:

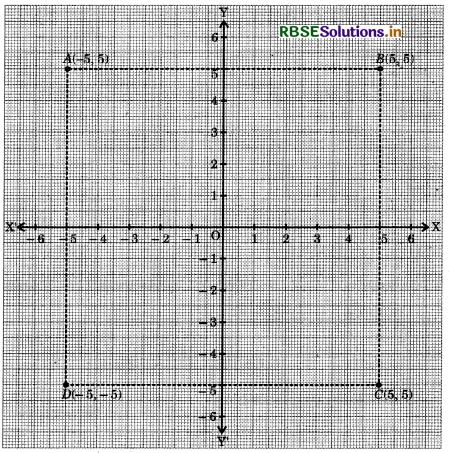
On joining A, B, C and D adjacently, we obtain a quadrilateral ABCD.
Here, all four sides are equal and diagonals are also equal.
∴The name of the quadrilateral, so obtained is the square ABCD.
Since, ABCD is a square and we know that, area of a square is equal to (Side)².
∴ Area of square ABCD = (Side)² = (10)² = 100 sq units Hence, the area of the quadrilateral is 100 sq units.

Question 3.
In figure, ∆ABC is an equilateral triangle with coordinates of B and C as B(1, 0) and C(5, 0). Find the coordinates of vertex A.

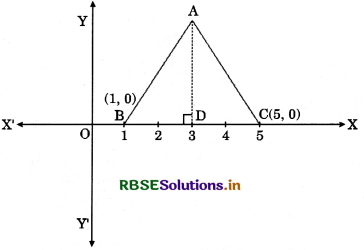
Answer:
Let D be the middle point of BC. Join AD.
Then, ∠BDA = 90°
∵AABC is an equilateral triangle.
∴AB = AC = BC
⇒ BC = 5 - 1 = 4 = AB
⇒ BD = 3 - 1 = 2
In right triangle BDA,
AB² = AD² + BD² (By Pythagoras Theorem)
⇒ (4)² = AD² + (2)²
⇒ 16 = AD² + 4
⇒ AD² = 12
⇒ AD = 2√3
∴ A → (3, 2√3)