RBSE Class 9 Maths Important Questions Chapter 2 Polynomials

Rajasthan Board RBSE Class 9 Maths Important Questions Chapter 2 Polynomials Important Questions and Answers.

RBSE Class 9 Maths Chapter 2 Important Questions Polynomials

I. Multiple Choice Questions:
Choose the correct answer from the given options.

Question 1.
The coefficient of x² in (3x² - 5) (4x + 4x²) is :
(a) 12
(b) 5
(c) - 8
(d) 8
Answer:
(c) - 8

Question 2.
Which of the following algebraic expression is a polynomial in one variable?
(a) 7x² - \(\frac{2}{x}\)
(b) 7x² - 3x + √2
(c) \(\frac{(x-2)(x-4)}{x}\)
(d) 7x² - xy + 5y + 2
Answer:
(b) 7x² - 3x + √2

Question 3.
Degree of the polynomial 4x⁴ + 0x³ + 0x⁵ + 5x + 7 is :
(a) 4
(b) 5
(c) 3
(d) 7
Answer:
(a) 4

Question 4.
If p(x) = x² - 2√2x +1, then p(2√2) is equal to :
(a) 0
(b) 1
(c) 4√2
(d) 8√2 + 1
Answer:
(b) 1

Question 5.
If a + b + c = 0, then the value of a³ + b³ + c³ is :
(a) 6
(b) abc
(c) 2abc
(d) 3abc
Answer:
(d) 3abc

Question 6.
The factorisation of 4a² + 8a + 3 is :
(a) (a + 1) (a + 3)
(b) (2a + 1) (2a + 3)
(c) (2a + 2) (2a + 5)
(d) (2a - 1) (2a - 3)
Answer:
(b) (2a + 1) (2a + 3)

Question 7.
If p(x) = x + 3, then p(x) + p(- x) is equal to :
(a) 3
(b) 2x
(c) 0
(d) 6
Answer:
(d) 6

Question 8.
The roots of the polynomial equation 3x³ - 12x = 0 are :
(a) 3, 2,-2
(b) 3, 0, 4
(c) 0, 2, -2
(d) 3, 0, 2, -2
Answer:
(c) 0, 2, -2

Question 9.
x + 1 is factor of the polynomial:
(a) x³ + x² - x + 1
(b) x³ + x² + x + 1
(c) x⁴ + x³ + x² + 1
(d) x⁴ + 3x³ + 3x² + x + 1
Answer:
(b) x³ + x² + x + 1

Question 10.
The value of the polynomial 5x - 4x² + 3, then x = - 1 is
(a) - 6
(b) 6
(c) 2
(d) - 2
Answer:
(a) - 6

Question 11.
If 49x² - b = (7x + \(\frac{1}{2}\))(7x - \(\frac{1}{2}\)) , then the value of b is :
(a) 0
(b) \(\frac{1}{\sqrt{2}}\)
(c) \(\frac{1}{4}\)
(d) \(\frac{1}{2}\)
Answer:
(c) \(\frac{1}{4}\)

Question 12.
If \(\frac{x}{y}+\frac{y}{x}\) = -1 (x, y ≠ 0), then the value of x³ - y³ is :
(a) 1
(b) -1
(c) 0
(d) \(\frac{1}{2}\)
Answer:
(c) 0

Question 13.
The coefficient of x in the expansion of (x + 3)³ is :
(a) 1
(b) 9
(c) 18
(d) 27
Answer:
(d) 27

Question 14.
The factors of x² - √2x - 4 are ;
(a) (x + 2√2)(x + √2)
(b) (x - 2√2)(x - √2)
(c) (x - 2√2) (x + √2)
(d) (x + 2)(x - 2√2)
Answer:
(c) (x - 2√2) (x + √2)

Question 15.
If x² + kx + 6 = (x + 2)(x + 3) for all x, then the value of k is :
(a) 1
(b) -1
(c) 5
(d) 3
Answer:
(c) 5

II. Fill in the Blanks :

Question 1.
The coefficient of x² in the polynomial (x - 1) (- 3x - 4) is ____________
Answer:
3

Question 2.
Degree of polynomial 4 - y² is ____________
Answer:
2

Question 3.
If - 1 is a zero of the polynomial, x² + 8x + k, then the value of k =
Answer:
k = 7

Question 4.
If 3x - 1 is a factor of the polynomial 6x² + x - 1, then its other factor is
Answer:
2x + 1

Question 5.
If (x + 1) and (x + 2) are factors of x³ + 3x² - 2αx + β, then α = ____________ and β = ____________
Answer:
-1, 0

Question 6.
If a + b + c = 9 and ab + bc + ca = 26, then a² + b² + c² =
Answer:
29

III. True/False:
State whether the following statements are True or False.

Question 1.
If (x - 1) is a factor of polynomial 4x³ + 3x² - 4x + k, then the value of k is 3.
Answer:
False

Question 2.
A binomial can have at most two terms.
Answer:
False

Question 3.
Every polynomial is binomial.
Answer:
False

Question 4.
A binomial may have degree 5.
Answer:
True

Question 5.
Zero of a polynomial is also the factor of given polynomial.
Answer:
True

Question 6.
A polynomial cannot have more than one zero.
Answer:
False

Question 7.
The degree of the sum of two polynomials each of degree 5 is always 5.
Answer:
False

IV. Match the Columns

Question 1.
Match the column I with the column II.

Column I	Column II
(1) Zero of zero polynomial is	(i) -3
(2) Degree of the zero polynomial is	(ii) 3
(3) Coefficient of y2 in the expression (y - l)3 is	(iii) not defined
(4) If x101 + 4 is divided by x + 1, the reminder is	(iv) -6
(5) If p(x) = 7x2 - 4 √2 is completely divisible by (x - √2), then c =	(v) any real number

Answer:

Column I	Column II
(1) Zero of zero polynomial is	(v) any real number
(2) Degree of the zero polynomial is	(iii) not defined
(3) Coefficient of y2 in the expression (y - 1)3 is	(i) -3
(4) If x101 + 4 is divided by x + 1, the reminder is	(ii) 3
(5) If p(x) = 7x2 - 4 √2 is completely divisible by (x - √2), then c =	(iv) -6

V. Very Short Answer Type Questions :

Question 1.
Find k, if x⁵¹ + 2x⁶⁰ + 3x + k is divisible by x + 1.
Answer:
Let p(x) = x⁵¹ + 2x⁶⁰ + 3x + k
Given that, p(x) is divisible by x + 1.
∴ p(-1) = 0
⇒ (- 1)⁵¹ + 2(- 1)⁶⁰ + 3(- 1) + k = 0
⇒ -1 + 2 - 3 + k = 0
⇒ k - 4 + 2 = 0
⇒ k - 2 = 0
⇒ k = 2

Question 2.
Give possible expression for the length and breadth of the rectangle, whose area is given by 4a² + 4a - 3.
Answer:
Given, area of rectangle = 4a² + 4a - 3
= 4a² + 6a - 2a - 3 [By splitting the middle term]
= 2a (2a + 3) - 1 (2a + 3)
= (2a - 1) (2a + 3)
Hence, possible expression for length/breadth = (2a - 1) and possible expression for breadth/length = (2a + 3).

Question 3.
What are the possible expressions for the dimensions of a cuboid, whose volume is 36fex2y - 21 kxy2 + 3fey3?
Answer:
Volume = 36kx²y - 21 kxy² + 3ky³
= 3ky(12x² - 7xy + y²)
= 3ky(12x² - 4xy — 3xy + y2)
= 3ky[4x(3x - y) - y(3x - y)]
= 3ky(4x - y)(3x - y)
Hence, possible expression for length/breadth/height = Sky, possible expression for breadth/height/length = 4x - y and possible expression for height/length/breadth = 3x - y.

Question 4.
Expand (x - \(\frac{1}{2}\)y + \(\frac{1}{3}\)z)²
Answer:
 (x - \(\frac{1}{2}\)y + \(\frac{1}{3}\)z)² = (x)² + (- \(\frac{1}{2}\)y)² + (\(\frac{1}{3}\)z)² + 2x(- \(\frac{1}{2}\)y) + 2(- \(\frac{1}{2}\)y)(\(\frac{1}{3}\)z) + 2(\(\frac{1}{3}\)z)(x)
[∵ (a + b + c)² = a² + b² +c² +2ab +2bc + 2ca]
= x² + \(\frac{1}{4}\)y² + \(\frac{1}{9}\)z² - xy - \(\frac{y z}{3}+\frac{2 z x}{3}\)

Question 5.
Without calculating the cubes find the value of (- 11)³ + (8)³ + (3)³.
Answer:
We have,
(-11) + 8 + 3 = 0
Therefore, (- 11)³ + (8)³ + (3)³ = 3(- 11) (8) (3) = - 792
(∵ If x + y + z = 0, then x³ + y³ + z³ = 3xyz)

VI. Short Answer Type Questions :

Question 1.
If x + 2y = 10, xy = 15, then find x³ + 8y³.
Answer:
We know that
(x + 2y)³ = (x)³ + (2y)³ + 3(x)(2y) (x + 2y) (Using Identity VI)
⇒ (x + 2y)³ = x³ + 8y³ + 6xy(x + 2y)
⇒ (10)³ = x³ + 8y³ + 6(15)(10)
⇒ 1000 = x³ + 8y³ + 900
⇒ x³ + 8y³ = 1000 - 900 = 100

Question 2.
Factorise : a⁷ + ab⁶.
Answer:
a⁷ + ab⁶ = a(a⁶ + b⁶) = a{(a²)³ + (b²)³}
= a(a² + b²) {(a²)² + (b²)² - (a²) (b²)}
= a(a² + b²) (a⁴ + b⁴ - a²b²)
= a(a² + b²) (a⁴ + b⁴ + 2a²b² - 2a²b² - a²b²)
= a(a² + b²) (a⁴ + b⁴ + 2a²b² - 3a²b²)
= a(a² + b²) {(a² + b²)² - (√3 ab)²}
= a(a² + b²) (a² + b² - √3 3ab) (a² + b² + √3 ab).

Question 3.
If p(x) = x² - 4x + 3, then evaluate p(2) - p(- 1) + p(1/2).
Answer:
p(2) = (2)² - 4(2) + 3 = 4 - 8 + 3 = -1
p(- 1) = (- 1)² - 4(- 1) + 3 = 1 + 4 + 3 = 8
p\(\left(\frac{1}{2}\right)\) = \(\left(\frac{1}{2}\right)^{2}\) - 4\(\left(\frac{1}{2}\right)\) + 3 = \(\frac{1}{4}\) - 2 + 3 = \(\frac{5}{4}\)
∴ p(2) - p(-1) + p\(\left(\frac{1}{2}\right)\) = -1 - 8 + \(\frac{5}{4}=\frac{-31}{4}\)

Question 4.
Use Factor Theorem to verify that x + a is a factor of xⁿ + aⁿ for any odd positive integer n.
Answer:
Let p(x) = xⁿ + aⁿ
The zero of x + a is - a. (x + a = 0 ⇒ x = - a)
Now, p(- a) = (- a)ⁿ + aⁿ = (- 1 )ⁿaⁿ + aⁿ
[∵ n is an odd positive integer]
[∴ (-1)ⁿ = -1]
= (-1)aⁿ + aⁿ = 0
= - aⁿ + aⁿ = 0
∴ By Factor Theorem, x + a is a factor of xn + an for any odd positive integer n.

The remainder of the polynomial 5 + bx - 2x² + ax³, when divided by (x - 2) is twice the remainder when it is divided by (x + 1). Show that 10a + 46 = 9.
Answer:
Let f(x) = 5 + bx - 2x² + ax³
When f(x) is divided by (x - 2), then the remainder is f(2).
When f(x) is divided by (x + 1), then the remainder is f(-1).
Now, f(2) = 5 + 6(2) - 2(2)² + a(2)³ = 8a + 2b - 3
and f(-1) = 5 + 6(- 1) - 2(- 1)² + a(- 1)³ = - a - b + 3

According to the question, f(2) = 2f(- 1)
∴ 8a + 2b - 3 = 2 (- a - 6 + 3)
⇒ 8a + 2b - 3 = -2a - 2b + 6
⇒ 10a + 4b = 9
Hence proved.

Question 6.
Show by long division that (x - 3) is a factor of 2x⁴ + 3x³ - 26x² - 5x + 6.
Answer:
We have to show that remainder is zero, while divide 2x⁴ + 3x³ - 26x² - 5x + 6 by (x - 3).

Hence, (x - 3) is a factor of 2x⁴ + 3x³ - 26x² - 5x + 6.

Question 7.
The polynomial 3x³ + ax² + 3x + 5 and 4x³ + x² - 2x + a leave remainder and R2, when divided by (x - 2) respectively. If R₁ - R₂ = 9, then find the value of a.
Answer:
Let f(x) = 3x³ + ax² + 3x + 5 and g(x) = 4x³ + x² - 2x + a Here, the zero of (x - 2) is x = 2. (∵ x - 2 = 0 ⇒ x = 2)

Where f(x) and g(x) are divided by (x - 2), then we get the remainders R₁ and R₂.
f(2) = 3(2 )³ + a(2)³ + 3(2) + 5
= 24 + 4a + 6 + 5
= 35 + 4a = R₁ (Given)
and g(2) = 4(2)³ + (2)² - 2(2) + a
= 32 + 4- 4 + a
= 32 + a = R₁ (Given)
Also, R₁ - R₂ - 9
∴ 35 + 4a - (32 + a) = 9
⇒ 3 + 3a = 9
⇒ 3a = 6 ⇒ a = 3

VII. Long Answer Type Questions :

Question 1.
If both (x - 2) and (x - \(\frac{1}{2}\)) are factors of px² + 5x + r, then show that p = r.
Answer:
Let f(x) = px² + 5x + r
If (x - 2) is a factor of fix), then by factor theorem.
f(2) = 0 (x - 2 = 0)
⇒ x = 2
⇒ p(2)² + 5(2) + r = 0
⇒ 4p + r + 10 = 0 ...................(1)

If (x - \(\frac{1}{2}\)) is a factor of f(x), then by factor theorem,
f(\(\frac{1}{2}\)) = 0 (x - \(\frac{1}{2}\) = 0 ⇒ x = \(\frac{1}{2}\))
⇒ p\(\left(\frac{1}{2}\right)^{2}\) + 5(\(\frac{1}{2}\)) + r = 0
⇒ \(\frac{p}{4}+\frac{5}{2}\) + r = 0
⇒ p + 4r + 10 = 0 ......(2)

Subtracting (2) from (1), we get : .
3p - 3r = 0
⇒ p = r
Hance proved.

Question 2.
Divide the polynomial 3x⁴ - 4x³ - 3x - 1 by x - 1 and find its quotient and remainder.
Answer:

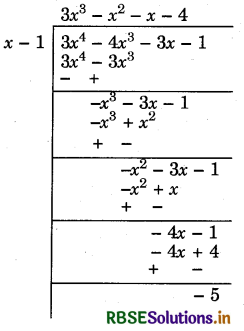
Quotient = 3x³ - x² - x - 4
and Remainder = - 5

Question 3.
If x + a is a factor of the polynomials x² + px + q and x² + mx + n, prove that
a = \(\frac{n-q}{m-p}\)
Answer:
Let f(x) = x² + px + q
and g(x) = x² + mx + n
If x + a is a factor of f(x), then by factor theorem
f(a) = 0 (x + a = 0 ⇒ x = -a)
⇒ (- a)² + p(- a) + q = 0
⇒ a² - pa + q = 0 ........(1)

If x + a is a factor of g(x), then by factor theorem
g(- a) = 0 (x + a = 0 ⇒ x = -a)
⇒ (- a)² + m(- a) + n - 0
a² - ma + n = 0 ............(2)

Subtracting (1) from (2), we get :
(p - m)a + (n - q) = 0
⇒ (m - p)a = n - q
⇒ a = \(\frac{n-q}{m-p}\)
Hence Proved.