RBSE Class 9 Maths Important Questions Chapter 2 बहुपद

Rajasthan Board RBSE Class 9 Maths Important Questions Chapter 2 बहुपद Important Questions and Answers.

RBSE Class 9 Maths Chapter 2 Important Questions बहुपद

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
बहुपद p (x) का शून्यक, जहाँ p (x) = ax + 1 है, a ≠ 0 है-
(A) 1
(B) - a
(C) 0
(D) -\(\frac{1}{a}\)
उत्तरः
(D) -\(\frac{1}{a}\)

प्रश्न 2.
3x² - x - 4 के गुणनखण्ड हैं
(A) (x - 1) तथा (3x - 4)
(B) (x + 1) तथा (3x - 4)
(C) (x + 1) तथा (3x + 4)
(D) (x - 1) तथा (3x + 4)
उत्तरः
(B) (x + 1) तथा (3x - 4)

प्रश्न 3.
बहुपद 3y - y² + 4 की घात है
(A) 2
(B) 1
(C) 3
(D) 4
उत्तरः
(A) 2

प्रश्न 4.
यदि (x + 1) बहुपद 2x³ + 8x² + 3x + k का एक गुणनखण्ड है तब k का मान है-
(A) 3
(B) 4
(C) 5
(D) - 3
उत्तरः
(D) - 3

प्रश्न 5.
a के किस मान के लिए (x - 3) बहुपद x³ + x² - 17x+ a का गुणनखण्ड है
(A) 18
(B) 12
(C) 15
(D) - 5
उत्तरः
(C) 15

प्रश्न 6.
बहुपद 6 - x² + 8x की घात है-
(A) 3
(B) - 1
(C) 2
(D) 1
उत्तरः
(C) 2

प्रश्न 7.
(998)² + (994)² - 1996 × 994 बराबर है
(A) 16
(B) 4
(C) 20
(D) 24
उत्तरः
(A) 16

प्रश्न 8.
यदि (x - 2) बहुपद x² + 3ax - 2a का एक गुणनखण्ड हो, तो a का मान होगा
(A) - 1
(B) 1
(C) - 2
(D) 2
उत्तरः
(A) - 1

प्रश्न 9.
यदि किसी बहुपद x + x² - 20 का एक गुणनखण्ड x² + 5 है तो दूसरा गुणनखण्ड होगा-
(A) x² - 4
(B) x² - 5
(C) x - 4
(D) x + 2
उत्तरः
(A) x² - 4

प्रश्न 10.
यदि 51 + 51, (x + 1) से भाज्य है तो शेषफल होगा-
(A) 0
(B) 1
(C) 50
(D) 49
उत्तरः
(C) 50

रिक्त स्थानों की पूर्ति करो

प्रश्न 1.
वह समीकरण जो चर राशियों के सभी मानों के लिए सत्य हो, ............................ कहलाती है।
उत्तर:
सर्वसमिका

प्रश्न 2.
बहुपद p(x) = 4x² - 25 के शून्यक .............................. और
उत्तर:
\(\frac{5}{2},-\frac{5}{2}\)

प्रश्न 3.
यदि \(\frac{x}{y}+\frac{y}{x}\) = - 1(x, y ≠ 0) तब x³ - y³ का मान ..................... है।
उत्तर:
0

प्रश्न 4.
यदि \(a^{1 / 3}+b^{1 / 3}+c^{1 / 3}\) = 0 है तब (a + b + c)³
उत्तर:
27abc

प्रश्न 5.
यदि (x + y)³ - (x - y)³ - 6y(x² - y²) = ky², तब k = ..........................
उत्तर:
8

प्रश्न 6.
यदि p(x), एक से अधिक या एक के बराबर घात वाला एक बहुपद हो, और p(x) को रैखिक बहुपद ...................... से भाग दिया गया हो, तो शेषफल p(a) होता है।
उत्तर:
x - a

प्रश्न 7.
यदि p(a) = 0, हो तो x - a, p(x) का एक .................... होता है।
उत्तर:
गुणनखण्ड

प्रश्न 8.
यदि x¹⁴⁰ + 2x¹⁵¹ + k, x + 1 से विभाज्य है, तब k का मान .............................. है।
उत्तर:
1

सत्य/असत्य-निम्नलिखित कथनों के लिए सत्य अथवा असत्य लिखिए

प्रश्न 1.
√5 शून्य घात का एक बहुपद है।
उत्तर:
सत्य

प्रश्न 2.
प्रत्येक वास्तविक संख्या शून्य बहुपद की शून्यक होती है।
उत्तर:
सत्य

प्रश्न 3.
प्रत्येक बहुपद द्विपदीय होता है।
उत्तर:
असत्य

प्रश्न 4.
किसी भी बहुपद के एक से ज्यादा शून्यक नहीं हो सकते।
उत्तर:
असत्य

प्रश्न 5.
यदि (x - 1), बहुपद 4x³ + 3x² - 4x + k का एकं गुणनखण्ड है, तब k का मान 3 है।
उत्तर:
असत्य

प्रश्न 6.
यदि x² - 1, ax⁴ + bx³ + cx² + dx + e का एक गुणनखण्ड है, तब a + c + e = b + d. होगा।
उत्तर:
सत्य

प्रश्न 7.
यह आवश्यक नहीं है कि बहुपद का शून्यक शून्य ही हो।
उत्तर:
असत्य

प्रश्न 8.
यदि (x + a), x⁴ - a²x² + 3x - 6a का एक गुणनखण्ड है, तब a का मान - 1 होगा।
उत्तर:
असत्य

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
उपयुक्त सर्वसमिका का प्रयोग करते हुए गुणनफल \(\left(a-\frac{1}{a}\right)\left(a+\frac{1}{a}\right)\left(a^{2}+\frac{1}{a^{2}}\right)\left(a^{4}+\frac{1}{a^{4}}\right)\) ज्ञात कीजिए।
हल:
\(\left(a-\frac{1}{a}\right)\left(a+\frac{1}{a}\right)\left(a^{2}+\frac{1}{a^{2}}\right)\left(a^{4}+\frac{1}{a^{4}}\right)\)
= \(\left(a^{2}-\frac{1}{a^{2}}\right)\left(a^{2}+\frac{1}{a^{2}}\right)\left(a^{4}+\frac{1}{a^{4}}\right)\)
[सर्वसमिका (a - b) (a + b) = a² - b² के अनुसार]
= \(\left(a^{4}-\frac{1}{a^{4}}\right)\left(a^{4}+\frac{1}{a^{4}}\right)=\left(a^{4}\right)^{2}-\left(\frac{1}{a^{4}}\right)^{2}\)
= \(a^{8}-\frac{1}{a^{8}}\)

प्रश्न 2.
गुणनखण्ड कीजिए- x² - y² + 2x + 1
हल:
x² - y² + 2x + 1
= x² + 2x + 1 - y²
= (x + 1)² - y²
= (x + 1 - y) (x + 1 + y)
= (x - y + 1) (x + y + 1)

प्रश्न 3.
(3x + 2y) (3x - 2y) (9x2 + 4y) का गुणनफल ज्ञात कीजिए।
हल:
(3x + 2y) (3x - 2y) (9x + 4y)
= {(3x)² - (2y)²} (9x² + 4y²)
= (9x² - 4y²) (9x² + 4y²)
= (9x²)² - (4y²)²
= 81x⁴ - 16y⁴

प्रश्न 4.
k के किस मान के लिए x³ + 2x² + 5x + k का एक गुणनखण्ड (x + 1) है?
हल:
यदि (x + 1) दिए गए बहुपद का एक गुणनखण्ड है तो x + 1 = 0 ⇒ x = - 1 से बहुपद का मान शून्य होना चाहिए।
x³ + 2x² + 5x + k = 0
(-1)³ + 2(- 1)² + 5 (- 1) + k= 0
- 1 + 2 - 5 + k = 0
- 4 + k = 0
k = 4

प्रश्न 5.
यदि (x - 3) बहुपद व्यंजक p (x) = x³ - 3x² + 4x - 12 का एक गुणनखण्ड है तो p (3) का मान लिखिए।
हल:
x - 3 = 0 या x = 3 व्यंजक p (x) में रखने पर
p (3) = (3)³ - 3 (3)² + 4 (3) – 12
= 27 - 3 × 9+ 12 - 12
= 27 - 27 + 12 - 12
= 0

प्रश्न 6.
यदि a + b = - c हो तो a³ + b³ + 3ab (a + b) का मान c के पदों में लिखिए।
हल:
प्रश्नानुसार (a + b)³ = a³ + b³ + 3ab (a + b)
∴ दिया गया प्रश्न = (a + b)³
= (-c)³ = –c³

प्रश्न 7.
बहुपद \(\left(z+\frac{3}{4}\right)\left(z+\frac{4}{3}\right)\) का मानक रूप लिखते हुए इसकी घात भी लिखिए।
हल:

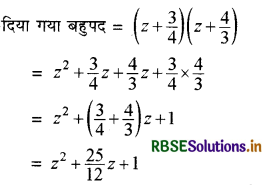
यही इसका मानक रूप है तथा इस बहुपद की घात = 2

प्रश्न 8.
सत्यापित कीजिए कि 2 और 0 बहुपद x² - 2x के शून्यक हैं।
हल:
माना कि p (x) = x² - 2x
तब p (2) = 2² - 2 (2) = 4 - 4 = 0
तथा p (0) = 0 - 0 = 0
अतः 2 और 0 दोनों ही बहुपद x² - 2x के शून्यक हैं।

प्रश्न 9.
बहुपद x⁴ + x³ - 2x² + x + 1 को x-1 से भाग देने पर प्राप्त शेषफल ज्ञात कीजिए।
हल:
प्रश्नानुसार बहुपद p (x) = x⁴ + x³ - 2x² + x + 1 है तथा x – 1 का शून्यक 1 है।
∴p (1) = (1)⁴ + (1)³ - 2 (1) + 1 + 1
= 1 + 1 - 2 + 1 + 1 = 2
अतः शेषफल प्रमेय के अनुसार x⁴ + x³ - 2x² + x + 1 को (x - 1) से भाग देने पर शेषफल 2 प्राप्त होता

प्रश्न 10.
यदि (x - 1), 4x³ + 3x² - 4x + k का एक गुणनखण्ड है, तो k का मान ज्ञात कीजिए।
हल:
क्योंकि प्रश्नानुसार (x - 1), p (x) = 4x³ + 3x² - 4x + k का एक गुणनखण्ड है इसलिए p (1) = 0 होगा।
अत: p (1) = 4(1)³ + 3(1)² - 4(1) + k
∴ 4 + 3 - 4 + k = 0
या k = - 3

प्रश्न 11.
(4a - 2b - 3c) का प्रसार कीजिए।
हल:
(4a - 2b - 3c)²
सर्वसमिका (x + y + z)² = x² + y² + z² + 2xy + 2yz + 2x के अनुसार
= [4a + (- 2b) + (-3c)]²
= (4a)² + (- 2b)² + (-3c)² + 2 (4a) (- 2b) + 2 (- 2b) (-3c) + 2 (- 3c) (4a)
= 16a² + 4b² + 9c² - 16ab + 12bc - 24ac

प्रश्न 12.
8x² + y³ + 27z³ - 18xyz का गुणनखण्ड कीजिए।
हल:
प्रश्नानुसार 8x³ + y² + 27z³ - 18xyz
= (2x)³ + y³ + (37)² - 3 (2x) (y) (32)
= (2x + y + 3z) [(2x) + y + (32) - (2x) (y) - (y) (37) - (2x) (32)]
= (2x + y + 37) (4x² + y² + 9z² - 2xy - 3yz - 6xz)

प्रश्न 13.
उपयुक्त सर्वसमिका का प्रयोग करते हुए बहुपद 16x² + 24xy + 9y² का गुणनखण्ड कीजिए।
हल:
16x² + 24xy + 9y²
[सर्वसमिका (a + b)² = a² + 2ab + b² का प्रयोग करने पर
= (4x)² + 2 . (4x) (3y) + (3y)²
= (4x + 3y)²

प्रश्न 14.
यदि बहुपद f (x) = 2x⁴ - 6x³ + 2x² - x + 2, (x + 2) से भाज्य हो तो शेषफल ज्ञात कीजिए।
हल:
∵ x + 2 = x - (-2)
शेषफल प्रमेय के अनुसार यदि f (x), (x + 2) = {x - (-2)} से भाज्य हो तो शेषफल f (-2) के बराबर होगा।
अर्थात् f (x) = 2x⁴ - 6x³ + 2x² - x + 2
∴ f (- 2) = 2 (-2)⁴ - 6 (-2)³ + 2 (-2)² - (-2) + 2
= 2 × 16 - 6 × - 8 + 2 × 4 + 2 + 2
= 32 + 48 + 8 +4
= 92
∴ शेषफल = 92

प्रश्न 15.
प्रदर्शित कीजिए कि बहुपद x¹⁰ - 1 और x11 - 1 का एक गुणनखण्ड (x - 1) है।
हल:
माना कि p (x) = x¹⁰ - 1
तथा q (x) = x¹¹ - 1
यह प्रदर्शित करने के लिए कि (x - 1), बहुपद p (x) तथा q (x) का एक गुणनखण्ड है, यह दिखाना पड़ेगा कि p (1) = 0 तथा q (1) = 0
∴ p (x) = x¹⁰ - 1 तथा q(x) = x¹¹ - 1
⇒ p (1) = 1¹⁰ - 1 तथा q (1) = 1¹¹ - 1
⇒ p (1) = 0 तथा q(1) = 0
अत: यह कहा जा सकता है कि p (x) तथा q (x) बहुपद का (x - 1) एक गुणनखण्ड है।

लघूत्तरात्मक प्रश्न

प्रश्न 1.
सरल कीजिए(x² + y² - z²)² - (x² - y² + z²)²
हल:
प्रश्नानुसार

प्रश्न 2.
यदि \(\left(x+\frac{1}{x}\right)\) = 9 है तो \(x^{3}+\frac{1}{x^{3}}\) का मान ज्ञात कीजिए।
हल:
सर्वसमिका

प्रश्न 3.
8x³ + 27y³ का मान ज्ञात कीजिए, यदि 2x + 3y = 18 तथा xy = 12.
हल:
प्रश्नानुसार 2x + 3y = 18 तथा xy = 12
अब (2x + 3y)³ = (2x)³ + (3y)³ + 3 (2x) (3y) (2x + 3y)
= 8x³ + 27y³ + 18 (2x + 3y)
[सर्वसमिका (a + b)³ = a³ + b³ + 3ab (a + b) के अनुसार]
⇒ 8x³ + 27y³ = (2x + 3y)³ - 18y (2x + 3y)
= (18)³ - 18 × 12 × 18
= 5832 - 3888
= 1944

प्रश्न 4.
बहुपदp (x) = x³ + 1 को x + 1 से भाग देने पर प्राप्त शेषफल ज्ञात कीजिए।
हल:

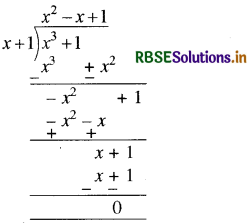
अर्थात् उपर्युक्त में शेषफल 0 है।

प्रश्न 5.
जाँच कीजिए कि बहुपद q (t) = 4t³ + 4t² - t - 1, 2t + 1 का एक गुणज है।
हल:
आप जानते हैं कि (1) बहुपद 2t + 1 का गुणज केवल तब होगा जबकि 2t + 1 से q(t) को भाग देने पर कोई भी संख्या शेष न बचे। अब 2t + 1 = 0

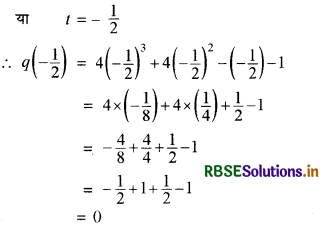
अतः q (t) को 2t + 1 से भाग देने पर प्राप्त शेषफल = 0
अत: 2t + 1 दिए हुए बहुपद q (t) का एक गुणनखण्ड है अर्थात् q (t), 2t + 1 का एक गुणज है।

प्रश्न 6.
शेषफल ज्ञात कीजिए यदि बहुपद 4x³ - 3x² + 2x -4 को (x + \(\frac{1}{2}\)) से भाग दिया जाए।
हल:
प्रश्नानुसार x + \(\frac{1}{2}\) = 0 ⇒ x = - \(\frac{1}{2}\) दिए गए बहुपद में प्रतिस्थापित करने पर
अर्थात् माना

प्रश्न 7.
(\(\frac{1}{4}\)a - \(\frac{1}{2}\)b + 16)² का प्रसार कीजिए।
हल:
प्रश्नानुसार (\(\frac{1}{4}\)a - \(\frac{1}{2}\)b + 16)²
सर्वसमिका (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca के अनुसार \(\left[\frac{1}{4} a+\left(-\frac{1}{2} b\right)+16\right]\)

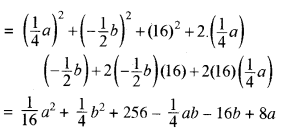
प्रश्न 8.
यदि 2x - 3 = a हो, तो सिद्ध कीजिए कि 8x³ - 18ax = a³ + 27.
हल:
प्रश्नानुसार 2x - 3 = a
दोनों पक्षों का घन करने पर
(2x - 3)³ = (a)³
या (2x)³ - (3)³ - 3 (2x) (3) (2x – 3) = a³
[∵ सर्वसमिका (a - b)³ = a³ - b³ - 3ab (a - b) के अनुसार]
या 8x³ - 27 - 18 (x) (a) = a³
∵ 2x - 3 = a
अतः 8x³ - 18ax = a³ + 27 (इतिसिद्धम्)

प्रश्न 9.
यदि y = \(\frac{4}{3}\) एक बहुपदीय व्यंजक f(y) = 6y³ - 11y² + ky - 20 का एक मूल है तो k का मान ज्ञात कीजिए।
हल:
प्रश्नानुसार f (y) = 6y³ - 11y² + ky - 20

प्रश्न 10.
यदि बहुपद f (x) = x³ - 6x² + 2x - 4, g (x) = 3x - 1 से भाज्य है तो शेषफल ज्ञात कीजिए।
हल:
प्रश्नानुसार g (x) = 3x - 1 = 3\(\left(x-\frac{1}{3}\right)\)
∴ शेषफल प्रमेय के अनुसार f (x), g(x) = 3\(\left(x-\frac{1}{3}\right)\) द्वारा भाज्य होगा यदि शेषफल f\(\left(\frac{1}{3}\right)\) के बराबर हो।
अत: f (x) = x³ - 6x² + 2x - 4

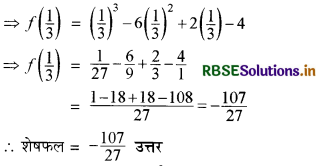
प्रश्न 11.
यदि बहुपद 2x⁴ - ax³ + 4x² + 2x + 1, (1 - 2x) द्वारा भाज्य है तो a का मान ज्ञात कीजिए।
हल:
माना कि p (x) = 2x⁴ - ax³ + 4x² + 2x + 1
यदि यह बहुपद p (x), पद (1 - 2x) द्वारा भाज्य है तो (1 - 2x), p (x) का एक गुणनखण्ड होगा।

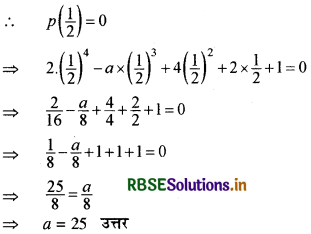
प्रश्न 12.
यदि पद (x² - 1) बहुपद ax⁴ + bx³ + cx² + dx +e का एक गुणनखण्ड है तो प्रदर्शित करो कि a + c + e = b + d = 0
हल:
माना कि
p (x) = ax⁴ + bx³ + cx² + dx + e
तब (x² - 1) इसका एक गुणनखण्ड है।
या (x - 1) (x + 1) इसका एक गुणनखण्ड है।
अर्थात् (x - 1) तथा (x + 1) बहुपद p (x) के गुणनखण्ड हैं।
या p (1) = 0 तथा p (- 1) = 0
[∵ x - 1 = 0 ⇒ x = 1
तथा x + 1 = 0 ⇒ x = - 1]
⇒ a + b + c + d + e = 0
तथा a - b + c - d + e = 0
इन दोनों समीकरणों को जोड़ने व घटाने पर
2(a + c + e) = 0 तथा 2 (b + d) = 0
या a + c + e = 0 तथा b + d = 0
⇒ a + c + e = b + d = 0 (इतिसिद्धम)

प्रश्न 13.
बहुपद व्यंजक x⁶ - 7x³ - 8 का गुणनखण्ड कीजिए।
हल:
प्रश्नानुसार x⁶ - 7x - 8
माना कि y = x³
अर्थात् (x³)² - 7(x³) - 8
या y² - 7y - 8
= y² - 8y + y - 8
= y (y - 8) + 1(y - 8)
= (y - 8) (y + 1)
y का मान रखने पर (x³ - 8) (x³ + 1)
= (x³ - 2³) (x³ + 1³)
= (x - 2) (x² + 2x + 4) (x + 1) (x² - x + 1)
= (x - 2) (x + 1) (x² + 2x + 4) (x² - x + 1)

निबन्धात्मक प्रश्न

प्रश्न 1.
गुणनखण्ड कीजिए- x³ - 2x² - 5x + 6.
हल:
माना कि p (x) = x³ - 2x² - 5x + 6 अब हम 6 के समस्त गुणनखण्ड लिखेंगे-
± 1, ± 2, ± 3
दिए गए बहुपद में x = 1 रखने पर
p (1) = (1)³ - 2 (1)² - 5(1) + 6
= 1 - 2 - 5 + 6
= - 7 + 7 = 0
अर्थात् दिए गए बहुपद का (x - 1) एक गुणनखण्ड है।

अतः x³ - 2x² - 5x + 6
= (x - 1) (x² - x - 6)
= (x - 1) [x³ - 3x + 2x - 6]
= (x - 1) [x (x - 3) + 2 (x - 3)]
= (x - 1) (x - 3) (x + 2)
= (x - 1) (x + 2) (x - 3)

प्रश्न 2.
गुणनखण्ड कीजिए
8x³ - \(\frac{1}{27}\) + 125y³ + 10xy
हल:

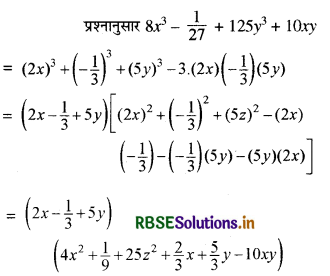
प्रश्न 3.
गुणनखण्ड कीजिए-
a³(b - c)³ + b³ (c - a)³ + c³ (a - b)³.
हल:
प्रश्नानुसार a³ (b - c)³ + b³ (c - a)³ + c³ (a - b)³
= {a(b - c)}³ + {b (c - a)}³ + {c (a - b)}³
अब माना कि a (b - c) = x, b (c - a) = y तथा c (a - b) = z
तब x + y + z = a (b - c) + b (c - a) + c (a - b)
या x + y + z = ab - ac + bc - ab + ac - bc
या x + y + z = 0
∴ x³ + y³ + z³ = 3xyz.
अर्थात् {a (b - c)}}³ + {b (c - a)}³ + {c (a - b)}³ = 3 a (b - c) × b (c - a) × c (a - b)
⇒ a³ (b - c)³ + b³ (c - a)³ + c³ (a - b)³
= 3abc (a - b) (b - c) (c - a)

प्रश्न 4.
x³ - 8y³ - 36xy - 216 का मान ज्ञात कीजिए यदि x = 2y + 6 है।
हल:
प्रश्नानुसार x³ - 8y³ - 36xy - 216
या x³ - 8y³ - 216 - 36xy
या (x)³ + (-2y)³ + (-6)³ - 3 (x) (- 2y) (-6)
= (x - 2y - 6) [(x)² + (-2y)² + (- 6)² - (x) (-2y) - (- 2y) (-6) - (-6) (x)]
= (x - 2y – 6) (x² + 4y² + 36 + 2xy - 12y + 6x)
∵ x = 2y + 6
∵ (27 + 6 - 2y - 6) (x² + 4y² + 36 + 2xy - 12y + 6x) = 0
(x² + 4y² + 36 + 2xy - 12y + 6x)
= 0

प्रश्न 5.
यदि बहुपद व्यंजक px² + 5x + r के गुणनखण्ड (x - 2) तथा (x - \(\frac{1}{2}\)) हों तो प्रदर्शित करो कि p = r.
हल:
रश्नानुसार f (x) = px² + 5x + r के दो गुणनखण्ड (x - 2) तथा \(\left(x-\frac{1}{2}\right)\) हैं।
∴ f (2) = 0 तथा f\(\left(\frac{1}{2}\right)\) = 0
[∵ x - 2 = 0 ⇒ x = 2
तथा x - 1 = 0 ⇒ x = \(\frac{1}{2}\)
⇒ p × (2)² + 5 × 2 + r = 0 तथा p\(\left(\frac{1}{2}\right)^{2}\) + 5 × 2 + r = 0
⇒ 4p + 10 + r = 0 तथा \(\frac{p}{4}+\frac{5}{2}\) + r = 0
⇒ 4p + r = - 10 तथा \(\frac{p+4 r+10}{4}\) = 0
⇒ 4p + r = - 10 तथा p + 4r + 10 = 0
⇒ 4p + r = - 10 तथा p + 4r = - 10
⇒ 4p + r = p + 4r
[∵ दोनों समीकरणों का RHS बराबर है।]
⇒ 3p = 3r
⇒ p = r (इतिसिद्धम् )

प्रश्न 6.
यदि बहुपद 9p³ - 27p² - 100p + 300 का एक गुणनखण्ड (3p + 10) है तो बहुपद के गुणनखण्ड ज्ञात कीजिए।
हल:
प्रश्न में दिएं बहुपद के गुणनखण्ड ज्ञात करने के लिए 9p³ - 27p² - 100p + 300 में 3p + 10 का भाग देने पर

∴ f (p) = 9p³ - 27p² - 100p + 300
= (3p + 10) (3p² - 19p + 30)
= (3p + 10) [3p² - 10p - 9p + 30]
= (3p + 10) [p(3p – 10) – 3 (3p – 10)]
f(p) = (3p + 10) (3p - 10) (p - 3)