RBSE Class 9 Maths Important Questions Chapter 15 प्रायिकता

Rajasthan Board RBSE Class 9 Maths Important Questions Chapter 15 प्रायिकता Important Questions and Answers.

RBSE Class 9 Maths Chapter 15 Important Questions प्रायिकता

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
किसी निश्चित घटना की प्रायिकता होगी
(A) 0
(B) \(\frac{1}{2}\)
(C) 1
(D) 2
उत्तरः
(C) 1

प्रश्न 2.
एक पासे को फेंकने पर 3 का अंक आने की प्रायिकता होगी
(A) \(\frac{1}{6}\)
(B) \(\frac{2}{3}\)
(C) \(\frac{5}{6}\)
(D) \(\frac{1}{3}\)
उत्तरः
(A) \(\frac{1}{6}\)

प्रश्न 3.
तीन पासों की फेंक में तीनों पर समान अंक आने की प्रायिकता है
(A) \(\frac{1}{36}\)
(B) \(\frac{3}{22}\)
(C) \(\frac{1}{6}\)
(D) \(\frac{1}{18}\)
उत्तरः
(A) \(\frac{1}{36}\)

प्रश्न 4.
एक ताश की गड्डी में से एक काला पत्ता खींचने की प्रायिकता होगी
(A) \(\frac{1}{52}\)
(B) \(\frac{1}{2}\)
(C) \(\frac{1}{26}\)
(D) \(\frac{25}{26}\)
उत्तरः
(B) \(\frac{1}{2}\)

प्रश्न 5.
एक पंक्ति में यादृच्छिक रूप से 10 विद्यार्थी बैठे हैं। दो विशेष प्रकार के विद्यार्थी पास-पास नहीं बैठने की प्रायिकता है
(A) \(\frac{1}{5}\)
(B) \(\frac{2}{5}\)
(C) \(\frac{3}{5}\)
(D) \(\frac{4}{5}\)
उत्तरः
(D) \(\frac{4}{5}\)

प्रश्न 6.
चार सिक्के उछालने पर तीन सिक्कों पर चित आने की प्रायिकता है
(A) \(\frac{3}{4}\)
(B) \(\frac{3}{8}\)
(C) \(\frac{1}{4}\)
(D) \(\frac{1}{8}\)
उत्तरः
(C) \(\frac{1}{4}\)

प्रश्न 7.
ताश के 52 पत्तों में यादृच्छिक रूप से एक पत्ता चुने जाने पर उसके हुकुम का पत्ता होने की प्रायिकता है
(A) \(\frac{1}{13}\)
(B) \(\frac{1}{2}\)
(C) \(\frac{3}{4}\)
(D) \(\frac{1}{4}\)
उत्तरः
(A) \(\frac{1}{13}\)

प्रश्न 8.
एक लीप वर्ष में 53 रविवार आने की प्रायिकता है
(A) \(\frac{2}{7}\)
(B) \(\frac{1}{7}\)
(C) \(\frac{5}{7}\)
(D) \(\frac{6}{7}\)
उत्तरः
(A) \(\frac{2}{7}\)

प्रश्न 9.
ताश के 52 पत्तों में से एक पत्ता खींचा जाता है। पत्ते के गुलाम, बेगम या बादशाह होने की प्रायिकता है
(A) \(\frac{1}{13}\)
(B) \(\frac{2}{13}\)
(C) \(\frac{3}{13}\)
(D) \(\frac{4}{13}\)
उत्तरः
(C) \(\frac{3}{13}\)

प्रश्न 10.
दो पासों को फेंकने पर अंकों का योग 12 आने की प्रायिकता होगी
(A) \(\frac{1}{3}\)
(B) \(\frac{1}{36}\)
(C) \(\frac{2}{3}\)
(D) \(\frac{35}{36}\)
उत्तरः
(B) \(\frac{1}{36}\)

प्रश्न 11.
किसी असम्भव घटना की प्रायिकता होती है
(A) 0
(B) 1
(C) 0 से कम
(D) 1 से अधिक
उत्तरः
(A) 0

प्रश्न 12.
निम्न में से कौनसी संख्या किसी घटना की प्रायिकता नहीं हो सकती?
(A) \(\frac{1}{2}\)
(B) \(\frac{2}{5}\)
(C) \(\frac{5}{4}\)
(D) 1
उत्तरः
(C) \(\frac{5}{4}\)

प्रश्न 13.
दो सिक्कों को उछालने पर अधिकतम एक चित आने की प्रायिकता होगी-
(A) \(\frac{1}{4}\)
(B) \(\frac{1}{2}\)
(C) \(\frac{3}{4}\)
(D) \(\frac{1}{4}\)
उत्तरः
(C) \(\frac{3}{4}\)

प्रश्न 14.
एक सिक्का 1000 बार उछाला जाता है । यदि पट आने की प्रायिकता है है तब कितनी बार चित आया?
(A) 625
(B) 375
(C) 525
(D) 725
उत्तरः
(A) 625

प्रश्न 15.
एक पासे को 100 बार फेंका जाता है। यदि सम संख्या ज्ञात करने की प्रायिकता है, तब विषम संख्या कितनी बार आएगी?
(A) 50
(B) 60
(C) 70
(D) 65
उत्तरः
(B) 60

रिक्त स्थानों की पूर्ति करो

प्रश्न 1.
किसी भी घटना के घटित होने की प्रायिकता .............. और ............. के बीच होती है।
उत्तर:
0 एवं 1

प्रश्न 2.
किसी भी सन्दर्भ का प्रयोग जिसका कई सम्भावित परिणामों में से एक परिणाम अवश्य होता है, एक ............... कहलाता है।
उत्तर:
अभिप्रयोग

प्रश्न 3.
एक ऐसा प्रयोग, जिसके सभी सम्भावित परिणाम विदित हों, परन्तु कौन सा परिणाम आएगा निश्चित न हो, एक ............... प्रयोग कहलाता है।।
उत्तर:
यादृच्छिक

प्रश्न 4.
वे परिणाम, जो किसी घटना के घटित होने को दर्शाते हैं, इस घटना के .................. परिणाम कहलाते हैं।
उत्तर:
अनुकूल

प्रश्न 5.
किसी निश्चित घटना के घटित होने की प्रायिकता ................. होती है।
उत्तर:
1

प्रश्न 6.
जब किसी घटना के घटित होने की प्रायिकता शून्य हो, तो वह घटना ......................... घटना कहलाती है।
उत्तर:
असम्भव

प्रश्न 7.
एक पासे के फेंकने पर 3 आने की प्रायिकता ................ होती है।
उत्तर:
\(\frac{1}{6}\)

प्रश्न 8.
एक पासे के फेंकने पर 3 का गुणज आने की प्रायिकता ..................... होती है।
उत्तर:
\(\frac{1}{3}\)

सत्य/असत्य-निम्नलिखित कथनों के लिए सत्य अथवा असत्य लिखिए

प्रश्न 1.
किसी प्रयोग के सभी सम्भावित परिणामों का संकलन प्रतिदर्श समष्टि कहलाता है।
उत्तर:
सत्य

प्रश्न 2.
किसी सिक्के को उछालने पर चित आने की प्रायिकता \(\frac{1}{4}\) होती है।
उत्तर:
असत्य

प्रश्न 3.
ताश की गड्डी में से एक पत्ता निकाला जाता है। इस पत्ते के लाल रंग का होने की प्रायिकता \(\frac{1}{2}\) होती है।
उत्तर:
सत्य

प्रश्न 4.
एक पासे को उछालने पर अभाज्य संख्या आने की प्रायिकता \(\frac{1}{2}\) होती है।
उत्तर:
सत्य

प्रश्न 5.
किसी.यदृच्छया प्रयोग से केवल तीन सम्भावित परिणाम A, B व C प्राप्त होते हैं तब (A) + P(B) + P(C) = 0
उत्तर:
असत्य

प्रश्न 6.
एक थैले में 6 नीली, 5 हरी व 8 नारंगी गेंदें हैं। इनमें से लाल गेंद निकलने की प्रायिकता 0 होगी।
उत्तर:
सत्य

प्रश्न 7.
किसी घटना की प्रायिकता ऋणात्मक भी हो सकती है।
उत्तर:
असत्य

प्रश्न 8.
घटना E के घटने की आनुभविक प्रायिकता P(E) है तो P(E) =

उत्तर:
असत्य

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
एक सिक्के को दो बार उछाला जाता है। दोनों बार चित आने की प्रायिकता लिखिए।
उत्तर = \(\frac{1}{4}\)

प्रश्न 2.
एक पासे के उछाल में 3 से छोटा अंक आने की प्रायिकता ज्ञात कीजिए।
उत्तर:
एक पासा फेंकने पर 1 से 6 तक कोई भी अंक आ सकता है। अतः कुल नि:शेष स्थितियाँ 6 होंगी। यहाँ पर घटना 3 से छोटा अंक आना है। स्पष्ट है कि पासे की फेंक में 1 या 2 अंक आना है अर्थात् अनुकूल स्थितियाँ 2 होंगी।
अतः प्रायिकता (P) = \(\frac{2}{6}\) = \(\frac{1}{3}\).

प्रश्न 3.
एक लीप वर्ष में केवल 52 मंगलवार आने की प्रायिकता ज्ञात कीजिए।
हल:
प्रायिकता (P) = \(\frac{5}{7}\)

प्रश्न 4.
एक पासे के फेंकने पर सम अंक आने की प्रायिकता ज्ञात कीजिए।
हल:
अनुकूल स्थितियाँ (2, 4, 6) = 3
कुल स्थितियाँ = 6
∴ प्रायिकता (P) = \(\frac{3}{6}\) = \(\frac{1}{2}\)

प्रश्न 5.
एक ताश की गड्डी से एक पत्ता निकाला जाता है। इसके इक्का होने की प्रायिकता ज्ञात करो।
हल:
ताश की गड्डी में कुल पत्तों की संख्या = 52
ताश की गड्डी में इक्कों की संख्या = 4
∴ इक्का होने की प्रायिकता = \(\frac{4}{52}\) = \(\frac{1}{13}\)

प्रश्न 6.
एक सिक्के को 1000 बार उछालने पर निम्नलिखित बारम्बारताएँ प्राप्त होती हैं।
चित: 455, पट : 545
प्रत्येक घटना की प्रायिकता ज्ञात कीजिए।
हल:
चित आने की प्रायिकता

लघूत्तरात्मक एवं निबन्धात्मक प्रश्न

प्रश्न 1.
एक टेलीफोन निर्देशिका के एक पृष्ठ पर 200 टेलीफोन नम्बर हैं। उनके इकाई स्थान वाले अंक का बारम्बारता बंटन (उदाहरण के लिए संख्या 25828573 में इकाई के स्थान पर अंक 3 है) सारणी में दिया गया है|

पृष्ठ को देखे बिना, इन संख्याओं में से किसी एक संख्या पर अपनी पेंसिल रख दीजिए, अर्थात् संख्या को यदृच्छया चुना गया है। इकाई के स्थान पर अंक 6 के होने की प्रायिकता क्या होगी?
हल:
इकाई के स्थान पर अंक 6 के होने की प्रायिकता

इसी प्रकार, आप उन संख्याओं के आने की प्रायिकता प्राप्त कर सकते हैं जिनमें इकाई के स्थान पर कोई अन्य अंक हो।

प्रश्न 2.
एक मौसम केन्द्र के रिकार्ड को देखने से पता चलता है कि पिछले 250 क्रमागत दिनों में किए गए मौसम पूर्वानुमानों में से 175 बार उसके पूर्वानुमान सही रहे हैं।
(i) एक दिए हुए दिन पर पूर्वानुमान के सही होने की प्रायिकता क्या होगी?
(ii) दिए हुए दिन पर पूर्वानुमान के सही न होने की प्रायिकता क्या होगी?
हल:
दिनों की कुल संख्या जिनके रिकार्ड उपलब्ध हैं = 250
(i) P(दिए हुए दिन पर पूर्वानुमान सही था)

= \(\frac{175}{250}\) = 0.7

(ii) उन दिनों की संख्या जिस दिन का पूर्वानुमान सही नहीं था
= 250 - 175 = 75
अतः, P(दिए हुए दिन पर पूर्वानुमान सही नहीं था)
= \(\frac{75}{250}\) = 0.3

ध्यान दीजिए कि-
P(दिए हुए दिन का पूर्वानुमान सही था) + P (दिए हुए दिन का पूर्वानुमान सही नहीं था)
= 0.7 + 0.3 = 1

प्रश्न 3.
एक विद्यार्थी द्वारा मासिक यूनिट परीक्षा में प्राप्त किए गए अंकों का प्रतिशत नीचे दिया गया हैं

इन आँकड़ों के आधार पर इस बात की प्रायिकता ज्ञात कीजिए कि एक यूनिट परीक्षा में वह विद्यार्थी 70% से अधिक अंक प्राप्त करता है।
हल:
ली गई यूनिट परीक्षाओं की कुल संख्या 5 है।
उन यूनिट परीक्षाओं की संख्या, जिनमें विद्यार्थी 70% से अधिक अंक प्राप्त करता है, 3 है।
अतः P(70% से अधिक अंक प्राप्त करना)
= \(\frac{3}{5}\) = 0.6

प्रश्न 4.
बीजों के 5 थैलों में से प्रत्येक थैले से पचास बीज यदृच्छया चुनकर उन्हें ऐसी मानकीकृत अवस्थाओं में रखा गया जो अंकुरण के अनुकूल हैं। 20 दिन बाद प्रत्येक संग्रह में अंकुरित हुए बीजों की संख्या गिन कर नीचे दर्शाए अनुसार एक सारणी में लिखी गई।

निम्नलिखित बीजों के अंकुरण की प्रायिकता क्या है?
(i) एक थैले में 40 से अधिक बीज
(ii) एक थैले में 49 बीज
(iii) एक थैले में 35 से अधिक बीज।
हल:
थैलों की कुल संख्या 5 है।
(i) उन थैलों की संख्या, जिनमें 50 बीजों में से 40 से अधिक बीज अंकुरित हुए हैं, 3 है।
अतः, P(एक थैले में 40 से अधिक बीजों का अंकुरण) = \(\frac{3}{5}\) = 0.6

(ii) उन थैलों की संख्या जिनमें 49 बीज अंकुरित हुए हैं, 0 है। अतः, P(एक थैले के 49 बीजों का अंकुरण)
= \(\frac{0}{5}\) = 0

(iii) उन थैलों की संख्या, जिनमें 35 से अधिक बीज अंकुरित हुए हैं, 5 है।
अतः, अपेक्षित प्रायिकता = \(\frac{5}{5}\) = 1

प्रश्न 5.
बारम्बारता बंटन सारणी (अध्याय 14 के उदाहरण 4 की सारणी 14.3) लीजिए जिसमें एक कक्षा के 38 विद्यार्थियों के भार दिए गए हैं।
(i) इस बात की प्रायिकता ज्ञात कीजिए जिसमें कक्षा के एक विद्यार्थी का भार (kg में) अन्तराल 46-50 स्थित हो।
(ii) इस सन्दर्भ में ऐसी दो घटनाएँ बताइए जिनमें एक की प्रायिकता 0 हो और दूसरी की प्रायिकता 1 हो।
हल:
(i) विद्यार्थियों की कुल संख्या 38 है और । 40-45 kg के भार वाले विद्यार्थियों की संख्या 3 है। अतः, P(विद्यार्थी का भार 46-50 kg है)
= \(\frac{3}{38}\) = 0.079

(ii) उदाहरण के लिए वह घटना लीजिए जिसमें विद्यार्थी का भार 30 kg है। क्योंकि किसी भी विद्यार्थी का भार 30 kg नहीं है, इसलिए इस घटना के घटने की प्रायिकता 0 होगी। इसी प्रकार, एक विद्यार्थी का 30 kg से अधिक भार होने की प्रायिकता \(\frac{38}{38}\) = 1 है।

प्रश्न 6.
टायर बनाने वाली एक कम्पनी तय की गई उन दूरियों का एक रिकार्ड रखती थी, जिसके पहले टायर को बदल देने की आवश्यकता पड़ी। सारणी में 1000 स्थितियों के परिणाम दिखाए गए हैं।

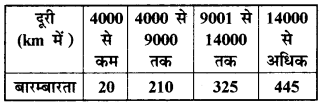
यदि आप इस कम्पनी से एक टायर खरीदते हैं, तो इस बात की प्रायिकता क्या होगी कि
(i) 4000 km की दूरी तय करने से पहले ही इसे बदलना आवश्यक होगा?
(i) यह 9000 km से भी अधिक दूरी तक चलेगा?
(iii) 4000 km और 14000 km के बीच की कोई दूरी तय करने के बाद इसे बदलना आवश्यक होगा?
हल:
अभिप्रयोगों की कुल संख्या = 1000
(i) उस टायरं की बारम्बारता, जिसे 4000 km की दूरी तय करने से पहले बदलना आवश्यक हो, 20 है।
अतः, P(4000 km की दूरी तय करने से पहले टायर बदलना आवश्यक हो)
= \(\frac{20}{1000}\) = 0.02

(ii) उस टायर की बारम्बारता जो 9000 km से भी अधिक दूरी तय करेगा
= 325 + 445 = 770
अतः, P(टायर 9000 km से भी अधिक दूरी तक चलेगा) = \(\frac{770}{1000}\) = 0.77

(iii) उस टायर की बारम्बारता जिसे 4000 km और 14000 km के बीच की कोई दूरी तय कर लेने के बाद बदलना आवश्यक होगा = 210 + 325 = 535
अतः, P(4000 km और 14000 km के बीच की कोई दूरी तय करने के बाद टायर को बदलना आवश्यक हो) = \(\frac{535}{1000}\) = 0.535

प्रश्न 7.
एक पासे को 1000 बार फेंकने पर प्राप्त परिणामों 1, 2, 3, 4, 5 और 6 की बारम्बारताएँ सारणी में दी गई हैं

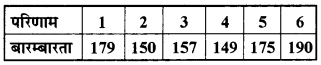
प्रत्येक परिणाम के प्राप्त होने की प्रायिकता ज्ञात कीजिए।
हल:
मान लीजिए E, परिणाम के प्राप्त होने की घटना को प्रकट करता है, जहाँ 1 = 1, 2, 3, 4, 5, 6 है। तब,
परिणाम 1 की प्रायिकता = P(E₁)

ध्यान दीजिए कि P(E₁) + P(E₂) + P(E₃) + P(E₄) + P(E₅) + P(E₆) = 1 है।
साथ ही, यह भी देखिए कि
(i) प्रत्येक घटना की प्रायिकता 0 और 1 के बीच होती है।
(ii) सभी प्रायिकताओं का योगफल 1 होता है।
(iii) E₁, E₂, ......, E₆ में एक अभिप्रयोग के सभी सम्भव परिणाम आ जाते हैं।

प्रश्न 8.
एक बीमा कम्पनी ने आयु और दुर्घटनाओं के बीच के सम्बन्ध को ज्ञात करने के लिए एक विशेष नगर के 2000 ड्राइवरों का यदृच्छया चयन किया (किसी ड्राइवर को कोई विशेष वरीयता दिए बिना)। प्राप्त किए गए आँकड़े नीचे सारणी में दिए गए हैं

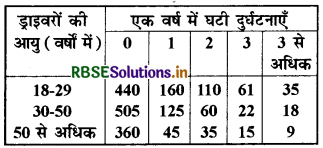
नगर से यदृच्छया चुने गए एक ड्राइवर के लिए निम्नलिखित घटनाओं की प्रायिकताएँ ज्ञात कीजिए
(i) 18-29 वर्ष की आयु का जिसके साथ एक वर्ष में ठीक-ठीक 3 दुर्घटनाएँ घटी हैं।
(ii) 30-35 वर्ष की आयु का जिसके साथ एक वर्ष में एक या अधिक दुर्घटनाएँ घटी हैं।
(iii) जिसके साथ एक वर्ष में कोई दुर्घटना नहीं घटी।
हल:
ड्राइवरों की कुल संख्या = 2000
(i) उन ड्राइवरों की संख्या, जिनकी आय 18-29 वर्ष है और जिनके साथ एक वर्ष में ठीक-ठीक तीन दुर्घटनाएँ घटी हैं, 61 है।
अतः, P(ड्राइवर 18-29 वर्ष का हो जिसके साथ ठीक-ठीक तीन दुर्घटनाएँ घटीं)
= \(\frac{61}{2000}\)
= 0.0305 ≈ 0.031

(ii) उन ड्राइवरों की संख्या, जिनकी आयु 30-50 | वर्ष है और जिनके साथ एक वर्ष में एक या अधिक दुर्घटनाएँ घटी हैं, 125 + 60 + 22 + 18, अर्थात् 225 है।
अतः, P(ड्राइवर 30-50 वर्ष का हो और जिसके साथ एक या अधिक दुर्घटनाएँ घटी हैं)
= \(\frac{225}{2000}\) = 0.1125 = 0.113

(iii) उन ड्राइवरों की संख्या जिनके साथ एक वर्ष में कोई दुर्घटना नहीं घटी
= 440 + 505 + 360 = 1305
अतः, P(ड्राइवर जिनके साथ कोई दुर्घटना नहीं घटी) = \(\frac{1305}{2000}\) = 0.653

प्रश्न 9.
एक पासे को फेंकने पर 4 से बड़ा अंक आने की प्रायिकता ज्ञात कीजिए।
हल:
एक पासे को फेंकने पर 6 प्रकार के अंक आने की सम्भावना रहती है। अतः घटना की निःशेष स्थितियाँ = 6
प्रदत्त घटना के लिए 4 से बड़े अंक 5 व 6 होंगे जिनके आने की अनुकूल स्थितियाँ = 2
∴ अभीष्ट प्रायिकता (P) = \(\frac{2}{6}\) = \(\frac{1}{3}\)

प्रश्न 10.
एक अलीप वर्ष में केवल 52 रविवार आने की प्रायिकता ज्ञात कीजिए।
हल:
अलीप वर्ष में दिनों की संख्या = 365
∴ सप्ताहों की संख्या = \(\frac{365}{7}\)
= 52 सप्ताह तथा 1 दिन शेष यहाँ 52 सप्ताह का अर्थ है कि अलीप वर्ष में 52 रविवार तो होंगे ही। अब 1 शेष दिन निम्न में से कोई भी हो सकता है-रविवार, सोमवार, मंगलवार, बुधवार, गुरुवार, शुक्रवार, शनिवार
इनकी कुल स्थितियाँ = 1
∴ नि:शेष स्थितियाँ = 7
अब 52 रविवार तो अलीप वर्ष में होते ही हैं। इसलिए शेष 1 दिन रविवार न होकर अन्य दिवस होना चाहिए।
अतः अनुकूल स्थितियाँ = 6
∴ अलीप वर्ष में 52 रविवार आने की प्रायिकता
(P) = \(\frac{6}{7}\)