RBSE Class 9 Maths Important Questions Chapter 14 सांख्यिकी

Rajasthan Board RBSE Class 9 Maths Important Questions Chapter 14 सांख्यिकी Important Questions and Answers.

RBSE Class 9 Maths Chapter 14 Important Questions सांख्यिकी

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
सांख्यिकी के अध्ययन के लिए संकलित आंकड़ों के प्रकार होते हैं
(A) एक
(B) दो
(C) तीन
(D) सभी
उत्तर:
(C) तीन

प्रश्न 2.
दण्ड लेखाचित्र में आयत की ऊँचाई होती है
(A) वर्ग की आवृत्ति के व्युत्क्रमानुपात में
(B) वर्ग की आवृत्ति के समानुपात में
(C) वर्ग अन्तराल के समानुपात में
(D) वर्ग अन्तराल के व्युत्क्रमानुपात में
उत्तर:
(B) वर्ग की आवृत्ति के समानुपात में

प्रश्न 3.
विद्यालय की किसी कक्षा के परीक्षा परिणाम का तुलनात्मक अध्ययन किया जा सकता है
(A) वृत्ताकार लेखाचित्र से
(B) दण्ड लेखाचित्र से
(C) रैखिक लेखाचित्र से
(D) उपर्युक्त सभी से
उत्तर:
(B) दण्ड लेखाचित्र से

प्रश्न 4.
किसी बंटन का परास 50 है तथा वर्ग अन्तराल 10 है तो वर्गों की संख्या होगी
(A) 6
(B) 10
(C) 5
(D) 4
उत्तर:
(C) 5

प्रश्न 5.
बंटन 2, 3, 8, 4, 3, 8, 9, 3, 2, 1, 6 का परास
(A)7
(B) 8
(C) 6
(D) 4
उत्तर:
(B) 8

प्रश्न 6.
यदि विचर का बंटन 4, 5, 6, 3, 2, 5, 1, 5 हो
तो विचर 5 की बारम्बारता होगी
(A) 3
(B) 4
(C)2
(D) 1
उत्तर:
(A) 3

प्रश्न 7.
रिलायन्स कप-क्रिकेट प्रतियोगिता के सेमीफाइनल मैच में भारतीय टीम के खिलाड़ियों ने निम्न रन बनाए 4, 34, 64, 24, 34, 37, 2, 3, 7, 4,0 'उपर्युक्त आँकड़ों के आधार पर वर्ग 0-10 की बारम्बारता होगी
(A) 6
(B) 5
(C) 11
(D) अनन्त
उत्तर:
(A) 6

प्रश्न 8.
निम्न बंटन में| वर्ष

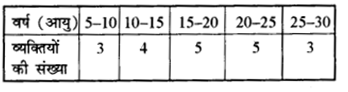
20 वर्ष से कम आयु के व्यक्तियों की संख्या
(A) 5
(B) 10
(C) 12
(D) 15
उत्तर:
(C) 12

प्रश्न 9.
निम्नलिखित आँकड़ों में वर्ग 20-25 की बारम्बारता है
15, 23, 31, 27, 24, 20, 18, 22, 19, 25, 30, 16, 33, 22, 26, 35, 18, 21, 27, 17.
(A) 6
(B) 7
(C) 5
(D) 4
उत्तर:
(A) 6

प्रश्न 10.
5, 3, 9, 8, 7, 2, 11 की माध्यक होगी-
(A) 11
(B) 8
(C) 7
(D) 7
उत्तर:
(C) 7

प्रश्न 11.
निम्न में से कौनसी ग्राफीय विधि सांख्यिकी आँकड़ों को प्रदर्शित करने की नहीं है-
(A) दण्ड आलेख
(B) आयत चित्र
(C) बारम्बारता बहुभुज
(D) संचयी बारम्बारता बंटन
उत्तर:
(D) संचयी बारम्बारता बंटन

प्रश्न 12.
अवर्गीकृत आँकड़ों की केन्द्रीय प्रवृत्ति के माप
(A) मध्य
(B) माध्यक
(C) बहुलक
(D) उपर्युक्त सभी
उत्तर:
(D) उपर्युक्त सभी

प्रश्न 13.
किसी भी आयत चित्र में, प्रत्येक आयत का आधार है
(A) बारम्बारता
(B) वर्ग अन्तराल
(C) परास
(D) वर्ग अन्तराल का आकार
उत्तर:
(B) वर्ग अन्तराल

प्रश्न 14.
किसी आयत चित्र में वर्ग अन्तराल या समूह लिए जाते हैं
(A) y-अक्ष के साथ
(B) x-अक्ष के साथ
(C) दोनों x व y अक्ष के साथ
(D) x व y अक्ष के मध्य
उत्तर:
(B) x-अक्ष के साथ

प्रश्न 15.
एक कक्षा के 9 विद्यार्थियों की (सेमी. में) लम्बाइयाँ हैं-
155, 160, 145, 149, 150, 147, 152, 144, 148
इन आँकड़ों का माध्यक है-
(A) 149
(B) 148
(C) 160
(D) 145
उत्तर:
(A) 149

रिक्त स्थानों की पूर्ति करो

प्रश्न 1.
एक निश्चित उद्देश्य से एकत्रित किए गए तथ्यों या अंकों को ............................. कहा जाता है।
उत्तर:
आँकड़े

प्रश्न 2.
सबसे अधिक बार आने वाला प्रेक्षण ........................ कहलाता है।
उत्तर:
बहुलक

प्रश्न 3.
प्रेक्षणों के सभी मानों के योग को प्रेक्षणों की कुल संख्या से भाग देने पर ............................ प्राप्त होता है।
उत्तर:
माध्य

प्रश्न 4.
यदि n विषम है, तो माध्यक = ............................ वें प्रेक्षण का मान।
उत्तर:
\(\left(\frac{n+1}{2}\right)\)

प्रश्न 5.
यदि कोई अनुसंधानकर्ता किसी उद्देश्य या योजना को ध्यान में रखकर स्वयं आँकड़ों का संग्रह करता है तो प्राप्त आँकड़े ............................. आँकड़े कहलाते हैं।
उत्तर:
प्राथमिक

सत्य/असत्य-निम्नलिखित कथनों के लिए सत्य अथवा असत्य लिखिए

प्रश्न 1.
आँकड़ों की परास ऋणात्मक हो सकती है।
उत्तर:
असत्य

प्रश्न 2.
प्रेक्षण 30 को वर्णअन्तराल 30-40 में लिया जाता
उत्तर:
सत्य

प्रश्न 3.
दण्ड आलेख को क्षैतिज या ऊर्ध्वाधर दोनों प्रकार से बनाया जा सकता है।
उत्तर:
सत्य

प्रश्न 4.
6, 5, 3, 5, 6, 5, 8 का बहुलक 8 है क्योंकि 8 सबसे बड़ी संख्या है।
उत्तर:
असत्य

प्रश्न 5.
किसी भी प्रेक्षण का माध्य सदैव माध्यम से कम होता है।
उत्तर:
असत्य

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
यदि 5, 8, 4, x, 6, 9 अंकों का समान्तर माध्य 7 हो, तो x का मान बताइए।
हल:

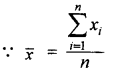
अर्थात् \(\frac{5+8+4+x+6+9}{6}=\frac{7}{1}\)
या 32 + x = 42
या x = 42 - 32
∴x = 10

प्रश्न 2.
संकलन की दृष्टि से आँकड़े कितने प्रकार के होते हैं?
उत्तर:
संकलन की दृष्टि से आँकड़े दो प्रकार के होते हैं

• प्राथमिक आँकड़े
• द्वितीयक आँकड़े।

प्रश्न 3.
वर्गीकरण का अर्थ लिखिए।
उत्तर:
आँकड़ों को उनके गुण तथा विशेषताओं के आधार पर विभिन्न समूहों (वर्गों) में विभाजित करने की प्रक्रिया को वर्गीकरण कहते हैं।

प्रश्न 4.
परास किसे कहते हैं ?
उत्तर:
विचर x के अधिकतम मान तथा न्यूनतम मान के अन्तर को परास कहते हैं।

प्रश्न 5.
आयतचित्र किसे कहते हैं ?
उत्तर:
वह लेखाचित्र जिसमें किसी श्रेणी की बारम्बारता बराबर एक-दूसरे से सटे हुए आयतों द्वारा दर्शायी जाती है, उसे आयतचित्र कहते हैं।

प्रश्न 6.
बंटन 3, 5, 7, 4, 2, 1, 4, 3, 4 का बहुलक लिखिए।
उत्तर:
उपर्युक्त बंटन में 4 सर्वाधिक 3 बार आया है अत: बहुलक = 4

प्रश्न 7.
किसी बारम्बारता बंटन का समान्तर माध्य 18.50 है तथा Σf = 20 हो, तो Σfx का मान लिखिए।
हल:
Σfx = 18.50 × 20 = 370

प्रश्न 8.
2.3, 3.4, 1.2, 7.8, 8.9, 4.5, 5.6 के माध्यक का मान लिखिए।
हल:
आरोही क्रम = 1.2, 2.3, 3.4, 4.5, 5.6, 7.8, 8.9 .
माध्यक = \(\left(\frac{\mathrm{N}+1}{2}\right)\) वाँ पद = \(\left(\frac{7+1}{2}\right)\) वाँ पद = चौथा पद
अर्थात् माध्यक = 4.5

प्रश्न 9.
100 मजदूरों की मजदूरी दी हुई है। यदि अधिकतम मजदूरी 250 रुपये तथा न्यूनतम मजदूरी 80 रुपये है और इसे दस वर्गों में विभाजित करते हैं तो विस्तार किस प्रकार ज्ञात किया जाएगा?
हल:
वर्ग विस्तार

= \(\frac{250-80}{10}\) = \(\frac{170}{10}\)

प्रश्न 10.
बंटन 1, 12, 6, 10, 4, 8, 4, 1 का माध्यक ज्ञात कीजिए।
हल:
आरोही क्रम = 1, 1, 4, 4, 6, 8, 10, 12
M = \( \left(\frac{N+1}{2}\right)\)वाँ पद = \(\left(\frac{8+1}{2}\right)\) वाँ पद = 4.5वाँ पद
अर्थात् M = \(\frac{4+6}{2}=\frac{10}{2}\) = 5
अतः माध्यक = 5

लघूत्तरात्मक प्रश्न

प्रश्न 1.
निम्न बारम्बारता बंटन की माध्यिका ज्ञात कीजिए-

हल:
संचयी बारम्बारता सारणी-

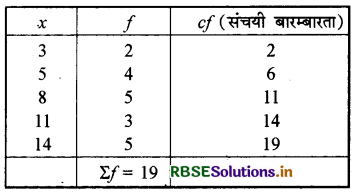
यहाँ N = Σf = 19 तब \(\frac{N}{2}\) = \(\frac{19}{2}\) = 9.5
9.5 से ठीक बड़ी संचयी बारम्बारता (c.f.) 11 है जिसके संगत चर का मान 8 है।
अतः माध्यिका M = 8 है।

प्रश्न 2.
यदि 5, 6, 2, 3, 1, 8, x, 9, 2 अंकों का समान्तर माध्य 5 हो, तो x का मान ज्ञात कीजिए।
हल:
यहाँ n = 9 तथा X̄ = 5
अतः \(\frac{5+6+2+3+1+8+x+9+2}{9}\) = 5
या \(\frac{36+x}{9}\) = 5
या 36 + x = 5 × 9.
या 36 + x = 45
या x = 45 - 36.
x = 9 अंक

प्रश्न 3.
बंटन 6, 8, 5, 9, 3, 7 की माध्यिका ज्ञात कीजिए।
हल:
विचर के दिये हुए मानों को आरोही क्रम में लिखने पर

∵ पदों की संख्या n = 6 सम संख्या है।
अतः M = दो मध्य पदों का समान्तर माध्य = तीसरे तथा चौथे पद के मानों का समान्तर माध्य
= \(\frac{5+9}{2}\)
= \(\frac{14}{2}\)
= 7

प्रश्न 4.
निम्न असमूहित बंटन का माध्य लिखिए

हल:

माध्य X̄ = \(\frac{\sum f x}{\sum f}\)
= \(\frac{76}{26}\) = 2.92

प्रश्न 5.
किसी खिलाड़ी द्वारा दस पारियों में बनाये गये रनों की संख्या निम्नलिखित है
50, 70, 80, 100, 60, 50, 40, 30, 50, 60 रनों का बहुलक ज्ञात कीजिए।
हल:

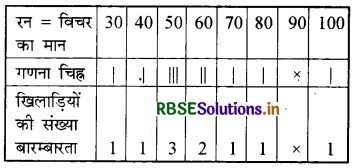
सारणी से स्पष्ट है कि सर्वाधिक बारम्बारता 3, विचर के मान 50 की है।
अतः रनों का बहुलक = 50 रन 

प्रश्न 6.
निम्न बंटन का बहुलक ज्ञात कीजिए
2, 1, 3, 4, 2, 5, 1, 1, 4, 3, 6, 7, 2, 8, 2, 9, 3, 10, 10, 2, 9, 3, 5, 2
हल:
दिए हुए बंटन को निम्न बारम्बारता सारणी द्वारा व्यक्त किया जा सकता है-

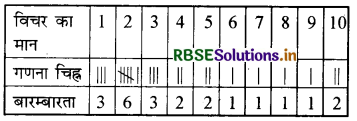
सारणी से स्पष्ट है कि सर्वाधिक बारम्बारता 6 विचर 2 की है।
अतः बहुलक 2 होगा।

प्रश्न 7.
निम्नलिखित सारणी में दूसरे तथा छठे वर्ग की निम्न सीमा एवं वर्ग अन्तराल बताइए

हल:
दूसरे वर्ग की निम्न सीमा = 5; वर्ग अन्तराल = 5 .
छठे वर्ग की निम्न सीमा = 25; वर्ग अन्तराल = 5

प्रश्न 8.
निम्नलिखित सारणी में

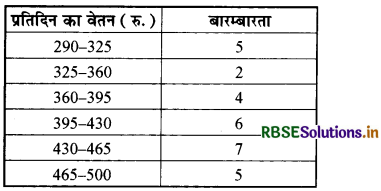
(i) चौथे वर्ग की ऊपरी सीमा लिखिए।
(ii) छठे वर्ग की निम्न सीमा लिखिए।
(iii) वर्ग अन्तराल लिखिए।
(iv) तीसरे वर्ग की बारम्बारता लिखिए। .
(v) 395-430 रु. प्रतिदिन प्राप्त करने वाले कार्मिकों की संख्या लिखिए।
हल:
(i) चौथे वर्ग की ऊपरी सीमा = 430 रु.
(ii) छठे वर्ग की निम्न सीमा = 465 रु.
(iii) वर्ग अन्तराल = 35 रु.
(iv) तीसरे वर्ग की बारम्बारता = 4
(v) 395-430 रु. प्रतिदिन प्राप्त करने वाले कार्मिकों की संख्या = 6

प्रश्न 9.
एक परीक्षा में कक्षा IX के 30 छात्रों के प्राप्तांक निम्नलिखित हैं। इन प्राप्तांकों से 10 वर्ग अन्तराल वाले 5 वर्गों की बारम्बारता सारणी बनाइए
19, 27, 40, 3, 33, 41, 18, 8, 20, 0, 23, 49, 16, 36, 14, 23, 49, 9, 35, 38, 23, 10, 37, 24, 22, 28, 29, 12, 6, 39.
हल:

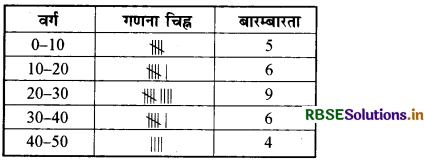
प्रश्न 10.
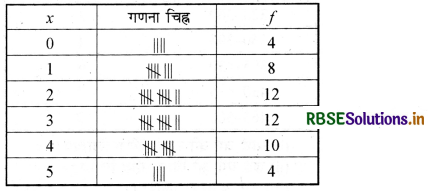
एक कक्षा के 50 छात्रों ने अंग्रेजी विषय के प्रथम टेस्ट में 5 अंकों में से क्रमशः निम्न प्रकार अंक प्राप्त किये
4, 3, 5, 1, 0, 4, 2, 1, 3, 3, 2, 4, 4, 5, 4, 5, 3, 2, 2, 1, 4, 3, 3, 2, 1, 0, 0, 5, 4, 3, 2, 1, 3, 3, 4, 4, 3, 2, 1, 1, 4, 2, 2, 3, 2, 2, 0, 1, 2, 3.
उपर्युक्त बंटन की बारम्बारता सारणी बनाइए।
हल:

निबन्धात्मक प्रश्न

प्रश्न 1.
नवीं कक्षा के 40 विद्यार्थियों से उनके जन्म का महीना बताने के लिए कहा गया। इस प्रकार प्राप्त आँकड़ों से निम्नलिखित आलेख बनाया गया-

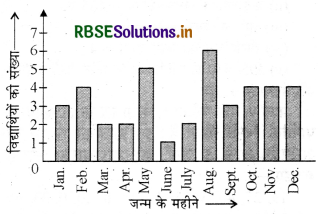
ऊपर दिए गए आलेख को देखकर निम्नलिखित प्रश्नों के उत्तर दीजिए
(i) नवम्बर के महीने में कितने विद्यार्थियों का जन्म हुआ?
(ii) किस महीने में सबसे अधिक विद्यार्थियों का जन्म हुआ?
हल:
ध्यान दीजिए कि यहाँ चर 'जन्म दिन का महीना' है और चर का मान 'जन्म लेने वाले विद्यार्थियों की संख्या' है।
(i) नवम्बर के महीने में 4 विद्यार्थियों का जन्म हुआ।
(ii) अगस्त के महीने में सबसे अधिक विद्यार्थियों का जन्म हुआ।

प्रश्न 2.
एक परिवार ने जिसकी मासिक आय 20,000 रु. है, विभिन्न मदों के अन्तर्गत हर महीने होने वाले खर्च की योजना बनाई थी:

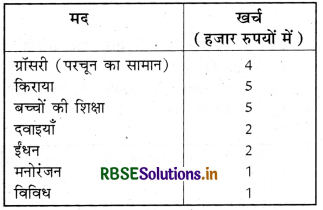
ऊपर दिए गए आँकड़ों का एक दण्ड आलेख बनाइए।
हल:
हम इन आँकड़ों का दण्ड आलेख निम्नलिखित चरणों में बनाते हैं। ध्यान दीजिए कि दूसरे स्तम्भ में दिया गया मात्रक (unit) 'हजार रुपयों में' है। अतः ग्रॉसरी (परचून का सामान) के सामने लिखा अंक 4 का अर्थ 4000 रु. है।
1. कोई भी पैमाना (scale) लेकर हम क्षैतिज अक्ष पर मदों (चर) को निरूपित करते हैं, क्योंकि यहाँ दण्ड की चौड़ाई का कोई महत्व नहीं होता। परन्तु स्पष्टता के लिए हम सभी दण्ड सामान चौड़ाई के लेते हैं और उनके बीच समान दूरी बनाए रखते हैं। माना 1 मद = 1 सेमी.

2. हम खर्च (मूल्य) को ऊर्ध्वाधर अक्ष पर निरूपित करते हैं। क्योंकि अधिकतम खर्च 5000 रु. है, इसलिए हम पैमाना 1 मात्रक = 1000 रु. ले सकते हैं।

3. अपने पहले मद अर्थात् ग्रॉसरी को निरूपित करने क लिए, हम 1 मात्रक की चौड़ाई 4 मात्रक की ऊँचाई वाला एक आयताकार दण्ड बनाते हैं।

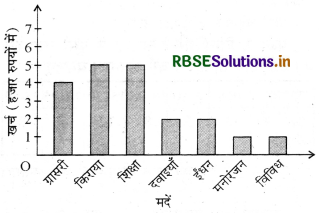
4. इसी प्रकार, दो क्रमागत दण्डों के बीच 1 मात्रक का खाली स्थान छोड़कर अन्य मदों को निरूपित किया जाता है।

प्रश्न 3.
नीचे दी गयी बारम्बारता बंटन सारणी में एक कक्षा के 36 विद्यार्थियों के भार दिये गये हैं। इसका आयत चित्र और बारम्बारता बहुभुज बनाइये।

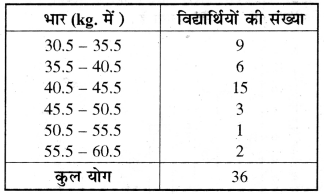
हल:
(1) यहाँ पर पहला वर्ग अन्तराल 30.5 से प्रारम्भ हो रहा है न कि शून्य से इसलिये हम एक निकुंच (kink) का चिह्न बनाकर या अक्ष में एक विच्छेद रेखा दिखाकर आलेख पर दर्शा सकते है। पैमाना 1 cm = 3 kg. ले सकते हैं।

(2) यहाँ पर अधिकतम बारम्बारता 15 है। इसलिये हमें एक ऐसे पैमाने का चयन करना होता है जिससे कि उसमें यह अधिकतम बारम्बारता आ सके।

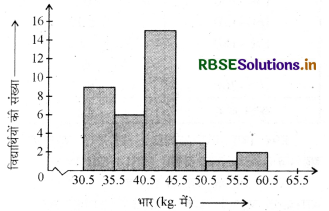
उपरोक्त आयत चित्र के संगत आयतों की ऊपरी भुजाओं के मध्य-बिन्दुओं को रेखाखण्डों से जोड़ दें और इनके मध्य बिन्दुओं को B, C, D, E, F तथा G से. अंकित करें। जब इन मध्य-बिन्दुओं को हम रेखाखण्डों से जोड़ देते हैं, तो हमें आकृति BCDEFG प्राप्त होती हैं।

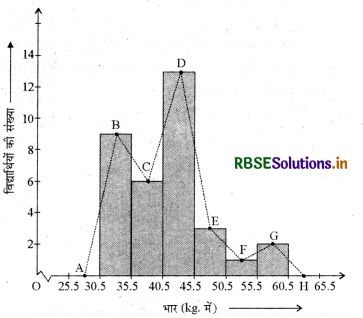
प्रश्न 4.
निम्न बंटन का एक आयत चित्र बनाइए-

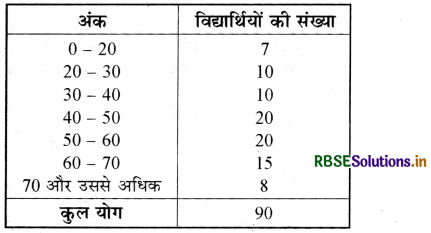
हल:

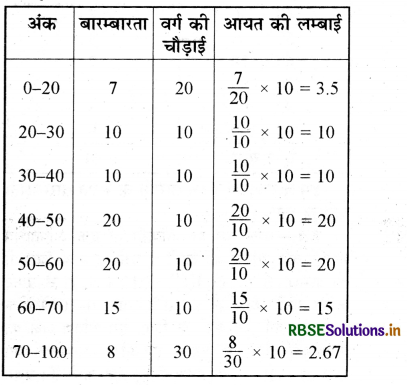
यहाँ पर हमने प्रत्येक स्थिति में 10 अंकों के अन्तराल पर ये लम्बाइयाँ परिकलित की हैं। इसलिए हम इन लम्बाइयों की प्रति 10 अंक अन्तराल पर विद्यार्थियों के समानुपाती मान सकते हैं।

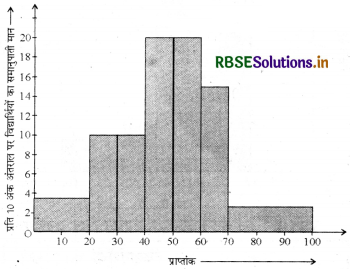
प्रश्न 5.
एक परीक्षा में एक कक्षा के 51 विद्यार्थियों द्वारा 100 में से प्राप्त किए अंक सारणी में दिए गए हैं-

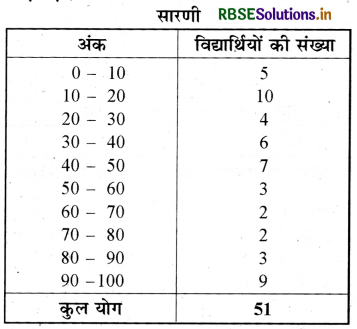
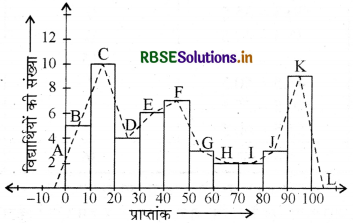
इस बारम्बारता बंटन सारणी के संगत बारम्बारता बहुभुज बनाइए।
हल:
पहले हम इन आँकड़ों से एक आयतचित्र बनाएँगे और आयतों की ऊपरी भुजाओं के मध्य-बिन्दुओं को क्रमशः B, C, D, E, F, G H, I, J, K से प्रकट करेंगे। यहाँ पहला वर्ग 0-10 है। अतः 0-10 से ठीक पहले का वर्ग ज्ञात करने के लिए, हम क्षैतिज अक्ष को ऋणात्मक दिशा में बढ़ाते हैं और काल्पनिक वर्ग अन्तराल (-10)-0 का मध्य-बिन्दु ज्ञात करते हैं। प्रथम अन्त बिन्दु (end point), अर्थात् B को क्षैतिज अक्ष की | ऋणात्मक दिशा में शून्य बारम्बारता वाले इस मध्य-बिन्दु | से मिला दिया जाता है। वह बिन्दु जहाँ यह रेखाखण्ड ऊर्ध्वाधर अक्ष से मिलता है, उसे A से प्रकट करते हैं। | मान लीजिए दिए हुए आँकड़ों के अन्तिम वर्ग के ठीक बाद वाले वर्ग का मध्य-बिन्दु L है। तब OABCDEFGHIJKL वांछित बारम्बारता बहुभुज है, | जिसे आकृति में दिखाया गया है।

प्रश्न 6.
एक नगर में निर्वाह खर्च सूचकांक (cost of living index) का अध्ययन करने के लिए निम्नलिखित साप्ताहिक प्रेक्षण किए गए

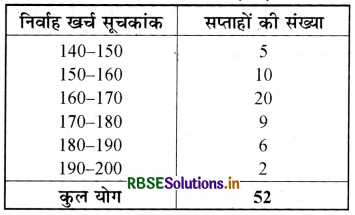
ऊपर दिए गए आँकड़ों का एक बारम्बारता बहुभुज (आयतचित्र बनाए बिना) खींचिए।
हल:
क्योंकि आयतचित्र बनाए बिना हम एक बारम्बारता बहुभुज खींचना चाहते हैं, इसलिए हम ऊपर दिए हुए वर्ग अन्तरालों, अर्थात् 140-150, 150-160, .... के वर्ग-चिह्न ज्ञात करेंगे। वर्ग अन्तराल 140-150 की ऊपरी सीमा = 150 और निम्न सीमा = 140 है।
अतः वर्ग-चिट = \(\frac{150+140}{2}=\frac{290}{2}\) = 145
इसी प्रकार, हम अन्य वर्ग अन्तरालों के वर्ग-चिह्न ज्ञात कर सकते हैं। इस प्रकार प्राप्त नई सारणी अग्रानुसार है-

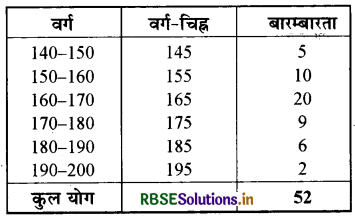
अब क्षैतिज अक्ष पर वर्ग-चिह्न आलेखित करके, ऊर्ध्वाधर अक्ष पर बारम्बारताएँ आलेखित करके और फिर बिन्दुओं B(145, 5),C(155, 10), D(165, 20), E(175, 9), F(185, 6) और G(195, 2) को आलेखित करके और उन्हें रेखाखण्डों से मिलाकर हम बारम्बारता बहुभुज खींच सकते हैं। हमें शून्य बारम्बारता के साथ वर्ग 130-140 (जो निम्नतम वर्ग 140-150 के ठीक पहले है) के वर्ग-चिह्न के संगत बिन्दु A(135, 0) को और G(195, 2) के तुरन्त बाद में आने वाले बिन्दु H(205, 0) को आलेखित करना भूलना नहीं चाहिए। इसलिए परिणामी बारम्बारता बहुभुज ABCDEFGH होगा (देखिए आकृति)।