RBSE Class 9 Maths Important Questions Chapter 13 Surface Areas and Volumes

Rajasthan Board RBSE Class 9 Maths Important Questions Chapter 13 Surface Areas and Volumes Important Questions and Answers.

RBSE Class 9 Maths Chapter 13 Important Questions Surface Areas and Volumes

I. Multiple Choice Questions:
Choose the correct answer from, the given options.

Question 1.
The length, breadth and height of cuboid are 15 cm, 12 cm and 4.5- cm respectively. Its volume is :
(a) 243 cm³
(b) 405 cm³
(c) 810 cm³
(d) 603 cm³
Answer:
(c) 810 cm³

Question 2.
How many bricks will be required to construct a wall 8 m long, 6 m high and 22.5 m thick if each brick measures (25 cm × 41.25 cm × 6 cm)?
(a) 4800
(b) 5600
(c) 6400
(d) 5200
Answer:
(c) 6400

Question 3.
If each side of a cube is doubled, then its volume :
(a) is doubled.
(b) becomes 4 times.
(c) becomes 6 times.
(d) becomes 8 times.
Answer:
(d) becomes 8 times.

Question 4.
The height Of a cylinder is 14 cm can its curved surface area is 264 cm2. The volume of the cylinder is :
(a) 308 cm³
(b) 396 cm³
(c) 1232 cm³
(d) 1848 cm³
Answer:
(b) 396 cm³

Question 5.
If each edge of cube is increased by 50%, then the percentage increase in its surface area is :
(a) 50%
(b) 75%
(c) 100%
(d) 125%
Answer:
(d) 125%

Question 6.
The ratio of the volume of a right circular cylinder and a right circular cone of the same base and the height will be :
(a) 1 : 3
(b) 3 : 1
(c) 4 : 3
(d) 3 : 4
Answer:
(b) 3:1

Question 7.
The lateral surface area of a cube is 256 m2. The volume of the cube is :
(a) 512 m³
(b) 64 m³
(c) 216 m³
(d) 256 m³
Answer:
(a) 512 m³

Question 8.
If the total surface area of cube is 96 cm2, then the volume of the cube is :
(a) 8 cm³
(b) 512 cm³
(c) 64 cm³
(d) 27 cm³
Answer:
(c) 64 cm³

Question 9.
The number of planks of dimensions (4 m × 50 cm × 20 cm) that can be stored in a pit which is 16 m long, 12 m wide and 4 m deep is :
(a) 1900
(b) 1920
(c) 1800
(d) 1840
Answer:
(b) 1920

Question 10.
In a cylinder, if radius is halved and height is double then the volume will be :
(a) same
(b) doubled
(c) halved
(d) four times
Answer:
(c) halved

Question 11.
In a cylinder, if radius is doubled and height is halved then its curved surface area will be :
(a) halved
(b) doubled
(c) same
(d) four times
Answer:
(c) same

Question 12.
If two cylinders of same lateral surface have their radii in the ratio 4 : 9, then the ratio of their heights is :
(a) 2:3
(b) 3 : 2
(c) 4 : 9
(d) 9 : 4
Answer:
(d) 9 : 4

Question 13.
If the radius of a sphere is 2n, then its volume will be :
(a) \(\frac{4}{3}\)πr³
(b) 4πr³
(c) \(\frac{8}{3}\)πr³
(d) \(\frac{32}{3}\)πr³
Answer:
(d) \(\frac{32}{3}\)πr³

Question 14.
The radius of a hemispherical balloon increases from 6 cm to 12 cm as air is being pumped into it. The ratio of the surface areas of the balloon in the two cases is :
(a) 1:4
(b) 1:3
(c) 2 : 3
(d) 2 : 1
Answer:
(a) 1:4

Question 15.
The total surface area of a cone whose radius is and slant height 2 l is :
(a) 2πr(l + r)
(b) πr(l + \(\frac{r}{4}\))
(c) πr(l + r)
(d) 2πrl
Answer:
(b) πr(l + \(\frac{r}{4}\))

II. Fill in the Blanks :

Question 1.
The total surface area of a cube is 96 cm². The volume of the cube is __________
Answer:
64 cm³

Question 2.
If the radius of the sphere is 2n, then its volume will be __________
Answer:
\(\frac{32}{3}\)πr³ cm³

Question 3.
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. Then the ratio of their curved surface areas, i.e. C₁: C₂ : C₃ = __________.
Answer:
\(\sqrt{h^{2}+r^{2}}\) : 2r : 2h

Question 4.
Surface area of sphere = __________.
Answer:
4πr²

Question 5.
Lateral surface area of a cuboid = __________.
Answer:
2(l + b)h sq. unit.

III. True/False :
State whether the following statements are True or False.

Question 1.
If the radius of a right circular cone is halved and height is doubled the volume will remain unchanged.
Answer:
False

Question 2.
The volume of a cone is equal to the volume of a cylider if they have same base and same height.
Answer:
False

Question 3.
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. The ratio of their volumes is 1 : 2 : 3.
Answer:
True

Question 4.
If a sphere is inscribed in a cube, then the ratio of the volume of the cube to the volume of the sphere will be 6 : n.
Answer:
True

Question 5.
The volume of a sphere is equal to two-thirds of the volume of a cylinder whose height and diameter are equal to the diameter of the sphere.
Answer:
True

Question 6.
The slant height of a cone is equal to the sum of square of its radius and height.
Answer:
False

Question 7.
The volume of a cone is equal to the volume of a cylinder if they have same base and same height.
Answer:
False

IV. Match the Columns :

Question 1.
Match the column I with the column II.

Column I	Column II
(1) Curved surface area of Cone	(i) 3πr2
(2) Curved surface of Hemisphere	(ii) 2πrh
(3) Curved surface area of Cylinder	(iii) 2πr2
(4) Total surface area of Hemisphere	(iv) πr2+ πr\(\sqrt{r^{2}+h^{2}}\)
(5) Total surface area of cone	(v) πr\(\sqrt{r^{2}+h^{2}}\)

Answer:

Column I	Column II
(1) Curved surface area of Cone	(v) πr\(\sqrt{r^{2}+h^{2}}\)
(2) Curved surface of Hemisphere	(iii) 2πr2
(3) Curved surface area of Cylinder	(ii) 2πrh
(4) Total surface area of Hemisphere	(i) 3πr2
(5) Total surface area of cone	(iv) πr2+ πr\(\sqrt{r^{2}+h^{2}}\)

V. Very Short Answer Type Questions :

Question 1.
What is the number of edges in a cube?
Answer:
12 edges.

Question 2.
The side of a cube is 1 cm. Find the total surface area of the figure obtained by joining two such cubes.
Answer:
When we join two cubes of side 1 cm each, we get a cuboid whose measurements are :
l = 1 + 1 = 2 cm, b = 1 cm, h = 1 cm.
∴ Total surface area = 2(lb + bh + hl) = 2[(2 × 1) + (1 × 1) + (1 × 2)]
= 2(2 + 1 + 2) = 2(5) = 10 cm².

Question 3.
The perimeter of the floor of a room is 30 m and its height is 4 m. Find the area of the four walls of the room.
Answer:
Perimeter of the floor = 2(l + b) = 30 m .
Also height = 4 m
∴ Area of 4 walls = 2(1 + b) × h = 30 × 4 = 120 cm².

Question 4.
The base radius and height of a cylinder are 7 cm and 14 cm respectively. Find its total surface area.
Answer':
Radius = r = 7 cm, Height = h = 14 cm
Total surface area of cylinder = 2πr(r + h)
= 2 × \(\frac{22}{7}\) × 7(7 + 14) = 44 × 21 = 924 cm².

Question 5.
The diameter of a sphere is d. Find its volume.
Answer:
Diameter of sphere = d
⇒ Radius of sphere = d/2
Volume of sphere = \(\frac{4}{3}\)π(radius)3 = \(\frac{4}{3}\)π × \(\left(\frac{d}{2}\right)^{3}\)
⇒ Volume = \(\frac{4}{3}\) × π × \(\frac{d^{3}}{8}=\frac{\pi d^{3}}{6}\)

VI. Short Answer Type Questions :

Question 1.
The dimensions of a cuboid are in the ratio of 1:2:3 and its total surface area is 88 m². Find the dimensions of the cuboid.
Answer:
Given, the dimensions of the cuboid are in the ratio 1 : 2
So, let the dimensions of cuboid be x m, 2x m and 3x m.
Then, total surface area = 2 (lb + bh + hl)
= 2(x × 2x + 2x × 3x + 3x × x)

But given surface area = 88 m²
2(x × 2x + 2x × 3x + 3x × x) = 88
⇒ 2(2x² + 6x² + 3x²) = 88
⇒ 2 × 11x² = 88
⇒ x² = \(\frac{88}{22}\) = 4
⇒ x = \(\sqrt{4}\) = 2 m
∴Dimensions of cuboid are : x = 2 m
2x = 2(2) = 4 m
and 3x = 3(2) = 6 m.

Question 2.
The length, breadth and height of a cuboid are 8 m, 6 m and 4 m respectively. Find its total surface area, diagonal and area of four walls.
Answer:
Given, length of cuboid (l) = 8 m, breadth (6) = 6 m and height (h) = 4 m
Total surface area of cuboid = 2(lb + bh + hl)
= 2(8 × 6 + 6 × 4 + 4 × 8) = 2(48 + 24 + 32) = 2 × 104 = 208 m²
Diagonal of cuboid = \(\sqrt{l^{2}+b^{2}+h^{2}}=\sqrt{(8)^{2}+(6)^{2}+(4)^{2}}\)
= \(\sqrt{64+36+16}=\sqrt{116}\) = 10.77 m
and area of the four walls of cuboid = 2(l + b)h = 2(8 + 6) × 4
= 2 × 14 × 4 = 112 m².

Question 3.
A solid cylinder has a total surface area of 231 m². Its curved surface area is \(\frac{2}{3}\) of the total surface area. Then, find the volume of the cylinder.
Answer:
Given : Total surface area of the cylinder = 231 cm²
Curved surface area = \(\frac{2}{3}\) × TSA = \(\frac{2}{3}\) × 231 = 154 m²
Now, \(\frac{\text { TSA of cylinder }}{\text { CSA of cylinder }}=\frac{231}{154}\)
⇒ \(\frac{\left(2 \pi r h+2 \pi r^{2}\right)}{(2 \pi r h)}=\frac{231}{154}=\frac{3}{2}\)
⇒ \(\frac{h+r}{h}=\frac{3}{2}\)
⇒ 2h + 2r = 3h
⇒ h = 2r .......(1)

As, Curved surface area = 2πrh = 154
⇒ 2πr(2r) = 154
⇒ 4πr² = 154
⇒ r² = \(\frac{154}{4} \times \frac{7}{22}=\frac{7 \times 7}{2 \times 2}\)
⇒ r = \(\frac{7}{2}\)
∴ h = 2 × \(\frac{7}{2}\) = 7 cm

Hence, required volume of cylinder = πr²h
= \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) × h = \(\frac{539}{2}\) = 269.50 m³

Question 4.
A cuboidal oil tin is 30 cm × 40 cm × 50 cm. Find the cost of the tin required for making 20 such tins, if the cost of tin sheet is ₹ 20 per sq m.
Answer:
Here, oil tin is in cuboidal form whose length (l) = 30 cm, breadth (b) = 40 cm and height (h) = 50 cm.
Surface area of one tin = l(lb + bh + hl)
= 2(30 × 40 + 40 × 50 + 30 × 50) = 2(1200 + 2000 + 1500)
= 2 × 4700 = 9400 cm²
Now, surface area of 20 such tins = 20 × 9400 = 188000 cm²
= \(\frac{188000}{10000}\) m² [∵ (100 cm)² = (1 m)² ⇒ 1 cm² = \(\frac{1}{10000}\) m²
= 18.8 m²

Given cost of 1 m² of tin sheet = ₹ 20
∴ Cost of 18.8 m² of tin sheet = ₹ 20 × 18.8 = ₹ 376
Hence, the cost of tin sheet for making 20 such tins is ₹ 376.

Question 5.
The water for a factory is stored in a hemispherical tank whose internal diameter is 14 m. The tank already contains 50 kilolitres of water. Water is pumped into the tank to fill its capacity. Calculate the volume of water
pumped into the tank. (Use π = \(\frac{22}{7}\))
Answer:
Hemispherical tank radius = \(\frac{14}{2}\) = 7m
Volume of hemisphere = \(\frac{2}{3}\) πr³
⇒ Volume of hemispherical tank = \(\frac{2}{3} \times \frac{22}{7}\) × (7)³ = \(\left(\frac{2156}{3}\right)\)m³

Now, volume of water already present in the tank = 50 kilolitres
= 50 m³ (∵ 1 kl = 1 m ³)

∴ Volume of water pumped into the tank = (\(\frac{2156}{3}\) - 50)
= \(\frac{2156-150}{3}=\left(\frac{2006}{3}\right)\) m³

Hence, the volume of water pumped into the tank is \(\left(\frac{2006}{3}\right)\) m³

Question 6.
A sphere and a cube have the same surface area. Show that the ratio of the volume of the sphere to that of the cube is √6 : √π.
Answer:
Let r be the radius of sphere and a be the length of an edge of a cube.
Surface area of sphere = 4πr²
Surface area of cube = 6a²
Surface area of sphere = Surface area of cube
4πr² = 6a²
\(\frac{4 \pi r^{2}}{6}\) = a²
a² = \(\frac{2 \pi r^{2}}{3}\) ∵ a = \(\frac{\sqrt{2} \pi r}{\sqrt{3}}\)

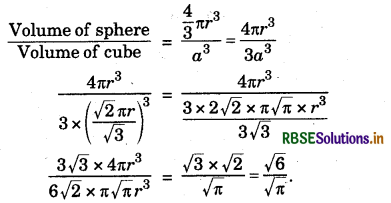
Question 7.
A sphere and a right circular cylinder of the same radius have equal volumes. By what percentage does the diameter of the cylinder exceed its height?
Answer:
Let r be radius and h be the height of cylinder.
Given : Radius of sphere = Radius of cylinder
Volume of cylinder = Volume of sphere
πr²h = \(\frac{4}{3}\)πr²
⇒ h = \(\frac{4 r}{3}=\frac{2}{3}\) × 2r = \(\frac{2 d}{3}\)
⇒ d = \(\frac{3}{2}\)h.

Difference of diameter and height of cylinder = d - h
= \(\frac{3}{2}\)h - h = \(\frac{h}{2}\)

∴ Percentage by which the diameter exceeds its height
= \(\frac{d-h}{h}\) × 100 = \(\frac{\frac{h}{2}}{h}\) × 100 = \(\frac{100}{2}\) = 50%
Hence, diameter exceeds the height by 50%.

Question 8.
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. Show that their volumes are in the ratio 1:2:3.
Answer:
Let 'r' be the radius of base and 'h' be the height of the solid.
As all the solids have equal heights
∴ h = r
Volume of cone V₁ = \(\frac{1}{3}\)πr²h = \(\frac{1}{3}\)πr³ (∵ h = r)

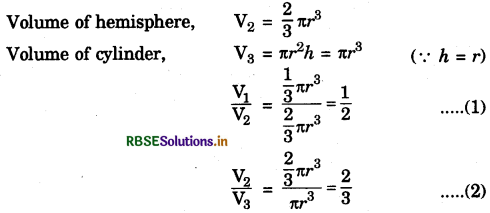
From (1) and (2), we get
V₁ : V₂ : V₃ = 1 : 2 : 3

Question 9.
A hemispherical tank full of water is emptied by a pipe at the rate of 3\(\frac{4}{7}\) litres per second. How much time will it take to empty half the tank, if it is 3 m in diameters? (Take π = \(\frac{22}{7}\))
Answer:
Diameter of tank = 3 m
∴ Radius of tank, r = \(\frac{3}{2}\)m

Volume of hemispherical tank = \(\frac{2}{3}\)πr³
= \(\frac{2}{3} \times \frac{22}{7} \times \frac{3}{2} \times \frac{3}{2} \times \frac{3}{2}=\frac{99}{14}\)m³ = \(\frac{99000}{14}\) litres

Volume of water to be emptied = \(\frac{1}{2} \times \frac{99000}{14}=\frac{99000}{28}\) litres
Rate of which water is emptied by a pipe
= 3\(\frac{4}{7}\) litres/s = \(\frac{25}{7}\) litres/s

Time required to empty half the tank = \(\frac{99000 / 28}{25 / 7}\)
= \(\frac{99000}{28} \times \frac{7}{25}\)
= 990 seconds = \(\frac{990}{60}\) mins = 16.5 mins

Question 10.
A boy has a spherical sweet of radius 4 cm. A girl has 8 spherical sweets each of radius 2 cm. Find the ratio of the volume of the sweets the boy has to the sweets the girl has.
Answer:
r₁ = 4 cm, r₂ = 2 cm
Let V₁ = Volume of sweet the boy has
V₂ = Volume of sweet the girl has

Then, V₁ = \(\frac{4}{3}\)π(r₁)³ and V₂ = [\(\frac{4}{3}\)π(r₂)³] × 8 (∵ Number of sweets = 8)
∴ \(\frac{V_{1}}{V_{2}}=\frac{\frac{4}{3} \pi\left(r_{1}\right)^{3}}{\frac{4}{3} \pi\left(r_{2}\right)^{3} \times 8}\)
⇒ \(\frac{V_{1}}{V_{2}}=\frac{(4)^{3}}{(2)^{3} \times 8}=\frac{(4)^{3}}{8 \times 8}=\frac{64}{64}\) = 1 : 1
∴ Ratio of volume of sweet of boy to the sweets of the girl is 1 : 1.

Question 11.
The radius of a sphere is 5 cm. If the radius is increased by 20% then find by how much percent volume is increased?
Answer:
Given, radius of the sphere (r₁) = 5 cm
New radius (r₂) = r₁ + 20% of r₁
= 5 + 20% of 5 = 5 + \(\frac{20 \times 5}{100}\) = 6 cm

∴ Volume of the sphere whose radius (r₁)
= \(\frac{4}{3}\)πr₁³ = \(\frac{4}{3}\) × π × (5)³ = \(\frac{4}{3}\) × π × 125

and volume of the sphere whose radius (r₂)
= \(\frac{4}{3}\)πr₂³ = \(\frac{4}{3}\) × π × (6)³ = \(\frac{4}{3}\) × π × 216

Difference in volumes = \(\frac{4}{3}\)πr₂³ - \(\frac{4}{3}\)πr₁³
= \(\frac{4}{3}\) × π × 125 - \(\frac{4}{3}\) × π × 216
= \(\frac{4}{3}\)π[216 - 125] = \(\frac{4}{3}\)π(91)

Now, percentage increase in volume
= \(\frac{\frac{4}{3} \pi(91)}{\frac{4}{3} \pi(125)}\) × 100 = \(\frac{364}{5}\) = 72.8%.

VII. Long Answer Type Questions :

Question 1.
A cylindrical water tank of diameter 1.4 m and height 2.1 m is being filled by a pipe of diameter 3.5 cm through which water flows at the rate of 2 m/s. Find the time taken in min by it to fill the tank.
Answer:
Given, diameter of the cylindrical water tank = 1.4 m
Radius of the cylindrical water tank = \(\frac{364}{5}\) = 70 cm (∵ 1 m = 100 cm)

Height of the cylindrical water tank = 2.1 m = 210 cm
∴ Volume of the cylindrical water tank = πr²h
= \(\frac{22}{7}\) × (70)₂ × 210 = 22 × 700 × 210 cm³

Radius of the pipe = \(\frac{3.5}{2}=\frac{7}{4}\) cm
Length of water which flows through the pipe in 1 s = 2 m = 200 cm (∵ 1 m = 100 cm)

∴ Volume of water delivered in 1 s through pipe
= Volume of a cylinder
= \(\frac{22}{7} \times\left(\frac{7}{4}\right)^{2}\) × (4) × 200 = 77 × 25 cm³
Hence, time taken to fill the cylindrical tank by the pipe
= \(\frac{22 \times 700 \times 210}{77 \times 25}\) = 1680 s = \(\frac{1680}{60}\) = 28 mm.

Question 2.
The diameter of a solid metallic right circular cylinder is equal to its height. After cutting out the largest possible solid sphere S from this cylinder, the remaining material is recast to form a solid sphere S₁ What is the ratio of the radius of sphere S to that of sphere S₁?
Answer:
Let the height of the cylinder be h.

Then, radius of the cylinder = \(\frac{h}{2}\)
Also, radius of the sphere (r) = \(\frac{h}{2}\)
∴ Volume of a cylinder = πr²h = π\(\left(\frac{h}{2}\right)^{2}\)h = \(\frac{\pi h^{3}}{4}\)
and volume of a sphere = \(\frac{4}{3}\)πr³ = \(\frac{4}{3}π\left(\frac{h}{2}\right)^{3} = \frac{\pi h^{3}}{6}\)
∴ Volume of the remaining material = \(\frac{\pi h^{3}}{4}-\frac{\pi h^{3}}{6}=\frac{\pi h^{3}}{12}\)

Now, volume of sphere recast from the remaining material,

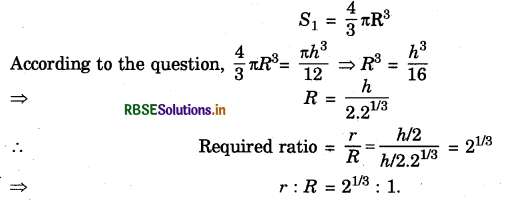
Question 3.
Surface area of a sphere of radius 5 cm is 5 times the area of the curved surface of a cone of radius 4 cm. Find the height of the cone.
Answer:
Radius of sphere, r = 5 cm
Radius of cone, r₁ = 4 cm
Let l and h be the slant height and height of the cone respectively.
SA of sphere = 5 × CSA of cone
4πr² = 5 × πr₁l
4r² = 5r₁ × l
4 × (5)² = 5r₁ × l
4 × (5)² = 5 × 4 × l
\(\frac{4 \times 25}{4 \times 5}\) = l ⇒ l = 5 cm
l² = r₁² + h ²
(5)² = (4)² + h²
⇒ 25 = 16 + h²
⇒ h² = 25 - 16 = 9
∴ h = 3 cm

Question 4.
The surface areas of two spheres are in the ratio 1 : 4. Find the ratio of their volumes.
Answer:

Question 5.
50 students of class X planned a visit to an old age home and to spend the whole day with its senior citizens. Each one prepared a cylindrical flower vase using cardboard to gift the senior citizens. The radius of cylinder is 4.2 cm and the height is 11.2 cm.
What is the amount spent for purchasing the cardboard at the rate of ₹ 20 per 100 m²?
Answer:
Given, radius of cylindrical vase (r) = 4.2 cm and height of the cylindrical flower vase (h) = 11.2 cm .
Surface area of cylindrical vase = Curved surface area of cylindrical flower vase + Area of vase = 2πrh + πr²
= 2π × 4.2 × 11.2 + π(4.2)²
= 4.2π(22.4 + 4.2) = 4.2 × \(\frac{22}{7}\) × 26.6
= 351.12 cm²

Now, surface area of 50 cylinders = 50 × 351.12 = 17556 cm²
So, total cost = 17556 × \(\frac{20}{100}\) × 100 = ₹ 351120.