RBSE Class 9 Maths Important Questions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन

Rajasthan Board RBSE Class 9 Maths Important Questions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Important Questions and Answers.

RBSE Class 9 Maths Chapter 13 Important Questions पृष्ठीय क्षेत्रफल एवं आयतन

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
एक घन का आयतन 343 सेमी. है। घन के एक पृष्ठ का क्षेत्रफल है
(A) 7 सेमी.²
(B) 14 सेमी.²
(C) 49 सेमी.²
(D) 249 सेमी.²
उत्तर:
(C) 49 सेमी.²

प्रश्न 2.
एक बेलन का वक्र पृष्ठ 528 सेमी. तथा ऊँचाई 14 सेमी. है। बेलन की त्रिज्या है
(A) 6 सेमी.
(B) 5 सेमी.
(C)4 सेमी.
(D) 3 सेमी.
उत्तर:
(A) 6 सेमी.

प्रश्न 3.
धातु के एक बेलन की त्रिज्या 2 सेमी. और ऊँचाई 7 सेमी. है। इसे पिघलाकर एक शंकु बनाया जाता है जिसकी त्रिज्या बेलन की त्रिज्या के समान है, तो उस शंकु की ऊँचाई है
(A) 28 सेमी.
(B) 21 सेमी.
(C) 14 सेमी.
(D) 7 सेमी.
उत्तर:
(B) 21 सेमी.

प्रश्न 4.
3080 घन सेमी. आयतन और 7 सेमी. त्रिज्या के बेलन की ऊँचाई है
(A) 10 सेमी.
(B) 15 सेमी.
(C) 20 सेमी.
(D) 25 सेमी.
उत्तर:
(C) 20 सेमी.

प्रश्न 5.
लकड़ी के एक बन्द सन्दूक की बाह्य लम्बाई, चौड़ाई व ऊँचाई क्रमशः 20 सेमी., 16 सेमी. तथा 12 सेमी. है। यदि लकड़ी की मोटाई 1 सेमी. हो, तो लकड़ी का आयतन होगा
(A) (20 × 16 × 12 - 18 × 14 × 10) सेमी.³
(B) (20 × 16 × 12 – 19 × 15 × 11) सेमी.³
(C) (22 × 18 × 14 - 20 × 16 × 12) सेमी.³
(D) (21 × 17 × 13 – 20 × 16 × 12) सेमी.³
उत्तर:
(A) (20 × 16 × 12 - 18 × 14 × 10) सेमी.³

प्रश्न 6.
8 मीटर भुजा वाली एक वर्गाकार दीवार में 40 सेमी. × 20 सेमी. वाली कितनी टाइल्स लगेंगी?
(A) 800
(B) 100
(C) 6400
(D) 51200
उत्तर:
(A) 800

प्रश्न 7.
एक आयताकार टंकी के पेंदे का क्षेत्रफल 20 वर्ग मीटर है। इस टंकी में 25 सेमी. ऊँचाई तक पानी भरा है। टंकी में पानी का आयतन होगा
(A) 20 × 25 घन मीटर
(B) 20 × \(\frac{1}{4}\) घन मीटर
(C) 20 × 20 × 25 घन मीटर
(D) 20 × 20 × \(\frac{1}{4}\) घन मीटर
उत्तर:
(B) 20 × \(\frac{1}{4}\) घन मीटर

प्रश्न 8.
यदि एक घन का सम्पूर्ण पृष्ठीय क्षेत्रफल 150 सेमी. है तो उसकी कोर है
(A) 4 सेमी.
(B) 5 सेमी.
(C) 16 सेमी.
(D) 25 सेमी.
उत्तर:
(B) 5 सेमी.

प्रश्न 9.
5 सेमी. त्रिज्या वाले अर्द्ध गोले का सम्पूर्ण पृष्ठ होगा
(A) 100π
(B) 75π
(C) 50π
(D) 25π
उत्तर:
(B) 75π

प्रश्न 10.
2 सेमी. त्रिज्या के एक बेलनाकार गिलास की ऊँचाई 8 सेमी. है तो उसमें भरे जा सकने वाले पानी का आयतन होगा
(A) \(\frac{108}{\pi}\) घन सेमी.
(B) 16 घन सेमी.
(C) 32 घन सेमी.
(D) 64 घन सेमी.
उत्तर:
(C) 32 घन सेमी.

प्रश्न 11.
यदि किसी घनाभ के तीन संलग्न पृष्ठों का क्षेत्रफल क्रमशः A₁, A₂ व A₃ है तब घनाभ का आयतन है
(A) A₁A₂A₃
(B) A₁A₂A₃
(C) \(\sqrt{A_{1} A_{2} A_{3}}\)
(D) \(\sqrt[3]{\mathrm{A}_{1} \mathrm{~A}_{2} \mathrm{~A}_{3}}\)
उत्तर:
(C) \(\sqrt{A_{1} A_{2} A_{3}}\)

प्रश्न 12.
यदि किसी धनाभ की तीनों भुजाएँ x, y, 2 हैं तथा इसका आयतन V और पृष्ठीय क्षेत्रफल A है, तब \(\frac{\mathrm{A}}{\mathrm{V}}\) होगा
(A) x²y²z²
(B) \(\frac{1}{2}\left(\frac{1}{x y}+\frac{1}{y z}+\frac{1}{z x}\right)\)
(C) \(\frac{1}{2}\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\)
(D) \(\frac{1}{x y z}\)
उत्तर:
(C) \(\frac{1}{2}\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\)

प्रश्न 13.
यदि किसी तार की त्रिज्या को घटाकर एक तिहाई कर दिया जाए, तब इसकी लम्बाई होगी, जबकि उसका आयतन अपरिवर्तित रहे
(A) 3 गुना
(B) 6 गुना
(C) 9 गुना
(D) 27 गुना
उत्तर:
(C) 9 गुना

प्रश्न 14.
दो बेलनों का आयतन समान है जबकि उनकी ऊँचाई का अनुपात 1 : 2 है। तब उनकी त्रिज्याओं का अनुपात है
(A) 1: √2
(B) √2:1
(C) 1 : 2
(D) 1 : 4
उत्तर:
(B) √2:1

प्रश्न 15.
यदि किसी शंकु की त्रिज्या 2r तथा तिर्यक ऊँचाई \(\frac{l}{2}\) है, तब उसका वक्र पृष्ठीय क्षेत्रफल है
(A) πrl
(B) 2πrl
(C) \(\frac{1}{2}\)πrl
(D) π(r + l)r
उत्तर:
(B) 2πrl
प्रश्न 16.
यदि दो शंकुओं की ऊँचाई का अनुपात 1 : 4 है, उनके आधार की त्रिज्याओं का अनुपात 4 : 1 है तब उनके आयतनों का अनुपात होगा
(A) 1 : 2
(B) 2 : 3
(C) 3 : 4
(D) 4 : 1
उत्तर:
(D) 4 : 1

प्रश्न 17.
यदि h. S व V किसी लम्ब वृत्तीय शंकु की क्रमशः ऊँचाई, वक्र पृष्ठीय क्षेत्रफल और आयतन हों तो 3πVh³ - S² + 9V² बराबर है
(A) 8
(B) 0
(C) 4π
(D) 32π²
उत्तर:
(B) 0

प्रश्न 18.
समान त्रिज्या के गोले और अर्द्धगोले के पृष्ठीय क्षेत्रफलों का अनुपात है
(A) 2 : 1
(B) 3 : 2
(C) 4 : 3
(D) 4 : 1
उत्तर:
(C) 4 : 3

प्रश्न 19.
यदि एक गोला एवं घन समान ऊँचाई के हैं। उनके आयतनों का अनुपात है
(A) 3 : 4
(B) 21 : 11
(C) 4 : 3
(D) 11 : 21
उत्तर:
(D) 11 : 21

प्रश्न 20.
यदि एक शंकु और अर्द्धगोले का आधार और आयतन समान है तब इनकी ऊँचाई का अनुपात है
(A) 1 : 2
(B) 2 : 1
(C) 4 : 1
(D) √2 : 1.
उत्तर:
(A) 1 : 2

प्रश्न 21.
यदि किसी गोले का पृष्ठीय क्षेत्रफल 1447 मी.² है तब इसका आयतन है
(A) 3167 मी.³
(B) 2887 मी.³
(C) 1887 मी.³
(D) 3007 मी.³
उत्तर:
(B) 2887 मी.³

प्रश्न 22.
किसी गोले एवं उसके अन्दर बने सबसे बड़े लम्ब वृत्तीय बेलन के आयतन का अनुपात है
(A) 2 : 1
(B) 1 : 1
(C) 2 : 3
(D) 1 : 2
उत्तर:
(C) 2 : 3

प्रश्न 23.
यदि दो गोलों के आयतनों का अनुपात 1 : 8 है, तब उनके पृष्ठीय क्षेत्रफलों का अनुपात है
(A) 1 : 4
(B) 1 : 2
(C) 1 : 8
(D) 1 : 16
उत्तर:
(A) 1 : 4

प्रश्न 24.
यदि एक शंकु, एक अर्द्धगोला एवं एक बेलन समान आधार पर हैं और उनकी ऊँचाई समान है, तब उनके आयतनों का अनुपात है
(A) 1 : 2 : 3
(B) 2 : 1 : 3
(C) 2 : 3 : 1
(D) 3 : 2 : 1
उत्तर:
(A) 1 : 2 : 3

प्रश्न 25.
यदि किसी घन के सभी किनारों की लम्बाइयों का योग 36 सेमी. है, तब घन का आयतन (सेमी.) में है
(A) 9
(B) 27
(C) 219
(D) 729
उत्तर:
(B) 27

रिक्त स्थानों की पूर्ति करो

प्रश्न 1.
घनाभ के दो आसन्न फलक एक रेखाखण्ड पर मिलते हैं, जिसे _______ कहते हैं।
उत्तर:
कोर

प्रश्न 2.
जब घनाभ की लम्बाई, चौड़ाई और ऊँचाई समान हो तो उसे __________ कहते हैं।
उत्तर:
घन

प्रश्न 3.
घन का सम्पूर्ण पृष्ठीय क्षेत्रफल __________
उत्तर:
6(भुजा)²

प्रश्न 4.
1 लीटर = __________ घन सेमी.
उत्तर:
1000

प्रश्न 5.
1 घनमीटर = __________ किलोलीटर
उत्तर:
1

प्रश्न 6.
बेलन का सम्पूर्ण पृष्ठ क्षेत्रफल = __________ + 2 × __________
उत्तर:
वक्र पृष्ठ, आधार का क्षेत्रफल

प्रश्न 7.
गोले की त्रिज्या r हो तो गोले का पृष्ठीय क्षेत्रफल __________
उत्तर:
4πr² वर्ग इकाई

प्रश्न 8.
यदि किसी घनाभ के तीन संलग्न पृष्ठों के क्षेत्रफल क्रमशः A₁, A₂ व A₃ हैं तब घनाभ का आयतन = __________
उत्तर:
\(\sqrt{\mathrm{A}_{1} \mathrm{~A}_{2} \mathrm{~A}_{3}}\)

प्रश्न 9.
यदि किसी घनाभ की तीनों भुजाएँ x, y, z हैं तथा इसका आयतन V और पृष्ठीय क्षेत्रफल A है तब \(\frac{\mathrm{A}}{\mathrm{V}}\) का मान __________ होगा।
उत्तर:
\(\frac{1}{2}\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\)

प्रश्न 10.
यदि किसी तार की त्रिज्या को घटाकर एक तिहाई कर दिया जाए, तब इसकी लम्बाई __________ गुना होगी जबकि इसका आयतन अपरिवर्तित रहे।
उत्तर:
9 गुना

सत्य/असत्य-निम्नलिखित कथनों के लिए सत्य अथवा असत्य लिखिए

प्रश्न 1.
घनाभ का सम्पूर्ण पृष्ठीय क्षेत्रफल = 2 (ल. × चौ. + चौ. × ॐ. + ऊँ. × ल.) वर्ग इकाई
उत्तर:
सत्य

प्रश्न 2.
r त्रिज्या व h ऊँचाई वाले शंकु का आयतन \(\frac{2}{3}\)πr²h होता है।
उत्तर:
असत्य

प्रश्न 3.
r त्रिज्या वाले अर्द्धगोले के सम्पूर्ण पृष्ठ का क्षेत्रफल = 3πr² होता है।
उत्तर:
सत्य

प्रश्न 4.
दो बेलनों का आयतन समान है जबकि उसकी ऊँचाई का अनुपात 1 : √2 है। तब उनकी त्रिज्याओं का अनुपात √2 : 1 है।
उत्तर:
सत्य

प्रश्न 5.
यदि किसी शंकु की त्रिज्या 25 तथा तिर्यक ऊँचाई l/2 है, तब उसका वक्र पृष्ठीय क्षेत्रफल 4πrl होगा।
उत्तर:
असत्य

प्रश्न 6.
समान त्रिज्या के गोले और अर्द्धगोले के पृष्ठीय क्षेत्रफलों का अनुपात 4 : 3 होता है।
उत्तर:
सत्य

प्रश्न 7.
यदि एक गोला एवं घन समान ऊँचाई के हैं। उनके आयतनों का अनुपात 12 : 21 होगा।
उत्तर:
असत्य

8. यदि किसी गोले का पृष्ठीय क्षेत्रफल 144π मी.² है तब उसका आयतन 188 π मी³. होगा।
उत्तर:
सत्य

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
यदि एक घन का सम्पूर्ण पृष्ठीय क्षेत्रफल 384 सेमी.2 है, तो घन के एक तल का क्षेत्रफल लिखिए।
हल:
(भुजा)² = घन के एक तल का क्षेत्रफल
= \(\frac{384}{6}\) = 64 सेमी.²

प्रश्न 2.
यदि एक बेलन के वक्र पृष्ठ का क्षेत्रफल 1760 सेमी. तथा त्रिज्या 14 सेमी. है, तो उसकी ऊँचाई लिखिए।
हल:
ऊंचाई = \(\frac{1760}{2 \pi \times 14}\)
= \(\frac{1760 \times 7}{2 \times 22 \times 14}\) = 20 सेमी.

प्रश्न 3.
एक लम्बवृत्तीय शंकु के आधार की त्रिज्या 6 सेमी. तथा ढालू ऊँचाई 28 सेमी. है। शंकु के वक्रपृष्ठ का क्षेत्रफल लिखिए।
हल:
शंकु के वक्रपृष्ठ का क्षेत्रफल
= πrl = π × 6 × 28
= \(\frac{22}{7}\) × 6 × 28 = 528 सेमी.

प्रश्न 4.
एक डिब्बे की लम्बाई उसकी चौड़ाई की दुगुनी है। यदि उसकी लम्बाई 16 सेमी. तथा ऊँचाई 6 सेमी. हो तो डिब्बे का सम्पूर्ण पृष्ठीय क्षेत्रफल लिखिए।
हल:
यहाँ लम्बाई = 16 सेमी.
अतः चौड़ाई = 8 सेमी.

सम्पूर्ण पृष्ठीय क्षेत्रफल
= 2 (16 × 8 + 8 × 6 + 16 × 6)
= 2 (128 + 48 + 96)
= 2 (272) = 544 सेमी.

प्रश्न 5.
एक घनाकार डिब्बे का आयतन 64 घन सेमी. है। डिब्बे की प्रत्येक कोर (भुजा) की नाप लिखिए।
हल:
भुजा = \(\sqrt[3]{64}\) = (4³)^1/3 = 4 सेमी.

प्रश्न 6.
पानी की एक टंकी की माप 1 मीटर × 80 सेमी. × 50 सेमी. है। टंकी कितने लीटर पानी से पूरी भर जाएगी?
हल:
टंकी का आयतन = \(\frac{100 \times 80 \times 50}{1000}\)
= 400 लीटर

प्रश्न 7.
एक घन का सम्पूर्ण पृष्ठीय क्षेत्रफल 150 वर्ग मीटर है। उसकी कोर (भुजा) की लम्बाई लिखिए।
हल:
6 (भुजा)² = 150
भुजा = \(\sqrt{\frac{150}{6}}\) = 5 मीटर

प्रश्न 8.
किसी शंकु की ढालू (तिर्यक) लम्बाई 5 सेमी. तथा ऊँचाई 4 सेमी. है, तो उसका व्यास लिखिए।
हल:
= \(\sqrt{5^{2}-4^{2}}=\sqrt{25-16}\)
= √9 = 3
अतः व्यास = 2 × 3 = 6 सेमी.

प्रश्न 9.
एक बेलन का आयतन 108π सेमी. है। यदि उसकी ऊँचाई 12 सेमी. हो तो बेलन की त्रिज्या लिखिए।
हल:
πr²h = 108π
r² = \(\frac{108 \pi}{\pi \times 12}\) = 9
अतः r = 3 सेमी.

प्रश्न 10.
एक बेलन का वक्रपृष्ठ 147 cm तथा त्रिज्या 7 सेमी. है तो ऊँचाई ज्ञात कीजिए।
हल:
2πrh = 14π
अत: rh = 7 व
h = \(\frac{7}{7}\) = 1 सेमी.

प्रश्न 11.
एक शंक्वाकार ठोस की त्रिज्या 7 सेमी., ढालू लम्बाई 25 सेमी. तथा ऊँचाई 24 सेमी. है। ठोस का आयतन लिखिए।
हल:
आयतन = \(\frac{1}{3} \times \frac{22}{7}\) × 7 × 7 × 24
= 1232 घन सेमी.

प्रश्न 12.
एक शंकु का आयतन 132 घन मीटर है। यदि शंकु की ऊँचाई 14 मीटर हो तो शंकु की त्रिज्या लिखिए।
हल:
r² = \(\frac{132 \times 7 \times 3}{22 \times 14}\)
r = \(\sqrt{3 \times 3}\) = 3 मीटर

प्रश्न 13.
एक ठोस गोले का व्यास 6 सेमी. है। गोले का आयतन लिखिए। (उत्तर π में दीजिए।)
हल:
आयतन = \(\frac{4}{3}\)πr³
= \(\frac{4}{3}\) × π × 3 × 3 × 3
= 36π घन सेमी.

प्रश्न 14.
एक गोले का पृष्ठीय क्षेत्रफल 100π वर्ग मीटर है। उसकी त्रिज्या लिखिए।
हल:

प्रश्न 15.
यदि दो गोलों की त्रिज्याओं का अनुपात 2 : 3 है, तो उनके आयतन का अनुपात लिखिये।
हल:
पहले गोले का आयतन
V₁ = \(\frac{4}{3}\)r₁³

इसी तरह से दूसरे गोले का आयतन

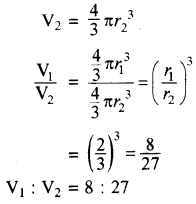
लघूत्तरात्मक प्रश्न

प्रश्न 1.
एक ढक्कनदार सन्दक 2 सेमी. मोटी लकड़ी का बना है। सन्दूक की बाहर से लम्बाई, चौड़ाई और ऊँचाई क्रमशः 94 सेमी., 64 सेमी. और 44 सेमी. है। सन्दूक के अन्दर का आयतन ज्ञात कीजिए।
हल:
सन्दूक की बाहरी लम्बाई = 94 सेमी.
सन्दूक की बाहरी चौड़ाई = 64 सेमी.
सन्दूक की बाहरी ऊँचाई = 44 सेमी.
सन्दूक की मोटाई = 2 सेमी.

∴ सन्दूक की आन्तरिक लम्बाई = (94 - 4)
= 90 सेमी.

∴ सन्दूक की आन्तरिक चौड़ाई = (64 - 4)
= 60 सेमी.

∴ सन्दूक की आन्तरिक ऊँचाई = (44 - 4)
= 40 सेमी.

सन्दूक के अन्दर का आयतन
= 90 × 60 × 40 घन सेमी.
= 216000 घन सेमी.

प्रश्न 2.
सीसे के एक घनाभ का माप 5 सेमी. × 10 सेमी. × 15 सेमी. है। इसे पिघलाकर 5 सेमी. भुजा के कितने घन बनाए जा सकते हैं ?
हल:
सीसे के एक धनाभ का माप
= 5 सेमी. × 10 सेमी. × 15 सेमी. घनाभ का आयतन होगा।
= 5 × 10 × 15 घन सेमी.
= 750

घन सेमी. घन की भुजा = 5 सेमी.
घन का आयतन = (भुजा) घन इकाई
= (5)3

घन सेमी. = 5 × 5 × 5 घन सेमी.
= 125 घन सेमी.

∴ 125 घन सेमी. से बनता है = 1 घन
1 घन सेमी. से बनेगा = 3 घन

∴ 750 घन सेमी. से बनेंगे = 5 × 750
= 6 घन

∴ 6 घन बनाए जा सकेंगे।

प्रश्न 3.
मैरी अपने क्रिसमस वृक्ष को सजाना चाहती है। वह इस वृक्ष को लकड़ी के एक घनाभाकार बॉक्स (box) पर रखना चाहती है, जिसे सान्ता क्लॉज के चित्र के साथ एक रंगीन कागज से ढका जाना है ( देखिए आकृति)। उसका यह जानना आवश्यक है कि उसे कितना कागज खरीदना चाहिए। यदि दिये गये बॉक्स की लम्बाई, चौड़ाई और ऊँचाई क्रमशः 80 cm, 40 cm और 20 cm है, .तो उसे 40 cm भुजा वाली कागज की कितनी वर्गाकार शीटों की आवश्यकता होगी?
हल:
चूँकि मैरी बॉक्स के ऊपरी पृष्ठ को कागज से ढकना चाहती है, इसलिए इस कार्य के लिए आवश्यक कागज इस बॉक्स के पृष्ठीय क्षेत्रफल के बराबर होगा, जो एक घनाभ के आकार का है।
बॉक्स की लम्बाई 80 cm, चौड़ाई 40 cm और ऊँचाई 20 cm है।
अतः बॉक्स का पृष्ठीय क्षेत्रफल = 2(lb + bh + hl)
= 2[(80 × 40) + (40 x× 20) + (20 × 80)] cm
= 2[3200 + 800 + 1600] cm
= 2 × 5600 cm²
= 11200 cm²

अब, प्रत्येक शीट का क्षेत्रफल
= 40 × 40 cm²
= 1600 cm

अतः वांछित शीटों की संख्या बॉक्स का पृष्ठीय क्षेत्रफल एक शीट का क्षेत्रफल

इसलिए मैरी को कागज की 7 शीटों की आवश्यकता है।

प्रश्न 4.
हमीद ने अपने घर के लिए, ढक्कन वाली एक घनाकार (cubical) पानी की टंकी बनवाई है, जिसका प्रत्येक बाहरी किनारा 1.5 m लम्बा है। वह इस टंकी के बाहरी पृष्ठ पर, तली को छोड़ते हुए, 25 cm भुजा वाली वर्गाकार टाइलें (tiles) लगवाता है ( देखिए आकृति)। यदि टाइलों की लागत 360 रुपये प्रति दर्जन है, तो उसे टाइल लगवाने में कितना व्यय करना पड़ेगा?

हल:
हमीद पाँच बाहरी फलकों पर टाइलें लगवाता है। टाइलों की संख्या ज्ञात करने के लिए इन पाँचों फलकों का क्षेत्रफल ज्ञात करना आवश्यक है। अब, घनाकार टंकी का एक किनारा
= 1.5 m = 150 cm

अतः टंकी का पृष्ठीय क्षेत्रफल
= 5 × 150 × 150 cm

एक टाइल का क्षेत्रफल
= भुजा - भुजा = 25 × 25 cm

अतः टाइलों की वांछित संख्या

अब 1 दर्जन, अर्थात् 12 टाइलों की लागत
= 360 रुपये

इसलिए, 1 टाइल की लागत
= \(\frac{360}{12}\) रुपये = 30 रुपये

अतः 180 टाइलों की लागत = 180 × 30 रुपये
= 5400 रुपये

प्रश्न 5.
सावित्री को अपने विज्ञान के प्रोजेक्ट के लिए एक बेलनाकार केलिडोस्कोप (kaleidoscope) का मॉडल बनाना था। वह इस केलिडोस्कोप की वक्र पृष्ठ बनाने के लिए चार्ट कागज (chart paper) का प्रयोग करना चाहती थी ( देखिए आकृति)। यदि वह 25 cm लम्बाई और 3.5 cm त्रिज्या का केलिडोस्कोप बनाना चाहती है, तो उसे चार्ट कागज के कितने क्षेत्रफल की आवश्यकता होगी? (r = 22 लीजिए)

हल:
बेलनाकार केलिडोस्कोप की त्रिज्या
(r) = 3.5 cm

केलिडोस्कोप की ऊँचाई (लम्बाई)
(h) = 25 cm

अतः आवश्यक चार्ट कागज का क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh.
= 2 × \(\frac{22}{7}\) × 3.5 × 25 cm
= 550 cm

प्रश्न 6.
एक खुले मैदान में 10 m लम्बी एक दीवार का निर्माण किया जाना था। दीवार की ऊँचाई 4m है और उसकी मोटाई 24 cm है। यदि इस दीवार को 24 cm x 12 cm x 8 cm विमाओं वाली ईंटों से बनाया जाना है, तो इसके लिए कितनी ईंटों की आवश्यकता होगी?
हल:
चूँकि दीवार द्वारा घेरा गया स्थान सभी ईंटों द्वारा घेरे गये स्थान के बराबर होगा, इसलिए आइए दीवार का आयतन ज्ञात करें, जो एक घनाभ है।
यहाँ लम्बाई = 10 m = 1000 cm,
मोटाई = 24 cm और ऊँचाई = 4 m = 400 cm

अतः दीवार का आयतन.
= लम्बाई × मोटाई × ऊँचाई
= 1000 × 24 × 400 cm

अब प्रत्येक ईंट विमाओं 24 cm × 12 cm × 8 cm का एक घनाभ है।
इसलिए, एक ईंट का आयतन = लम्बाई × चौड़ाई × ऊँचाई
= 24 × 12 × 8 cms

अत: वांछित ईंटों की संख्या

इसलिए, दीवार बनाने में 4167 ईंटें लगेंगी।

प्रश्न 7.
एक शंकु के आधार की त्रिज्या 7 सेमी. तथा ऊँचाई 24 सेमी. है। शंकु का वक्रपृष्ठ ज्ञात कीजिए।
हल:
शंकु का वक्रपृष्ठ = πrl
यहाँ r = 7 सेमी. व h = 24 सेमी. है।

प्रश्न 8.
एक लम्बवृत्तीय शंकु की ऊँचाई 12 सेमी. तथा आधार की त्रिज्या 3.5 सेमी. है। उसके वक्रपृष्ठ का क्षेत्रफल ज्ञात कीजिए।
हल:
शंकु की ऊँचाई l = 12 सेमी.
शंकु की त्रिज्या r = 3.5 सेमी.

शंकु की तिरछी ऊँचाई l = \(\sqrt{r^{2}+h^{2}}\)
= \(\sqrt{(3.5)^{2}+(12)^{2}}\)
= \(\sqrt{12.25+144}\)
= \(\sqrt{156.25}\)
l = 12.5 सेमी.

शंकु के वक्रपृष्ठ का क्षेत्रफल = πrl
= \(\frac{22}{7}\) × 3.5 × 12.5 सेमी.²
= 11 × 12.5 सेमी.²
= 137.5 सेमी.²

प्रश्न 9.
एक शंकु का आयतन 308 सेमी.' और ऊँचाई 6 सेमी. है। उसके आधार की त्रिज्या ज्ञात कीजिए।
हल:
शंकु का आयतन = \(\frac{1}{3}\)πr²h = 308 सेमी³
⇒ r² = \(\frac{308 \times 3}{\pi \times h}\)
⇒ r² = \(\frac{308 \times 3 \times 7}{22 \times 6}\)
r² = 49
r = \(\sqrt{49}\)
शंकु के आधार की त्रिज्या = 7 सेमी.

प्रश्न 10.
शंकु, अर्द्ध गोला और एक बेलन समान वृत्ताकार आधार और समान ऊँचाई के हैं। इनके आयतनों का अनुपात ज्ञात कीजिए।
हल:
एक शंकु, एक अर्द्ध गोला और एक बेलन एक ही आधार और ऊँचाई पर बने हैं।
∴ आधार तथा ऊँचाई को x मानने पर
एक शंकु का आयतन होगा = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3}\)πx³

एक अर्द्ध गोले का आयतन होगा = \(\frac{2}{3}\)πr³
= \(\frac{2}{3}\)πr³

एक बेलन का आयतन होगा = πr²h = πx³

तीनों के आयतन का अनुपात होगा
= शंकु : अर्द्ध गोला : बेलन
= \(\frac{1}{3}\)πx³ : \(\frac{2}{3}\)πr³ : πx³
= πx³(\(\frac{1}{3}\) : \(\frac{2}{3}\) : 3)
अतः तीनों के आयतन का क्रमशः अनुपात होगा 1 : 2 : 3

प्रश्न 11.
एक भुट्टा कुछ-कुछ शंकु जैसे आकार का है ( देखिए आकृति) जिसके सबसे चौड़े सिरे की त्रिज्या 2.1 cm है और इसकी लम्बाई (ऊँचाई) 20 cm है। यदि भुट्टे के प्रत्येक 1 cm² पृष्ठ पर औसतन चार दाने हों, तो ज्ञात कीजिए कि पूरे भुट्टे पर कुल कितने दाने होंगे?

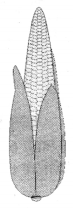
हल:
चूँकि भुट्टे के दाने उसके वक्र पृष्ठ पर ही होते हैं, इसलिए हमें दानों की संख्या ज्ञात करने के लिए भुट्टे के वक्र पृष्ठीय क्षेत्रफल को ज्ञात करना होगा। यहाँ हमें शंकु की ऊँचाई दी है। इसलिए, हमें पहले शंकु की तिर्यक ऊँचाई ज्ञात करनी पड़ेगी।
अब l = \(\sqrt{r^{2}+h^{2}}=\sqrt{(2.1)^{2}+20^{2}}\) cm
= \(\sqrt{404.41}\) cm = 20.11 cm

अतः भुट्टे का वक्र पृष्ठीय क्षेत्रफल = πrl
= \(\frac{22}{7}\) × 2.1 × 20.11 cm
= 132.726 cm²
= 132.73 cm² (लगभग)
अत: 1 cm² क्षेत्रफल पर दानों की संख्या = 4

इसलिए, पूरे भुट्टे पर कुल दानों की संख्या
= 132.73x4
= 530.92 = 531 (लगभग)
अतः इस भुट्टे पर लगभग 531 दाने होंगे।

प्रश्न 12.
यदि एक गोले का पृष्ठीय क्षेत्रफल 616 सेमी. है, तो उसका आयतन ज्ञात कीजिए।
हल:
माना कि गोले की त्रिज्या r है। अत:
गोले का पृष्ठीय क्षेत्रफल = 4πr² = 616
या 4 × \(\frac{22}{7}\) × r² = 616
या r² = \(\frac{616 \times 7}{4 \times 22}\)
या r² = 49
या r = 7 सेमी.

गोले का आयतन = \(\frac{4}{3}\)πr³
= \(\frac{4}{3} \times \frac{22}{7}\) × 7 × 7 × 7 सेमी.³
= 1437.33 सेमी.³

प्रश्न 13.
सर्कस का एक मोटर साइकिल सवार जिस खोखले गोले के अन्दर अपने करतब (खेल) दिखाता है, उसका व्यास 7 m है। मोटर साइकिल सवार के पास ये करतब दिखाने के लिये कितना क्षेत्रफल उपलब्ध है?
हल:
गोले का व्यास = 7 m है।
इसलिए इसकी त्रिज्या = \(\frac{7}{2}\) = 3.5 मी.
अब करतब दिखाने के लिए मोटर साइकिल सवार को उपलब्ध स्थान इस गोले का पृष्ठीय क्षेत्रफल होगा।
अतः गोले का पृष्ठीय क्षेत्रफल = 4πr²
= 4 × \(\frac{22}{7}\) × 3.5 × 3.5
= 4 × 22 × 0.5 × 3.5
= 154 m²

निबन्धात्मक प्रश्न

प्रश्न 1.
48 सेमी. × 36 सेमी. माप की एक धातु | की आयताकार चद्दर है। इसके प्रत्येक कोने से 8 सेमी. भुजा का वर्ग काटकर निकाल दिया गया है। शेष चद्दर से ऊपर से खुला एक सन्दूक बनाया गया है। सन्दूक का आयतन ज्ञात कीजिए।
हल:
धातु के आयताकार चद्दर की लम्बाई = 48 सेमी.
धातु के आयताकार चद्दर की चौड़ाई = 36 सेमी.
∵ धातु की आयताकार चद्दर के प्रत्येक कोने से 8 सेमी. भुजा का वर्ग काट दिया है और शेष चद्दर से ऊपर से खुला हुआ एक सन्दूक बनाया गया है अतः
सन्दूक की लम्बाई = 48 - 16 = 32 सेमी.
सन्दूक की चौड़ाई = 36 - 16 = 20 सेमी.
तथा सन्दूक की ऊँचाई = काटे गए. वर्ग की भुजा = 8 सेमी.

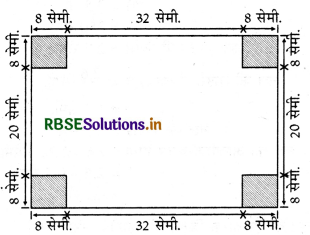
सन्दूक का आयतन = ल. × चौ. × ऊँ.
= 32 × 20 × 8 सेमी.³
= 5120 सेमी.³

प्रश्न 2.
एक घनाभ के तीन आसन्न फलकों का क्षेत्रफल क्रमशः x, y तथा है। सिद्ध कीजिये कि घनाभ का आयतन √xyz है।
हल:
माना घनाभ की लम्बाई, चौड़ाई और ऊँचाई क्रमशः l, b और h हैं।
प्रश्नानुसार l × b = x .....(i)
b × h .....(ii)
और, h × l = z ....(iii)
समीकरण (i), (ii) और (iii) का गुणा करने पर
l × b × b × h × h × l = x × y × z
l² b² h² = xyz.
(lbh) = xyz
lbh = √xyz
घनाभ का आयतन = √xyz इतिसिद्धम्

प्रश्न 3.
काँच के एक बेलनाकार जार में 5390 सेमी. पानी भरा जा सकता है। यदि इसकी भीतरी ऊँचाई 35 सेमी. है, तो जार की त्रिज्या ज्ञात कीजिए।
हल:
बेलनाकार जार का आयतन (πr²h)
= 5390 सेमी.²
बेलनाकार जार की ऊँचाई = 35 सेमी.

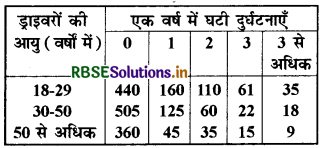
= \(\sqrt{\frac{5390}{110}}\) सेमी. = √49 सेमी.
= 7 सेमी.

प्रश्न 4.
एक आयताकार कागज की शीट की लम्बाई 44 सेमी. और चौड़ाई 18 सेमी. है। इसे लम्बाई की ओर से मोड़कर एक बेलन इस प्रकार बनाया जाता है कि सम्मुख भुजाएँ एक-दूसरे को स्पर्श करें। इस प्रकार बने बेलन का आयतन ज्ञात कीजिए।
हल:
आयताकार कागज की शीट की लम्बाई को . मोड़ने से एक बेलन प्राप्त होगा जिसके आधार की परिधि कागज की लम्बाई के बराबर होगी।
∵ बेलन के आधार की परिधि = कागज की लम्बाई
2πr = 44 सेमी.
∵ त्रिज्या (r) = \(\frac{44}{2 \pi}=\frac{22}{\pi}\) = 22 × \(\frac{7}{22}\) सेमी.
= 7 सेमी.
∵ कागज की चौड़ाई = कागज से बने बेलन की ऊँचाई
∴ बेलन का आयतन = πr²h
= \(\frac{22}{7}\) × 7 × 7 × 18 सेमी.³
= 2772 सेमी.³

प्रश्न 5.
एक 21 मीटर गहरा और 6 मीटर व्यास वाला कुआं बनाने के लिए कितने घन मीटर मिट्टी खोदनी पड़ेगी? यह भी ज्ञात कीजिए कि कुएं की आन्तरिक सतह को 95 रुपये प्रति वर्ग मीटर की दर से प्लास्टर करवाने का खर्च क्या होगा?
हल:
चूँकि कुआं बेलनाकार आकृति का है, इसलिए इसकी गहराई ही ऊँचाई है।
अतः कुएं की गहराई (ऊँचाई) = 21 मीटर
कुएं की त्रिज्या = \(\frac{6}{2}\) मीटर
= 3 मीटर
कुएं का आयतन या घन मीटर मिट्टी होगी
= πr²h
= \(\frac{22}{7}\) × 3 × 3 × 21
= 22 × 3 × 3 × 3 मीटर³
= 594 मीटर³
∵ प्लास्टर कुएं के आन्तरिक पृष्ठ भाग में होगा
∴ कुएं के आन्तरिक पृष्ठ भाग का क्षेत्रफल होगा
= 2πrh
= 2 × 2 × 3 × 21 वर्ग मीटर
= 2 × 22 × 3 × 3 वर्ग मीटर
= 396 वर्ग मीटर
95 रु. प्रति वर्ग मीटर की दर से 396 m² पर व्यय
= 396 × 95
= 37620 रु.

परश्न 6.
एक ठोस बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल 616 सेमी. है। इसका वक्र पृष्ठ, सम्पूर्ण पृष्ठ का आधा है, तो बेलन का आयतन ज्ञात कीजिए।
हल:
ठोस बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल
= 2πrh + 2πr²
= 616 सेमी.²
बेलन के वक्र पृष्ठ का क्षेत्रफल
= 2πrh = \(\frac{616}{2}\) सेमी.²
= 308 सेमी.²
बेलन के दोनों वृत्त भागों का क्षेत्रफल
= 2πr²
= 308 सेमी.²
बेलन की त्रिज्या (r) = \(\sqrt{\frac{308}{2 \pi}}\) = \(\sqrt{308 \times \frac{7}{22} \times \frac{1}{2}}\)
= √49 = 7 सेमी.
अत: बेलन की त्रिज्या 7 सेमी. है।

प्रश्न 7.
लोहे का नल 3.5 मीटर लम्बा है तथा उसका बाहरी व्यास 2.6 सेंमी. है। इसकी मोटाई 0.2 सेमी. है। यदि एक घन सेमी. लोहे का वजन 7.8 ग्राम है, तो नल का वजन ज्ञात कीजिए।
हल:
लोहे का नल अर्थात् बेलन की लम्बाई
(h) = 3.5 मी.
= 350 सेमी.
नल का बाहरी व्यास = 2.6 सेमी.
नल की बाहरी त्रिज्या (r₁) = \(\frac{2.6}{2}\) सेमी.
= 1.3 सेमी.
नल की मोटाई = 0.2 सेमी.
नल का आन्तरिक व्यास होगा = 2.6 - 2 (0.2) सेमी.
= 2.6 - 0.4 सेमी.
= 2.2 सेमी.
नल की आन्तरिक त्रिज्या (r₂) होगी = \(\frac{2.2}{2}\) सेमी.
= 1.1 सेमी.
नल के लोहे का आयतन होगा = नल का बाह्य आयतन - नल का आन्तरिक आयतन
= πr₁²h - πr₂²h घन इकाई
= πh(r₁² - r₂²)
= \(\frac{22}{7}\) × 350 {(1.3)2 – (1.1)} घन सेमी.³
= \(\frac{22}{7}\) × 350 (1.69 - 1.21) सेमी.³
= \(\frac{22}{7}\) × 350 × 0.48 सेमी.³
= \(\frac{22}{7}\) × 350 × \(\frac{48}{100}\) सेमी.³
= 22 × 24 सेमी.³ = 528 सेमी.³
∵ एक घन सेमी. लोहे का वजन है = 7.8 ग्राम
∴ 528 घन सेमी. लोहे का वजन होगा
= 7.8 × 528 ग्राम
= 4118.4 ग्राम
= 4.1184 किग्रा.

प्रश्न 8.
एक बन्द शंक्वाकार ठोस के आधार का | क्षेत्रफल 154 वर्ग सेमी. है। यदि ठोस की ऊँचाई 24 सेमी. हो तो ज्ञात कीजिए।
(i) आधार की त्रिज्या
(ii) ढालू लम्बाई
(iii) ठोस का सम्पूर्ण पृष्ठीय क्षेत्रफल।
हल:
(i) यहाँ क्षेत्रफल (आधार का) = 154 व.मी. तथा ऊँचाई (h) = 24 सेमी. है अतः

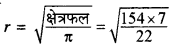
= \(\sqrt{7 \times 7}\)
अतः r = 7 सेमी.

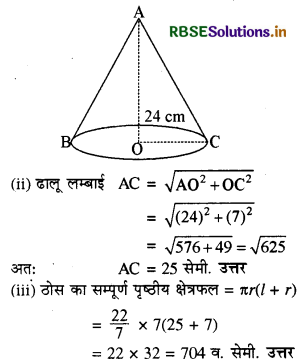
प्रश्न 9.
एक लम्बवृत्तीय शंकु का आयतन 1232 सेमी. है तथा उसकी ऊँचाई 24 सेमी. है। शंकु की तिरछी ऊँचाई ज्ञात कीजिए।
हल:
शंकु का आयतन = 1232 सेमी.³
शंकु की ऊँचाई h = 24 सेमी
∵ शंकु का आयतन = \(\frac{1}{3}\)πr²h

प्रश्न 10.
एक लम्बवृत्तीय शंकु की ऊँचाई और त्रिज्या का अनुपात 12 : 5 है। यदि शंकु का आयतन 8478 सेमी. है, तो शंकु की तिरछी ऊँचाई ज्ञात कीजिए। (π = 3.14 लीजिए)
हल:
लम्बवृत्तीय शंकु की ऊँचाई और त्रिज्या का अनुपात = \(\frac{12}{5}\)
शंकु का आयतन = \(\frac{1}{3}\)πr²h
= 8478 सेमी.³ ....... (i)
∵ \(\frac{h}{r}=\frac{12}{5}\)
∴ h = \(\frac{12}{5}\)r ........ (ii)
समीकरण (ii) से h का मान समी. (i) में रखने पर

प्रश्न 11.
एक सर्कस का टैन्ट 3 मीटर ऊँचाई तक बेलनाकार है। उसके बाद का ऊपरी हिस्सा शंकुनुमा है। यदि आधार का व्यास 105 मीटर और शंकुनुमा भाग की तिर्यक ऊँचाई 53 मीटर हो, तो ज्ञात कीजिए टैन्ट को बनाने में कितने वर्ग मीटर कपड़ा काम में आया?
हल:
कुल कपड़ा काम में आया = बेलनाकार भाग का वक्र पृष्ठ का क्षेत्रफल + शंकु के वक्र पृष्ठ का क्षेत्रफल
= 2πrh + πrl
[यहाँ r = \(\frac{105}{2}\) = 52.5 मी. है]
और 1 = 3 मी., 1 = 53 मी. . कुल कपड़ा काम में आया
= [2 × \(\frac{22}{7}\) × 52.5 × 3 + \(\frac{22}{7}\) × 52.5 × 55] मी.²
= \(\frac{22}{7}\) × 52.5 (6 + 53) मी.²
= \(\frac{22}{7}\) × 52.5 × 59

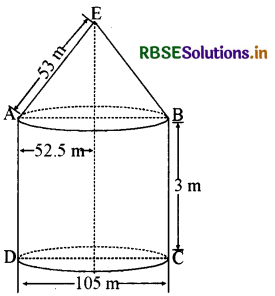
= 22 × 7.5 × 59 = 165 × 59
= 9735 मी.²

प्रश्न 12.
मोनिका के पास केनवास का एक टुकड़ा है जिसका क्षेत्रफल 551 m² है। वह इससे 7 m आधार त्रिज्या वाले एक शंकु के आयतन का तम्बू बनवाती है। यह मानते हुए कि सिलाई और कटाई में लगभग 1 m केनवास नष्ट हुआ होगा, इससे बनाए जाने वाले शंकु का आयतन ज्ञात कीजिए।
हल:
केनवास का क्षेत्रफल = 551 m² है और 1 m² केनवास सिलाई इत्यादि में नष्ट हो जाता है।
अतः तम्बू के लिए उपलब्ध केनवास
= (551 - 1) m² = 550 m²
इसलिए, तम्बू का पृष्ठीय क्षेत्रफल = 550 m²
अब, तम्बू के आधार की त्रिज्या = 7 m
ध्यान दीजिए कि तम्बू की केवल वक्र पृष्ठ ही होती है (तम्बू के फर्श को ढका नहीं जाता है)।
अतः तम्बू का वक्र पृष्ठीय क्षेत्रफल = 550 m²
अर्थात् πrl = 550
या \(\frac{22}{7}\) × 7 × 1 = 550
या l = \(\frac{550}{22}\) m = 25 m
इसलिए h = \(\sqrt{l^{2}-r^{2}}\) = \(\sqrt{25^{2}-7^{2}}\) m
अब, l² = r² + h²
= \(\sqrt{625-49}\) m
= √576 m
= 24 m
अतः तम्बू का आयतन
= \(\frac{1}{3}\)πr²h = \(\frac{1}{3} \times \frac{22}{7}\) × 7 × 7 × 24 m³
= 1232 m³ उत्तर

प्रश्न 13.
एक बेलन सीसे का बना हुआ है, जिसकी त्रिज्या 4 सेमी. और ऊँचाई 10 सेमी. है। इसे पिघलाकर 2 सेमी. त्रिज्या के कितने गोले बनाए जा सकते हैं?
हल:
बेलन की त्रिज्या = 4 सेमी.
बेलन की ऊँचाई = 10 सेमी.
बेलन का आयतन = πr²h घन इकाई

प्रश्न 14.
12 सेमी. व्यास का एक बेलनाकार पात्र जल से अंशतः भरा हुआ है। यदि उसमें 6 सेमी. व्यास का एक गोला पूर्णतः डुबो दिया जाता है। ज्ञात कीजिए कि बेलनाकार पात्र में जल की सतह कितनी ऊँचाई तक उठ जाएगी?
हल:
गोले का व्यास = 6 सेमी.
गोले की त्रिज्या (r) = 3 सेमी.
गोले का आयतन होगा = \(\frac{4}{3}\)πr³
= \(\frac{4}{3}\) × \(\frac{22}{7}\) × 3 × 3 × 3 घन सेमी.
= \(\frac{22}{7}\) × 36 सेमी.³
= \(\frac{792}{7}\) सेमी.³
बेलन का व्यास = 12 सेमी.
बेलन की त्रिज्या = \(\frac{12}{2}\) = 6 सेमी.
∵ गोले को पानी में डालने पर बेलन के पानी वाले भाग का आयतन बढ़ेगा
= \(\frac{792}{7}\) सेमी.³
∴ पानी की सतह की ऊँचाई होगी
= \(\frac{792}{7}\) ÷ πr²

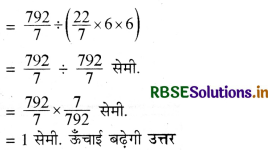
प्रश्न 15.
किसी भवन का ऊपरी भाग | अर्धगोलाकार है और इस पर पेंट किया जाना है (देखिए आकृति )। यदि इस अर्धगोले के आधार की परिधि 17.6 m है, तो 5 रुपये प्रति 100 cm- की दर से इसे पेंट कराने का व्यय ज्ञात कीजिए।

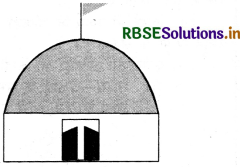
हल:
चूँकि केवल गोलाकार पृष्ठ पर ही पेंट होगा, इसलिए हमें अर्धगोले के वक्र पृष्ठीय क्षेत्रफल को ज्ञात करने की आवश्यकता है।
अब, आधार की परिधि = 17.6 m है।
इसलिए 2πr = 17.6
अर्थात् = \(\frac{17.6 \times 7}{2 \times 22}\)m = 2.8 m
इसलिए, भवन का वक्र पृष्ठीय क्षेत्रफल = 2πr²
= 2 × \(\frac{22}{7}\) × 2.8 × 2.8 m²
= 49.28 m²
अब 100 cm² पेंटिंग की लागत = 5 रुपये
इसलिए, 1 m² पेंटिंग की लागत = 500 रुपये
अतः 49.28 m² पेंटिंग की लागत
= 500 × 49.28 रुपये
= 24640 रुपये