RBSE Class 9 Maths Important Questions Chapter 12 Heron’s Formula

Rajasthan Board RBSE Class 9 Maths Important Questions Chapter 12 Heron’s Formula Important Questions and Answers.

RBSE Class 9 Maths Chapter 12 Important Questions Heron’s Formula

I. Multiple Choice Questions :
Choose the correct answer from the given four options.

Question 1.
If the area of equilateral triangle is 16√3 cm², then the perimeter of the triangle is :
(a) 48 cm
(b) 24 cm
(c) 12 cm
(d) 36 cm
Answer:
(b) 24 cm

Question 2.
The edge of a triangular board are 6 cm, 8 cm and 10 cm. The cost of painting it at the rate of 9 paise per cm² is :
(a) ₹ 2.00
(b) ₹ 2.16
(c) ₹ 2.48
(d) ₹ 3.00
Answer:
(b) ₹ 2.16

Question 3.
If the perimeter of a rhombus is 80 cm and one of its diagonals is 24 cm, then the length of the other diagonal is:
(a) 16 cm
(b) 20 cm
(c) 32 cm
(d) 48 cm
Answer:
(c) 32 cm

Question 4.
If the perimeter of an equilateral triangle is 60 m, then the area is :
(a) 10√3 m²
(b) 15√3 m²
(c) 20√3 m²
(d) 100√3m²
Answer:
(d) 100√3m²

Question 5.
An isosceles right triangle has area 8 cm2. The length of its hypotenuse is :
(a) √32 cm
(b) √l6 cm
(c) √48 cm
(d) √24 cm
Answer:
(a) √32 cm

Question 6.
If the sides of a triangle are 56 cm, 65 cm and 52 cm long, then the area of the triangle is :
(a) 1322 cm²
(b) 1311 cm²
(c) 1344 cm²
(d) 1392 cm²
Answer:
(c) 1344 cm²

Question 7.
If the side of a parallelogram are 9 cm and 4 cm, then the ratio of their corresponding altitudes is :
(a) 2 : 3
(b) 3 : 2
(c) 9 : 4
(d) 4 : 9
Answer:
(d) 4 : 9

Question 8.
The sides of a triangle are 35 cm, 54 cm and 61 cm. The length of its longest altitude is:
(a) 16√5 cm
(b) 10√5 cm
(c) 24√5 cm
(d) 28 cm
Answer:
(c) 24√5 cm

Question 9.
The sides of a triangle are in the ratio of 5 : 12 : 13 and its perimeter is 150 cm. The area of the triangle is :
(a) 375 cm²
(b) 750 cm²
(c) 250 cm²
(d) 500 cm²
Answer:
(b) 750 cm²

Question 10.
Each of the equal sides of an isosceles triangle is 13 cm and its base is 24 cm. The area of the triangle is:
(a) 156 cm²
(b) 78 cm²
(c) 60 cm²
(d) 120 cm²
Answer:
(c) 60 cm²

Question 11.
The base of right triangle is 48 cm and its hypotenuse is 50 cm long. The area of the triangle is :
(a) 168 cm²
(b) 252 cm²
(c) 336 cm²
(d) 504 cm²
Answer:
(c) 336 cm²

Question 12.
The base of an isosceles triangle is 8 cm long and each of its equal sides measures 6 cm. The area of the triangle is :
(a) 16√5 cm²
(b) 8√5 cm²
(c) 16√3 cm²
(d) 8√3 cm²
Answer:
(b) 8√5 cm²

Question 13.
Each side of an equilateral triangle is 10 cm long. The height of the triangle is :
(a) 10√3 cm
(b) 5√3 cm
(c) 10√2 cm
(d) 5 cm
Answer:
(b) 5√3 cm

Question 14.
The area of an equilateral triangle is 81 /3 cm2, its height is :
(a) 9√3 cm
(b) 6√3 cm
(c) 18√3 cm
(d) 9 cm
Answer:
(a) 9√3 cm

Question 15.
The lengths of the three sides of a triangular field are 40 m, 24 m and 32 m respectively. The area of the triangle is :
(a) 480 m²
(b) 320 m²
(c) 384 m²
(d) 360 m²
Answer:
(c) 384 m²

II. Fill in the Blanks:

Question 1.
Area of trapezium with parallel sides 'a' and 'b' and the distance between two parallel sides as h = ___________ .
Answer:
\(\frac{1}{2}\)(a + b) × h

Question 2.
Heron's foumula is stated as :
Area of a triangle ABC = ____________
Where s = ____________
a, b, c, = ____________
Answer:
\(\sqrt{s(s-a)(s-b)(s-c)}\), semiperimeter, sides of the triangle,

Question 3.
The semiperimeter of a triangle having the length of its sides as 20 cm, 15 cm and 9 cm is ____________ .
Answer:
22 cm

Question 4.
The perimeter of an equilateral triangle is 60 m. The area is ____________ .
Answer:
100√3 cm²

Question 5.
The sides of a triangle are 56 cm, 60 cm and 52 cm long, then the area of the triangle is ____________.
Answer:
1344 cm²

III. True/False:
State whether the following statements are True or False.

Question 1.
Heron formula for area of triangle is not valid of all triangles.
Answer:
False

Question 2.
If each side of the triangles is tripled, the area will becomes 9 times.
Answer:
True

Question 3.
Base and corresponding altitude of the parallelogram are 8 and 5 cm respectively. Area of parallelogram is 40 cm².
Answer:
True

Question 4.
If each side of triangle is doubled, the perimeter will become 4 times.
Answer:
False

Question 5.
If p is the perimeter of the triangle of sides a, b, c, the area of triangle is
A = \(\frac{1}{4}\sqrt{p(p-2 a)(p-2 b)(p-2 c)}\).
Answer:
True

Question 6.
When two triangles are congruent, there areas are same.
Answer:
True

Question 7.
Heron belongs to America.
Answer:
False

Question 8.
If the side of the equilateral triangle is a rational number, the area would always be irrational number.
Answer:
True

IV. Match the Columns:

Match the column I with the column II.

Column I	Column II
(1) Perimeter of rectangle of length 24 cm and diagonal 26 cm	(i) 22 cm
(2) Perimeter of the square of side 10 cm	(ii) 17 cm
(3) Perimeter of triangle of sides 4, 5, 8 cm	(iii) 40 cm
(4) Perimeter of parallelogram of two sides 5 and 6 cm respectively	(iv) 68 cm

Answer:

Column I	Column II
(1) Perimeter of rectangle of length 24 cm and diagonal 26 cm	(iv) 68 cm
(2) Perimeter of the square of side 10 cm	(iii) 40 cm
(3) Perimeter of triangle of sides 4, 5, 8 cm	(ii) 17 cm
(4) Perimeter of parallelogram of two sides 5 and 6 cm respectively	((i) 22 cm

V. Very Short Answer Type Questions:

Question 1.
Find the area of ∆ABC in which AB = BC = 4 cm and ∠B = 90°.
Answer:

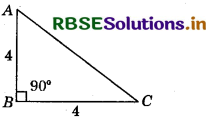
From the figure, ∆ABC is a right-angled triangle.
∴ Area of AABC = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × (BC) × (AB) = \(\frac{1}{2}\) × 4 × 4 = 8 cm²
∴ ar(∆ABC) = 8 cm².

Question 2.
Find the side of an isosceles right triangle of hypotenuse 5√2 cm.
Answer:

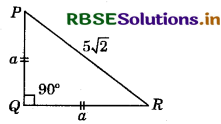
According to the question :
PQ - QR = a (say)
PR = 5√2
∴ By Pythagoras theorem: P² + B² = H²
a² + a² = (5√2)²
⇒ 2a² = 50
⇒ a² = \(\frac{50}{2}\)
⇒ a² = 25
⇒ a = 5 cm
Hence, equal sides of isosceles triangle are 5 cm each. 

Question 3.
The perimeter of an equilateral triangle is 60 m. Find its area.
Answer:
Let side of equilateral be 'a'.
Now, perimeter = 3a
⇒ 3a = 60 m
⇒ a = \(\frac{60}{3}\) = 20 m
Then, area of equilateral triangle = \(\frac{\sqrt{3}}{4}\)(side)²
⇒ area of equilateral triangle = \(\frac{\sqrt{3}}{4}\) × (20)² = \(\frac{\sqrt{3}}{4}\)  × 20 × 20 = 100√3
∴ Area = 100 √3 m².

Question 4.
Area of an isosceles right triangle is 8 cm². Find its hypotenuse.
Answer:

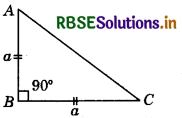
Let ABC be an isosceles right triangle, where
∠B = 90°
Let AB = BC = a
Now, area of ∆ABC = \(\frac{1}{2}\) × base × height
⇒ 8 = \(\frac{1}{2}\) × a × a
⇒ a² = 16
⇒ a = 4
Now, by Pythagoras theorem
AB² + BC² = AC²
⇒ a² = a² = AC²
⇒ (4) + (4) = AC²
⇒ 16 + 16 = AC²
⇒ AC² = 32
⇒ AC = √32
⇒ AC = 4√2 cm
∴ Hypotenuse = 4√2 cm.

VI. Short Answer Type Questions:

Question 1.
If the length of median of an equilateral triangle be x cm, then find its area.
Answer:
Let ABC be an equilateral triangle of side ‘a’ cm. A
Also, we know that in an equilateral triangle, the median and perpendicular coincide with each other.

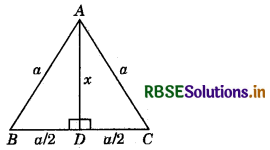
∴ AD ⊥ BC and D is mid-point of BC.

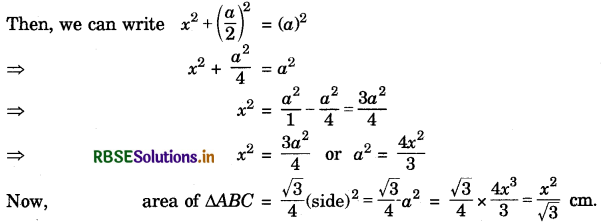
Question 2.
The sides of a triangle are 7 cm, 24 cm and 25 cm. What is its area?
Answer:
Since, sides are given, we use Heron’s formula to find area of triangle.
Let a = 7 cm, b = 24 cm and d = 25 cm
s = \(\frac{a+b+c}{2}\) = \(\frac{7+24+25}{2}=\frac{56}{2}\) = 28
∴ Area = \(\sqrt{s(s-a)(s-b)(s-c)}\)
∴ Area =  A = \(\sqrt{28(28-7)(28-24)(28-25)}\)
⇒ A = \(\sqrt{28 \times 21 \times 4 \times 3}\)
⇒ A = \(\sqrt{2 \times 2 \times 7 \times 7 \times 3 \times 2 \times 2 \times 3}\)
⇒ A = 2 × 7 × 3 × 2 = 84
Hence, area of triangle = 84 cm²

Question 3.
The edges of a triangular board are 6 cm, 8 cm and 10 cm. Find the cost of painting it at the rate of 9 paise per cm².
Answer:

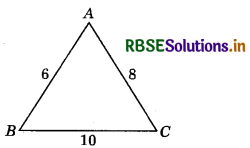
Let a = 10 cm, b = 8 cm and c = 6 cm
Then, s = \(\frac{a+b+c}{2}\) = \(\frac{10+8+6}{2}\) = \(\frac{24}{2}\) = 12
∴ Area = \(\sqrt{12(12-10)(12-8)(12-6)}\)
⇒ Area = \(\sqrt{12 \times 2 \times 4 \times 6}\) = 24
∴ Area = 24 cm²
Now, cost of painting the board at the rate of 9 paise per cm²
= 24 × 0.09 = ₹ 2.16 (∵ 9 paise = ₹ 0.09)
Hence, cost of painting = ₹ 2.16.

Question 4.
In figure, P and Q are two lamp posts. If the area of the ∆PDC is same as that of the rectangle ABCD, find the distance between the two lamp posts.

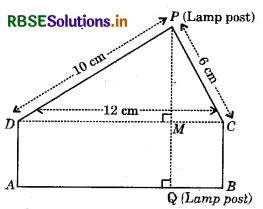
Answer:
In ∆PCD,
a = 12 cm, 6 = 6 cm, c = 10 cm.
s = \(\frac{12+6+10}{2}\) cm = 14 cm.

Question 5. 
A municipal corporation wall on road side has dimensions as shown in figure. The wall is to be used for advertisements and it yields an earning of  ₹ 400 per m² in a year. Find the total amount of revenue earned in a year.
Answer: 

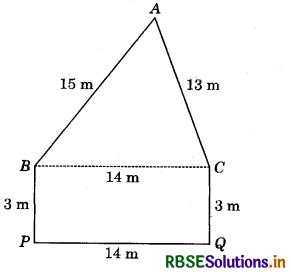
We can find the total area of the wall in two parts. One parts triangular, i.e. ∆ABC at the top and the second part is rectangular, i.e. rectangle PQCB at the bottom.
In triangular part, a = 14 m, b = 13 m, c = 15 m.

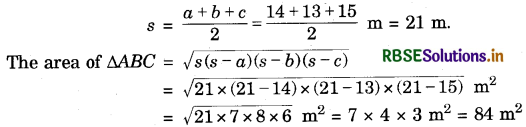
The area of rectangle PQCB = 14 × 3 m² = 42 m².
Total area of the wall = 84 m² + 42 m² = 126 m²
Total amount of revenue earned in a year at the rate of  ₹ 400/m²
= ₹ 400 × 126 = ₹ 50,400

Question 6.
Find the area of the pentagon ABCDE shown in figure.
Answer:
In triangle BCD, ∠C = 90°, therefore, by Pythagoras theorem,
BD = \(\sqrt{B C^{2}+C D^{2}}\) = \(\sqrt{4^{2}+3^{2}}\) cm
= \(\sqrt{16+9}\) cm = √25 cm = 5 cm
Again in ∆ABD, ∠ABD = 90°, therefore, by Pythagoras theorem,

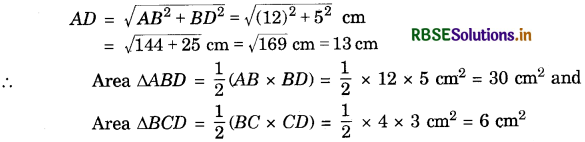
Next, we find area ∆ADE using Heron’s formula

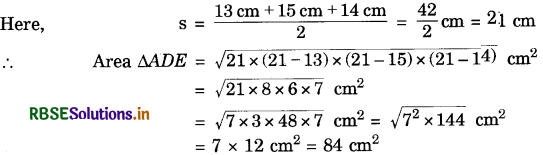
Hence, the area of the pentagon ABCDE
= area ∆ABD + area ∆BCD + area ∆ADE
= (30 + 6 + 84) cm² = 120 cm²

Question 7.
The sides of a triangular park are 8 m, 10 m and 6 m respectively. A small circular area of diameter 2 m is to be left out and the remaining area is to.be used for growing roses. How much area is used for growing roses? (take π = 3.14)
Answer:
Let sides of a triangle be a = 8 m, b = 10 m and c = 6 m
Now, semi-perimeter of a triangle, s = \(\frac{a+b+c}{2}\)
= \(\frac{8+10+6}{2}\) = \(\frac{24}{2}\)= 12 m
Area of a triangle = \(\sqrt{s(s-a)(s-b)(s-c)}\) 
= \(\sqrt{12(12-8)(12-10)(12-6)}\)
= \(\sqrt{12 \times 4 \times 2 \times 6}\) = 24 m²
and area of a circle = πr² = 3.14 × 1²
= 3.14 m² 
∴ Ares for growing roses = Area of a triangle - area of a circle
= 24 - 3.14 = 20.86 m²

VII. Long Answer Type Questions:

Question 1.
The length of the sides of a triangle are in the ratio 3:4:5 and its perimeter is 144 cm. Find :
(i) the area of the triangle, and
(ii) the height corresponding to the longest side.
Answer:
Given, perimeter = 144 cm
Ratio of sides = 3:4:5
Let the sides be 3x, 4x and 5x
∴ 3x + 4x + 5x = 144
12x = 144
x = 12
1st side, 3x = 3 × 12 = 36 cm
Ilnd side, 4x = 4 × 12 = 48 cm
Illrd side, 5x = 5 × 12 = 60 cm
∴ a = 3x, b = 4x, c = 5x
Now, semi-perimeter of the triangle,
s = \(\frac{a+b+c}{2}\) = \(\frac{36+48+60}{2}\) = \(\frac{144}{2}\) = 72cm

(i) Area of triangle = \(\sqrt{s(s-a)(s-b)(s-c)}\) (By Heron’s formula)
= \(\sqrt{72 \times(72-36)(72-48)(72-60)}\)
= \(\sqrt{72 \times 36 \times 24 \times 12}\)
= \(\sqrt{(36)^{2} \times(24)^{2}}\)
= 36 × 24 = 864 cm² .
Hence, the area of the given triangle is 864 cm².

(ii) Let height of a triangle be h cm.
Then, area of triangle = \(\frac{1}{2}\) × base × height
⇒ 864 = \(\frac{1}{2}\) × 60 × h
(Since, longest side of a triangle is 60 cm, so we consider it as base of the triangle.)
⇒ 864 = 30h ⇒ h = 28.8 cm
Hence, the height corresponding to the longest side is 28.8 cm.

Question 2.
A rectangular plot is given for constructing a house having a measurement of 40 m long and 15 m in the front.
According to the laws, a minimum of 3 m wide space should be left in the front and back each and 2 m wide space on each of other sides. Find the largest area, where house can be constructed.
Answer:

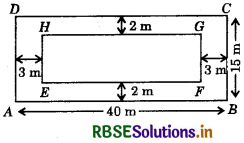
Let ABCD be a rectangular plot having a measurement of 40 m long and 15 m front. 
⇒ Length of inner rectangle 
= EF = 40 - 3 - 3 = 34 m 
and breadth of inner rectangle 
= FG = 15 - 2 - 2 = 11 m
Now, when space are left according to the law, then
∴ Area of inner rectangle, EFGH
= EF × FG = 34 × 11 = 374 m² (∵ Area of a rectangle = length × breadth)
Hence, the largest area, where the house can be constructed, is 374 m².

Question 3.
A design is made on a rectangular tile of dimensions 50 cm x 70 cm as shown in figure. Find the total area of the design and the remaining area of the tile.

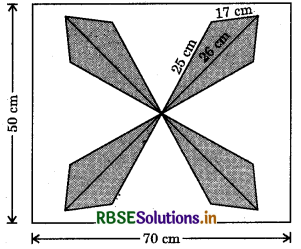
Answer:
We have 
Area of the rectangular tile
= (length × breadth) sq. units
= (50 × 70) cm² = 3500 cm²
For area of each triangle
Let a = 26 cm, b = 17 cm, c = 25 cm
s = \(\frac{a+b+c}{2}\) units
s = \(\frac{26+17+25}{2}\) = \(\frac{68}{2}\) = 34 cm
s - a = 34 - 26 = 8cm
s - b = 34 - 17 = 17 cm
s - c = 34- 25 = 9 cm
Area of each triangle = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{34 \times 8 \times 17 \times 9}\)9 = \(\sqrt{2 \times 17 \times 2 \times 2 \times 2 \times 17 \times 9}\)
= 12 × 17 = 204 cm²
∴ Total area of design = 8 × area of one triangle
= (8 × 204) cm² = 1632 cm²
So,remaining area of the tile = Area of rectangular tile - total area of the design
= 3500 - 1632 = 1868 cm²