RBSE Class 9 Maths Important Questions Chapter 12 हीरोन सूत्र

Rajasthan Board RBSE Class 9 Maths Important Questions Chapter 12 हीरोन सूत्र Important Questions and Answers.

RBSE Class 9 Maths Chapter 12 Important Questions हीरोन सूत्र

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
एक समबाहु त्रिभुज की भुजा 6 सेमी है, तो त्रिभुज का क्षेत्रफल होगा
(A) 6√3 वर्ग सेमी.
(B) 9√3 वर्ग सेमी.
(C) 16√3 वर्ग सेमी.
(D) 3√3 वर्ग सेमी.
उत्तर:
(B) 9√3 वर्ग सेमी.

प्रश्न 2.
यदि किसी त्रिभुज की भुजाएँ क्रमशः 50 cm, 78 cm तथा 112 cm हों, न्यूनतम लम्ब की लम्बाई होगी
(A) 40 cm
(B) 50 cm
(C) 20 cm
(D) 30 cm
उत्तर:
(D) 30 cm

प्रश्न 3.
एक त्रिभुज की भुजाएँ 40 cm, 70 cm तथा 90 cm हैं, त्रिभुज का क्षेत्रफल होगा
(A) 600√5 cm²
(B) 500√6 cm²
(C) 482√5 cm²
(D) 60√5 cm²
उत्तर:
(A) 600√5 cm²

प्रश्न 4.
यदि s = 66 cm, a = 60 cm, b = 61 cm तथा c= 11 cm हों, तो त्रिभुज का क्षेत्रफल है
(A) 240 cm
(B) 330 cm
(C) 310 cm
(D) 316 cm
उत्तर:
(B) 330 cm

प्रश्न 5.
हीरोन का सूत्र है
(A) \(\sqrt{(s-a)(s-b)(s-c)}\)
(B) \(\sqrt{(s-a) \div(s-b) \times(s-c)}\)
(C) \(\sqrt{s(s-a)(s-b)(s-c)}\)
(D) \(\frac{s}{\sqrt{(s-a)(s-b)(s-c)}}\)
उत्तर:
(C) \(\sqrt{s(s-a)(s-b)(s-c)}\)

प्रश्न 6.
समबाहु त्रिभुज की एक भुजा a है तो इसका परिमाप है
(A) 3a
(B) 2a
(C) 4a
(D) 5a
उत्तर:
(A) 3a

प्रश्न 7.
समद्विबाहु त्रिभुज का अर्द्ध-परिमाप है
(A) (2a × b)
(B) (2a + b)
(C) \(\left(\frac{2 a \times b}{3}\right)\)
(D) \(\left(\frac{2 a+b}{2}\right)\)
उत्तर:
(D) \(\left(\frac{2 a+b}{2}\right)\)

प्रश्न 8.
एक समद्विबाहु त्रिभुज का क्षेत्रफल होगा, यदि इसकी समान भुजा 6 cm एवं अन्य भुजा 8 cm हो
(A) 8√5 cm²
(B) 5√8 cm²
(C) 3√55 cm²
(D) 3√8 cm²
उत्तर:
(A) 8√5 cm²

प्रश्न 9.
4√3 cm² क्षेत्रफल वाले समबाहु त्रिभुज की प्रत्येक भुजा की लम्बाई होगी- ।
(A) 4 cm
(B) \(\frac{4}{\sqrt{3}}\) cm
(C) \(\frac{\sqrt{3}}{4}\) cm
(D) 3 cm
उत्तर:
(A) 4 cm

प्रश्न 10.
एक समबाहु त्रिभुज का परिमाप 12 cm है, इसका क्षेत्रफल होगा
(A) 12√5
(B) 24√3
(C) 36√3
(D) 4√3
उत्तर:
(D) 4√3

प्रश्न 11.
यदि किसी त्रिभुज की प्रत्येक भुजा को दो गुना कर दिया जाए, तो त्रिभुज के क्षेत्रफल में वृद्धि होगी
(A) 100√2%
(B) 200%
(C) 300%
(D) 400%
उत्तर:
(C) 300%

प्रश्न 12.
यदि किसी समबाहु त्रिभुज की माध्यिका की लम्बाई x सेमी. है, तब इसका क्षेत्रफल होगा
(A) x²
(B) \(\frac{\sqrt{3}}{2}\)x²
(C) \(\frac{x^{2}}{2}\)
(D) \(\frac{x^{2}}{\sqrt{3}}\)
उत्तर:
(D) \(\frac{x^{2}}{\sqrt{3}}\)

प्रश्न 13.
किसी त्रिभुज की भुजाएँ 16 सेमी., 30 सेमी. व 34 सेमी. हैं। तब इसका क्षेत्रफल है
(A) 225 सेमी.²
(B) 225√3 सेमी²
(C) 225√2 सेमी.²
(D) 450 सेमी.2²
उत्तर:
(B) 225√3 सेमी²

प्रश्न 14.
किसी समद्विबाहु समकोण त्रिभुज का आधार 30 सेमी. है। इस त्रिभुज का क्षेत्रफल है
(A) 225 सेमी.
(B) 225√2 सेमी.
(C) 450 सेमी.
(D) 225√3 सेमी.
उत्तर:
(A) 225 सेमी.

प्रश्न 15.
यदि किसी समद्विबाहु समकोण त्रिभुज का क्षेत्रफल 8 सेमी. है, तब त्रिभुज का परिमाप है
(A) 8 + √2 सेमी.
(B) 8 + 4√2 सेमी.
(C) 4 + 8√2 सेमी.
(D) 12√2 सेमी.
उत्तर:
(B) 8 + 4√2 सेमी.

प्रश्न 16.
यदि किसी समबाहु त्रिभुज की प्रत्येक भुजा को तीन गुना कर दिया जाये तब त्रिभुज के क्षेत्रफल में प्रतिशत वृद्धि होगी
(A) 400%
(B) 900%
(C) 300%
(D) 800%
उत्तर:
(D) 800%

प्रश्न 17.
यदि एक वर्ग एवं एक समबाहु त्रिभुज का परिमाप समान है। यदि वर्ग के विकर्ण की लम्बाई 12√2 सेमी. है, तब वर्ग का क्षेत्रफल है
(A) 64√3 सेमी.²
(B) 24√2 सेमी.²
(C) 24√3 सेमी.²
(D) 48√3 सेमी.²
उत्तर:
(A) 64√3 सेमी.²

प्रश्न 18.
किसी त्रिभुज के परिमाप की लम्बाई 144 मीटर है और उसकी भुजाओं का अनुपात 3 : 4 : 5 है। त्रिभुज का क्षेत्रफल है
(A) 636 मी.²
(B) 646 मी.²
(C) 546 मी.²
(D) 464 मी.²
उत्तर:
(B) 646 मी.²

प्रश्न 19.
किसी समबाहु त्रिभुज की ऊँचाई 1 सेमी. है। तब इसका क्षेत्रफल है
(A) \(\frac{h^{2}}{\sqrt{3}}\)
(B) \(\frac{h}{\sqrt{3}}\)
(C) √3h
(D) 3√h
उत्तर:
(A) \(\frac{h^{2}}{\sqrt{3}}\)

प्रश्न 20.
यदि किसी त्रिभुज का क्षेत्रफल A है। त्रिभुज की भुजाओं की लम्बाई दोगुनी करने पर त्रिभुज का क्षेत्रफल होगा
(A) 3A
(B) 16A
(C) 2A
(D) 4A
उत्तर:
(D) 4A

रिक्त स्थानों की पूर्ति करो

प्रश्न 1.
किसी त्रिभुज की भुजाएँ a, b व c हैं, तब उसका . अर्द्धपरिमाप s = ________ एवं क्षेत्रफल = _________
उत्तर:
\(\frac{a+b+c}{2}, \sqrt{s(s-a)(s-b)(s-c)}\)

प्रश्न 2.
यदि किसी समद्विबाहु त्रिभुज की दो समान भुजाओं की लम्बाई a एवं तीसरी भुजा की लम्बाई b है, तब समद्विबाहु त्रिभुज का क्षेत्रफल ________
उत्तर:
\(\frac{b}{a} \sqrt{4 a^{2}-b^{2}}\)

प्रश्न 3.
समबाहु त्रिभुज जिसकी प्रत्येक भुजा की लम्बाई a है, तब क्षेत्रफल = ________
उत्तर:
\(\frac{\sqrt{3}}{4}\)a²

प्रश्न 4.
एक समषटभुज, जिसकी प्रत्येक भुजा a लम्बाई की है, का क्षेत्रफल = ________
उत्तर:
\(\frac{3 \sqrt{3}}{4}\)a²

प्रश्न 5.
यदि किसी त्रिभुज की भुजाओं की लम्बाई को दोगुना कर दिया जाये, तब उसका क्षेत्रफल _________ गुना हो जाता है।
उत्तर:
चार

प्रश्न 6.
किसी समबाहु त्रिभुज की ऊँचाई 5√3 सेमी. है। तब इस त्रिभुज का क्षेत्रफल ________ है।
उत्तर:
25√3 सेमी.²

प्रश्न 7.
यदि किसी समचतुर्भुज की भुजा की लम्बाई 10 सेमी. एवं विकर्ण की लम्बाई 16 सेमी. है तब समचतुर्भुज का क्षेत्रफल ________ है।
उत्तर:
96 सेमी.²

प्रश्न 8.
एक समबाहु त्रिभुज का परिमाप 60 मीटर है। तब इस त्रिभुज का क्षेत्रफल ________ है।
उत्तर:
100√3 सेमी.²

सत्य/असत्य-निम्नलिखित कथनों के लिए सत्य अथवा असत्य लिखिए

प्रश्न 1.
किसी समद्विबाहु समकोण त्रिभुज का क्षेत्रफल उसकी दोनों भुजाओं, जो समकोण बनाती हैं, के गुणनफल के बराबर होता है।
उत्तर:
असत्य

प्रश्न 2.
किसी समकोण त्रिभुज ABC का क्षेत्रफल 8 सेमी. होगा जबकि AB = AC = 4 सेमी. और ∠A = 90°
उत्तर:
सत्य

प्रश्न 3.
एक त्रिभुज की भुजाओं का अनुपात 12 : 17 : 25 है और उसका परिमाप 540 सेमी. है। इस त्रिभुज का क्षेत्रफल 900 सेमी. है।
उत्तर:
असत्य

प्रश्न 4.
किसी समबाहु त्रिभुज की ऊँचाई । सेमी है तब इसका क्षेत्रफल \(\frac{h^{2}}{\sqrt{3}}\) होगा।
उत्तर:
सत्य

प्रश्न 5.
यदि किसी त्रिभुज की प्रत्येक भुजा को दोगुना कर दिया जाए, तो त्रिभुज का क्षेत्रफल 400 प्रतिशत बढ़ जायेगा।
उत्तर:
असत्य

प्रश्न 6.
यदि क़िसी समबाहु त्रिभुज की प्रत्येक भुजा को तीन गुना कर दिया जाये तब त्रिभुज के क्षेत्रफल में 800% की वृद्धि होगी।
उत्तर:
सत्य

प्रश्न 7.
यदि किसी समद्विबाहु समकोण त्रिभुज का क्षेत्रफल 8 सेमी. है, तब त्रिभुज का परिमाप 4 + 8√2 सेमी. होगा।
उत्तर:
असत्य

प्रश्न 8.
किसी त्रिभुज का परिमाप की लम्बाई 144 मीटर है और उसकी भुजाओं का अनुपात 3 : 4 : 5 है तब त्रिभुज का क्षेत्रफल 646 मीटर होगा।
उत्तर:
सत्य

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
यदि a, b, c त्रिभुज की भुजाएँ हैं तो त्रिभुज का अर्द्ध-परिमाप लिखिए।
हल:
अर्द्ध-परिमाप = \(\frac{a+b+c}{2}\)

प्रश्न 2.
यदि किसी त्रिभुज की भुजाएँ क्रमशः 3 m, 4 m तथा 5 m हों, तो त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
हल:
s = \(\frac{a+b+c}{2}=\frac{3+4+5}{2}=\frac{12}{2}\) = 6 cm
∴ Δ का क्षेत्रफल = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{6(6-3)(6-4)(6-5)}\)
= \(\sqrt{6 \times 3 \times 2 \times 1}\)
= \(\sqrt{36}\) = 6 m²

प्रश्न 3.
एक समबाहु त्रिभुज की भुजा की लम्बाई ज्ञात कीजिये, जिसका क्षेत्रफल 16√3 cm है।
हल:
समबाहु त्रिभुज का क्षेत्रफल = \(\frac{\sqrt{3}}{4}\)a²
⇒ 16√3 = 3 × (भुजा)
16 × 4 = (भुजा)
∴ भुजा = \(\sqrt{64}\)
= 8 cm
अतः समबाहु Δ की भुजा की लम्बाई = 8 cm

प्रश्न 4.
संलग्न चित्र में भुजा PS तथा SR का अनुपात 3 : 2 है। यदि ΔPQR का क्षेत्रफल 40 cm- हो, तो ΔQSR का क्षेत्रफल बताइए।

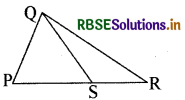
हल:
16 cm²

लघूत्तरात्मक प्रश्न

प्रश्न 1.
एक त्रिभुज का क्षेत्रफल ज्ञात कीजिये जिसकी दो भुजायें 8 cm और 11 cm हैं और जिसका परिमाप 32 cm ( देखिये आकृति) है।

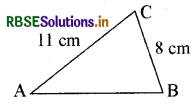
हल:
दिया गया है
त्रिभुज का परिमाप = 32 cm
a = 8 cm, b = 11 cm है।

∴ तीसरी भुजा C = 32 - (8 + 11)
= 32 - 19 = 13 cm

अब 2s = 32 है ∴ s = 16 cm
s - a = (16 - 8) = 8 cm
s - b = (16 - 11) cm = 5 cm
s - C = (16 - 13) cm = 3 cm

∴ त्रिभुज का क्षेत्रफल
= \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{16 \times 8 \times 5 \times 3}\)
= 8\(\sqrt{30}\) cm²

प्रश्न 2.
एक त्रिभुजाकार पार्क ABC की भुजायें 120 m, 80 m और 50 m हैं ( देखिये आकृति)। एक मालिन धनिया को इसके चारों ओर एक बाड़ लगानी है और इसके अन्दर घास उगानी है। उसे कितने क्षेत्रफल में घास उगानी है? एक ओर 3 m चौड़े एक फाटक के लिये स्थान छोड़ते हुए इसके चारों ओर 20 रु. प्रति मीटर की दर से काँटेदार बाड़ लगाने का व्यय भी ज्ञात कीजिये।

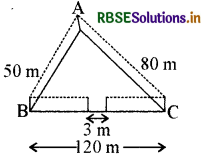
हल:
2s = 50 m + 80 m + 120 m
= 250 m
अर्थात् s = 125 m
∴ s - a = 125 - 120 = 5 m
s - b = 125 - 80 = 45 m
s - c = 125 - 50 = 75 m

अतः घास उगाने के लिए क्षेत्रफल
= \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{125 \times 5 \times 45 \times 75}\)
= 375\(\sqrt{15}\) m²

पार्क का परिमाप = AB + BC + CA = 250 m
अतः बाड़ लगाने के लिए आवश्यक तार की लम्बाई
= 250 m - 3 m (फाटक के लिये)
= 247 m

∴ बाड़ लगाने का व्यय = 20 × 247
= 4940 रु.

प्रश्न 3.
निम्नलिखित के क्षेत्रफल ज्ञात कीजिए
(i) समबाहुं त्रिभुज जिसका परिमाप 60 सेमी. है।
(ii) समद्विबाह त्रिभुज जिसकी समान भुजा 8 सेमी. तथा तीसरी भुजा 4 सेमी. हो।
(iii) समकोण त्रिभुज जिसकी समकोण बनाने वाली भुजाओं की माप क्रमश: 20 सेमी. एवं 15 सेमी. है।
हल:
(i) यदि समबाहु त्रिभुज की भुजा a हो तो
परिमाप = 3a
3a = 60
a = \(\frac{60}{3}\) = 20 सेमी.

समबाहु त्रिभुज का क्षेत्रफल = \(\frac{a^{2} \cdot \sqrt{3}}{4}\) वर्ग सेमी.
= \(\frac{(20)^{2} \cdot \sqrt{3}}{4}\)
= \(\frac{20 \times 20 . \sqrt{3}}{4}\)
= 5 × 20 × √3
= 100√3 वर्ग सेमी.

(ii) माना कि a = 8 सेमी., b = 4 सेमी.
अतः समद्विबाहु त्रिभुज का क्षेत्रफल

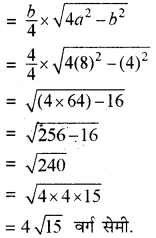
(iii) माना a = 20 सेमी. व b = 15 सेमी.
समकोण त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) × a × b
= \(\frac{1}{2}\) × 20 × 15
= 10 × 15
= 150 वर्ग सेमी.

प्रश्न 4.
किसी त्रिभुज का परिमाप 40 सेमी. है। यदि इसकी दो भुजाएँ क्रमशः 8 सेमी. एवं 15 सेमी. हों, तो इसका क्षेत्रफल ज्ञात कीजिए एवं सबसे लम्बी भुजा पर शीर्ष से डाले गए लम्ब की लम्बाई ज्ञात कीजिए।
हल:
त्रिभुज का परिमाप = a + b + c = 40 सेमी.

माना a = 8 सेमी., b = 15 सेमी.
8 + 15 + c = 40
c = 40 - 23
c = 17

त्रिभुज का अर्द्ध-परिमाप (s)
= \(\frac{a+b+c}{2}=\frac{40}{2}\) = 20 सेमी.

त्रिभुज का क्षेत्रफल
= \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{20(20-8)(20-15)(20-17)}\)
= \(\sqrt{20 \times 12 \times 5 \times 3}\)
= \(\sqrt{3600}\)
= \(\sqrt{60 \times 60}\)
= 60 वर्ग सेमी.

सबसे लम्बी भुजा BC = a = 17 सेमी. है।
शीर्ष से डाले लम्ब AD की लम्बाई

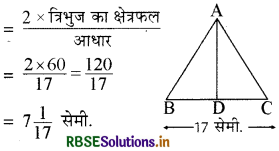
प्रश्न 5.
समबाहु त्रिभुज की ऊँचाई ज्ञात कीजिए जिसकी एक भुजा 2a है।
हल:
समबाहु त्रिभुज की एक भुजा = 2a

प्रश्न 6.
एक त्रिभुजाकार खेत की भुजाएँ 20 मी., 51 मी. एवं 37 मी. हैं। 2 × 3 वर्ग मीटर माप की कितनी क्यारियाँ इस खेत में बनाई जा सकती हैं ?
हल:
माना त्रिभुजाकार खेत की भुजाएँ a = 20 मी., b = 51 मी., C = 37 मी. हैं।

खेत का अर्द्ध-परिमाप (s)
= \(\frac{a+b+c}{2}=\frac{20+51+37}{2}\)
= \(\frac{108}{2}\) = 54 मी.

त्रिभुज का क्षेत्रफल

एक क्यारी का क्षेत्रफल = 2 × 3 = 6 वर्ग मीटर खेत में क्यारियों की संख्या

प्रश्न 7.
एक त्रिभुजाकार भूखण्ड (plot) की | भुजाओं का अनुपात 3 :5 : 7 है और उसका परिमाप 300 m है। इस भूखण्ड का क्षेत्रफल ज्ञात कीजिए।
हल:
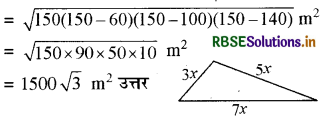
मान लीजिए भुजाएँ (मीटरों में) 3x, 5x और 7x हैं।
तब, हम जानते हैं कि 3x + 5x + 7x = 300 (त्रिभुज का परिमाप)
इसलिए, 15x = 300 है, जिससे x = 20 प्राप्त होता
इसलिए, त्रिभुज की भुजाएँ 3 × 20 m, 5 × 20 m और 7 × 20 m हैं।
अर्थात् ये भुजाएँ 60 m, 100 m और 140 m हैं ।
अब, s = \(\frac{60+100+140}{2}\) m = 150 m

इसलिए, क्षेत्रफल