RBSE Class 9 Maths Important Questions Chapter 11 Constructions

Rajasthan Board RBSE Class 9 Maths Important Questions Chapter 11 Constructions Important Questions and Answers.

RBSE Class 9 Maths Chapter 11 Important Questions Constructions

I. Multiple Choice Questions :
Choose the correct answer from the given four options.

Question 1.
If the lengths of two sides of an isosceles triangle are 4 cm and 10 cm, then the length of the third side is :
(a) 4 cm
(b) 10 cm
(c) 7 cm
(d) 14 cm
Answer:
(b) 10 cm

Question 2.
With the help of ruler and compass, it is possible to construct an angle of:
(a) 35°
(b) 40°
(c) 37.5°
(d) 47.5°
Answer:
(c) 37.5°

 

Question 3.
The construction of a triangle ABC, given that BC = 6 cm, ∠B = 45° is not possible when the difference of AB and AC is equal to :
(a) 6.9 cm
(b) 5.2 cm
(c) 5.0 cm
(d) 4.0 cm
Answer:
(a) 6.9 cm

Question 4.
The construction of a triangle ABC, given that BC = 3 cm, ZC = 60° is possible when the difference ofAB andAC is equal to :
(a) 3.2 cm
(b) 3.1 cm
(c) 3 cm
(d) 2.8 cm
Answer:
(d) 2.8 cm

Question 5.
Which of the following angles cannot be constructed using ruler and compass only?
(a) 40°
(b) 120°
(c) 135°
(d) 37.5°
Answer:
(a) 40°

Question 6.
The construction of a ∆ABC in which AB = 6 cm, ∠A = 45° is possible when (BC + AC) is :
(a) 7 cm
(b) 5.8 cm
(c) 5 cm
(d) 4.9 cm
Answer:
(a) 7 cm

Question 7.
The construction of a ∆ABC in which AB = 7 cm, ∠A = 75° and possible when (BC - AC) is equal to :
(a) 7.5 cm
(b) 7 cm
(c) 8 cm
(d) 6.5 cm
Answer:
(d) 6.5 cm

Question 8.
Which of the following angles cannot be constructed using ruler and compass only?
(a) 22\(\frac{1^{\circ}}{2}\)
(b) 15°
(c) 52\(\frac{1^{\circ}}{2}\)
(d) 32\(\frac{1^{\circ}}{2}\)
Answer:
(d) 32\(\frac{1^{\circ}}{2}\)

Question 9.
A unique triangle cannot be constructed, if its:
(a) three angles are given.
(b) two angles, and one side is given.
(c) three sides are given.
(d) two sides and the included angle is given.
Answer:
(a) three angles are given.

II. Fill in the Blanks:

Question 1.
With the help of a ruler and a compass it is not possible to construct an angle of ___________. (40°/22.5°)
Answer:
40°

Question 2.
A perpendicular that divides a line segment into two equal parts is called its ___________.
Answer:
perpendicular bisector

Question 3.
When the sum of two adjacent angles is 180°, then they are called a ___________.
Answer:
linear pair

Question 4.
In a triangle, angle opposite to the longer side is ___________.
Answer:
larger

Question 5.
Sun of any two sides of a triangle is ___________ than the third side.
Answer:
greater

III. True/False:
State whether the following statements are True or False.

Question 1.
An angle of 37.5° can be constructed with the help of a ruler and a compass.
Answer:
True

Question 2.
An angle of 22.5° cannot be constructed with the help of a ruler and a compass.
Answer:
False

Question 3.
An angle of 62.5° cannot be constructed with the help of a ruler and a compass.
Answer:
True

Question 4.
An angle of 52.5° can be constructed with the help of a ruler and a compass.
Answer:
True

Question 5.
An angle of 42.5° can be constructed with the help of a ruler and a compass.
Answer:
False

Question 6.
A triangle ABC can be constructed in which ∠B = 60°, ∠C = 45° and AS + BC + AC = 12 cm
Answer:
True

IV. Very Short Answer Type Questions:

Question 1.
Can a ∆ABC be constructed, in which BC = 6 cm, ∠C = 30° and AC - AB = 4 cm.
Answer:
Yes, because the difference of any two sides of a triangle is always less than the third side.

Question 2.
Can an angle of 67.5° be constructed?
Answer:
Yes, because
67.5° = \(\frac{135^{\circ}}{2}=\frac{1}{2}\) (90°+ 45°)

V. Short Answer Type Questions:

Question 1.
Draw an exterior angle of a triangle. By using ruler and compass, bisect it.
Answer:

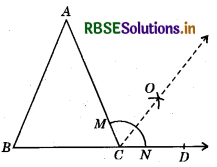
Steps of Construction :

1. Draw a ∆ABC. Extend BC to make an exterior angle ∠ACD.
2. Bisect angle ∠ACD → Taking C as centre and any suitable radius, draw an arc to intersect AC at M and CD, at N.
3. Taking M as centre and radius more than half of MN draw an arc.
4. Also taking N as centre, cut the previous arc at O.
5. Join CO.

Question 2.
Can a ∆ABC be constructed in which ∠B = 105°, ∠C = 90° and AB + BC + CA = 10 cm?
Answer:
It is given that :
AB + BC + CA = 10 cm
∠B = 105° and ∠C = 90°
Also, ∠A + ∠B + ∠C = 180°
⇒ ∠A + 105° + 90° = 180°
⇒ ∠A + 195° = 180°
⇒ ∠A = - 15° which is not possible as in ∆ABC, sum of two angles is more than 180°.
Thus, ∆ABC cannot be constructed.

Question 3.
Construct an equilateral triangle if its altitude is 6 cm. Give justification for your construction.
Answer:

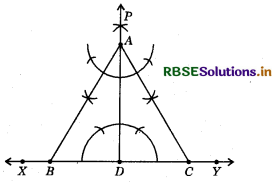
Draw a line XY. Take any point D on this line. Construct perpendicular PD on XY. Cut a line segment AD from PD equal to 6 cm. Make angles equal to 30° at A on both sides of AD, say ∠CAD and ∠BAD where B and C lie on XY. Then ABC is the required triangle.

Justification: Since ∠A = 30° + 30° = 60° and AD ⊥ BC, ∆ABC is an equilateral triangle with altitude AD = 6 cm.

Question 4.
Draw an acute-angled triangle ABC. Construct perpendicular bisectors of AB and BC intersecting each other at O. Measure OA, OB and OC. Are they equal?
Answer:
Steps of Construction :

1. Draw an acute-angled triangle ABC.
2. Taking B and A as centres and' radius more than BA, draw arcs on both sides of the line segment BA (to intersect each other).
3. Let these arcs intersect each other at D and E. Join DE.
4. Let DE intersect BA at the point M. Then line DME is the required bisector of BA.
5. Again, taking B and C as centres and radius more than \frac{1}{2}BC, draw arcs on both sides of the line segment BC (to intersect each other).
6. Let these arcs intersect each other at F and G. Join FG.
7. Let FG intersect BC at the point N. Then line FNG is the required bisector of BC.
8. Let the bisectors DME and FNG intersect each other at O.
   By measurement, OA = OB = OC = 3.8 cm

Question 5.
Construct a rhombus whose diagonals are 8 cm and 6 cm long. Measure the length of each side of the rhombus.
Answer:

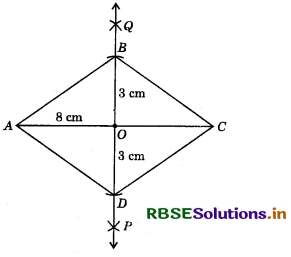
Steps of Construction:

1. Draw a line segment AC = 8 cm.
2. Draw the right bisector PQ of the line segment AC. Let O be the point of intersection of AC and PQ so that O is the mid-point of AC.
3. From OP, cut a line segment OD = 3 cm and .from OQ, cut a line segment OB = 3 cm.
   (∵ The other diagonal is 6 cm long and half of 6 cm is 3 cm.)
4. Join AD, DC, CB and AB, then ABCD is the required rhombus.
5. Measure the lengths of segments AB, BC, CD and DA; each is found to be 5 cm long.
   Justification: Right triangles AOB, BOC, COD and AOD are congruent to each other as ∠AOB = ∠BOC = ∠COD = ∠AOD = 90°; OA = OC = 4 cm and OB = OD 3 cm.
   (By SAS congruency criterion)

Question 6.
Construct ∆ABC in which BC = 6.8 cm, ∠B = 45° and ∠C = 45°. Construct angle bisector of ∠B and ∠C and let them intersect at point O. Measure angle BOC.
Answer:

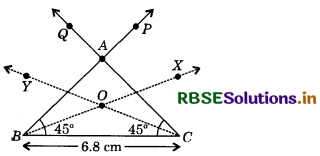
Steps of Construction :

1. Draw a line segment BC =6.8 cm.
2. Draw ∠PBC = 45° at point B and draw ∠QCB = 45° at point C.
3. Mark the point of intersection of ray BP and ray CQ at A.
4. Now, draw the angle bisectors of ∠ABC and ∠ACB, let them to intersect each other at point O. On measuring the ∠BOC, we get the value 135°

Question 7.
Construct an angle of 7\frac{1^{\circ}}{2} using compass and ruler only.
Answer:

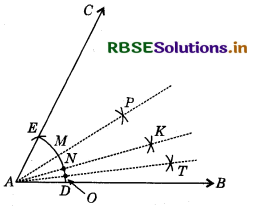
Steps of Construction:
Here, 7 \(\frac{1^{\circ}}{2}=\frac{60^{\circ}}{8}=\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times 60^{\circ}\),
so construct an angle of 7\(\frac{1^{\circ}}{2}\), first draw an angle of 60°, say ∠BOC and then bisect to get ∠BOP = 30°. Again bisect ∠BOP, to get ∠BOK = 15°, Further, bisect ∠BOK to get ∠BOT = 7\(\frac{1^{\circ}}{2}\).

Long Answer Type Questions:

Question 1.
Construct a triangle PQR such that ∠P = 90°, ∠Q = 60° and the perimeter of the triangle is 12 cm.
Answer:

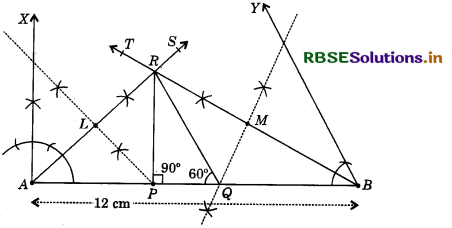
Steps of Construction:

1. Draw AB = 12 cm.
2. At A construct ∠BAS = \(\frac{1}{2}\) × 90° = 45° and at B construct ∠ABT = \(\frac{1}{2}\) × 60° = 30°.
3. Let AS and BT meet at R.
4. Draw perpendicular bisector of AR to meet AB at P.
5. Draw perpendicular bisector of BR to meet AB at Q.
6. Join RP and PQ. Then RPQ is the required triangle.

Question 2.
Construct a triangle ABC in which AB = 5.8 cm, BC + CA = 8.4 cm and ∠B = 60°. Also, justify the construction.
Answer:

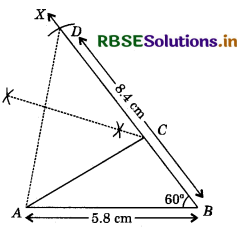
In order to construct the ∆ ABC we follow the following steps:

Steps of Construction:

1. Draw AB = 5.8 cm.
2. Draw ∠ABX = 60°
3. From ray BX, cut-off line segment BD = BC + CA = 8.4 cm.
4. Join AD.
5. Draw the perpendicular bisector of AD meeting BD at C.
6. Join AC to obtain the required triangle ABC.

Justification: Clearly, C lies on the perpendicular bisector of AD.
∴CA = CD
Now, BD = 8.4 cm
⇒ BC + CD = 8.4 cm .
⇒ BC + CA = 8.4 cm .
Hence, ∆ABC is the required triangle.

Question 3.
Construct a ∆ABC in which ∠B = 60°, ∠C = 75° and the perpendicular from the vertex A to the base BC is 5 cm.
Answer:

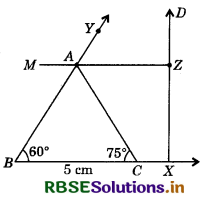
Steps of Construction :

1. Draw a ray BX.
2. Make an angle of 60° at the point BX of B such that ∠YBX = 60°.
3. Draw a perpendicular XD at X.
4. Cut-off XZ = 5 cm from XD.
5. Draw ZM parallel to XB that intersects BY at A.
6. Make an angle of 75° at point A downwards AZ which intersects BX at C.
   Thus, ∆ABC is the required triangle.