RBSE Class 9 Maths Important Questions Chapter 11 रचनाएँ

Rajasthan Board RBSE Class 9 Maths Important Questions Chapter 11 रचनाएँ Important Questions and Answers.

RBSE Class 9 Maths Chapter 11 Important Questions रचनाएँ

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
ज्यामितीय संरचना में ध्यान रखने योग्य बात है
(A) आकृति शुद्ध व स्वच्छ हो।
(B) रचना के पदों का शब्दों में वर्णन हो
(C) रेखायें गहरी पेंसिल से खींची गई हों
(D) उपर्युक्त सभी
उत्तरः
(D) उपर्युक्त सभी

प्रश्न 2.
75° के कोण की रचना के लिए किन दो कोणों को बनाना अनिवार्य है
(A) 90° व 60°
(B) 30° व 50°
(C) 60° व 30°
(D) 45° व 30°
उत्तरः
(A) 90° व 60°

प्रश्न 3.
जब दो सरल रेखाओं को एक तिर्यक सरल रेखा काटे और इस प्रकार बने संगत कोण बराबर हों तो वे रेखायें होंगी
(A) लम्बवत्
(B) समान्तर
(C) 60° का कोण बनाती हुई
(D) तिर्यक प्रतिच्छेदी
उत्तरः
(B) समान्तर

प्रश्न 4.
प्रत्येक त्रिभुज में कोणों की संख्या होती है
(A) दो
(B) तीन
(C) चार
(D) पांच
उत्तरः
(B) तीन

प्रश्न 5.
त्रिभुज के तीनों कोणों का योग होता है
(A) 260°
(B) 320°
(C) 180°
(D) 120°
उत्तरः
(C) 180°

प्रश्न 6.
किस स्थिति में त्रिभुज की रचना नहीं की जा सकती
(A) यदि तीनों कोण दिए हों
(B) तीन भुजाएँ दी हों
(C) दो कोण व एक भुजा दी हो
(D) दो भुजाएँ व उनके मध्य का कोण दिया हो
उत्तरः
(A) यदि तीनों कोण दिए हों

रिक्त स्थानों की पूर्ति करो

प्रश्न 1.
एक त्रिभुज की रचना की जा सकती है जिसका परिमाप एवं ....................... आधार कोण दिए गए हों।
उत्तरः
दो

प्रश्न 2.
एक त्रिभुज की रचना की जा सकती है जिसमें आधार, एक आधार कोण तथा अन्य दो भुजाओं का .......................... दिया गया हो।
उत्तरः
अन्तर या योग

प्रश्न 3.
किसी त्रिभुज की रचना नहीं की जा सकती जिसमें केवल .............................. दिए हों।
उत्तरः
तीन कोण

प्रश्न 4.
ऐसे त्रिभुज की रचना की जा सकती है जिसकी दो भुजाएँ और उनमें से एक सामने का ........................... दिया गया हो।
उत्तरः
कोण

प्रश्न 5.
समकोण त्रिभुज की रचना करने के लिए कर्ण एवं ................................ भुजा दी गई हो।
उत्तरः
एक

सत्य/असत्य-निम्नलिखित कथनों के लिए सत्य अथवा असत्य लिखिए.

प्रश्न 1.
परकार एवं पटरी की सहायता से 37.5° के कोण की रचना नहीं की जा सकती।
उत्तर:
असत्य

प्रश्न 2.
परकार एवं पटरी की सहायता से 22.5° के कोण की रचना की जा सकती है।
उत्तर:
सत्य

प्रश्न 3.
एक त्रिभुज POR का निर्माण नहीं किया जा सकता जिसमें PQ = 3 सेमी., ∠Q = 90° और OR - RP = 2.8 सेमी.।
उत्तर:
असत्य

प्रश्न 4.
एक त्रिभुज ABC की रचना की जा सकती है जबकि ∠B = 60°, ∠C = 45° और AB + BC + AC = 12 सेमी.।
उत्तर:
सत्य

प्रश्न 5.
एक कोण 42.5° की परकार व पटरी की सहायता से रचना की जा सकती है।
उत्तर:
असत्य

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
75° = 60° + ...........
उत्तर:
15°

प्रश्न 2.

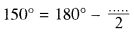
उत्तर:
60°

प्रश्न 3.
135° के कोण की रचना के लिए कौनसे दो कोणों का अर्द्धक होगा?
उत्तर:
180° व 90°

प्रश्न 4.
किसी त्रिभुज में कितने अवयव होते हैं ?
उत्तर:
प्रत्येक त्रिभुज में छः अवयव होते हैंतीन भुजायें व तीन कोण।

प्रश्न 5.
त्रिभुज की रचना करने के लिए कम से कम कितने स्वतन्त्र अवयव ज्ञात होने आवश्यक हैं ?
उत्तर:
तीन।

प्रश्न 6.
यदि किसी त्रिभुज की रचना हेतु दो भुजायें और इनमें से एक के सामने का न्यूनकोण दिया हो तो क्या होता है?
उत्तर:
अभीष्ट त्रिभुज की संदिग्ध स्थिति उत्पन्न हो जाती है। क्योंकि इस स्थिति में दो त्रिभुज बन सकते हैं और अभीष्ट त्रिभुज निश्चित नहीं किया जा सकता।

लघूत्तरात्मक प्रश्न:

प्रश्न 1.
एक दी गई किरण के प्रारम्भिक बिन्दु पर 60° के कोण की रचना कीजिए।
हल:
रचना के चरण:
(1) A को केन्द्र मानकर और कोई त्रिज्या लेकर एक वृत्त का चाप खींचिए, जो AB को मान लीजिए एक बिन्दु D पर प्रतिच्छेद करता है।
(2) D को केन्द्र मानकर और उसी त्रिज्या, जो पहले ली गई थी, से एक चाप खींचिए, जो चरण 1 में खींचे गए चाप को बिन्दु E पर प्रतिच्छेद करता है।
(3) E से जाने वाली किरण AC खींचिए। [देखिए आकृति]

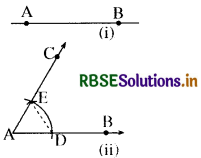
तब ∠CAB ही 60° का अभीष्ट कोण है। DE को मिलाइए।
तब, AE = AD = DE (रचना से)
अतः, ∆ EAD एक समबाहु त्रिभुज है और ∠EAD, जो कि ∠CAB के बराबर है, 60° का है।

प्रश्न 2.
रेखाखण्ड AB = 10 सेमी. खींचिए। इसका समद्विभाजन कीजिए तथा दोनों रेखाखण्डों को मापकर उत्तर की जाँच कीजिए।
हल:
रचना:
(1) एक रेखाखण्ड AB = 10 सेमी. खींचो।

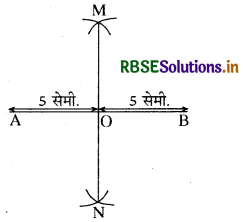
(2) A और B को केन्द्र मानकर, रेखाखण्ड के आधे से अधिक की त्रिज्या से AB के दोनों ओर चाप खींचो, जो एक-दूसरे को क्रमश: M और N बिन्दुओं पर काटें।
(3) MN को मिलाओ जो AB को बिन्दु 0 पर मिलती है। बिन्दु 0 रेखा AB को समद्विभाजित करता है।
अत: OA = OB
मापने पर OA = 5 सेमी. = OB

प्रश्न 3.
120° के कोण की रचना कीजिए। इस कोण की समद्विभाजक रेखा खींचिये। दोनों कोणों को मापकर उत्तर की जांच कीजिए।
हल:
रचना:
(1) रेखाखण्ड AB पर बिन्दु 0 को केन्द्र मानकर किसी भी त्रिज्या से चाप खींचिए, जो AB को P पर काटे।

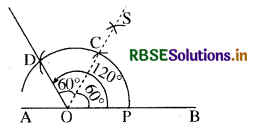
(2) P को केन्द्र मानकर उसी त्रिज्या से क्रमश: दो चाप खींचिए जो पहले चाप को क्रमश: C व D पर काटें। OD को मिलाइये। इस प्रकार ∠BOD = 120° बना।
(3) कोण DOP के आधे से अधिक की त्रिज्या से DP के दोनों ओर से चाप काटें जो बिन्दु S पर मिलते हैं। अब SO को मिलायें। यह कोण DOP की समद्विभाजक रेखा है।
मापने पर-∠POC = 60° = ∠COD तथा ∠POC + ∠COD = 120°
अतः उत्तर सही है।

प्रश्न 4.
चाँदे की सहायता से 40° का कोण बनाइये। इसी के बराबर कोण की रचना परकार तथा मापनी की सहायता से कीजिए।
हल:
रचना:
(1) एक रेखा DO खींचिये। इस पर चांदे की सहायता से ∠PDO = 40° का कोण बनाइए।

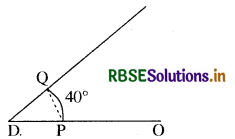
(2) D को केन्द्र मानकर एक उचित त्रिज्या का चाप खींचिये जो कोण की भुजाओं को P और Q पर काटे।
(3) अब एक रेखा AB खींचिए। इस पर किसी बिन्दु 0 को केन्द्र मानकर DP के बराबर त्रिज्या से चाप खींचिए जो AB को R पर काटे। R को केन्द्र मानकर PQ की त्रिज्या के बराबर चाप खींचिए जो पूर्व चाप को S पर काटे। OS को मिलाइये।

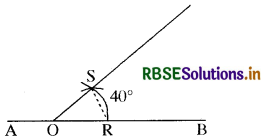
∠BOS = 40° प्राप्त होगा।

प्रश्न 5.
एक 6 सेमी. की रेखा खींचिये, इसके बाहर किसी बिन्दु P से इस पर लम्ब खींचिये।
हल:
रचना:
(1) AB = 6 सेमी. खींचिये।
(2) बिन्दु P को केन्द्र मानकर, बिन्दु P से AB तक की दूरी से अधिक की उचित त्रिज्या लेकर एक चाप खींचिये जो AB को क्रमश: C और D बिन्दुओं पर काटे।

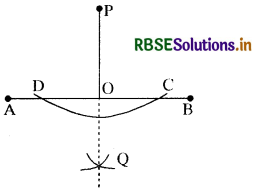
(3) C और D को क्रमशः केन्द्र मानकर CD के आधे से अधिक उचित त्रिज्या से दो चाप AB के नीचे की ओर खींचें जो एक-दूसरे को Q पर काटें।
(4) PQ को मिलाइये। यह AB को जहां मिले वहां 0 लिखिये । PO अभीष्ट लम्ब है।

प्रश्न 6.
परकार एवं पटरी की सहायता से 150° के कोण की रचना कीजिए।
हल:
150° के कोण की रचना-
150° = \(\frac{180^{\circ}+120^{\circ}}{2}\)

(1) एक रेखाखण्ड AB किसी भी माप का खींचिए।

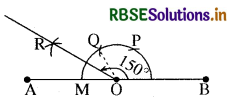
(2) इस पर किसी बिन्दु 0 से परकार व पटरी द्वारा 60° व 120° के लिए दो चाप क्रमशः P व Q काटिये।
(3) ∠QOM का अर्द्धक OR खींचिये। इस प्रकार ∠BOR = 150° प्राप्त होगा।

प्रश्न 7.
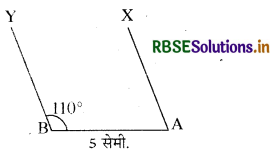
एक सरल रेखा AB = 5 सेमी. खींचिए। इस पर ∠YBA = 110° का बनाइए। इसके A बिन्दु पर YB के समान्तर सरल रेखा खींचिए। .
हल:
रचना-AB = 5 सेमी. का आधार खींचो। बिन्दु B पर YBA = 110° का कोण बनाया। बिन्दु A पर 70° का कोण बनाओ। यह रेखा YB के समान्तर होगी।

प्रश्न 8.
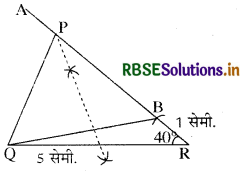
त्रिभुज PQR की रचना कीजिए जिसमें QR = 5 सेमी., ∠R = 40° एवं PR - PQ = 1 सेमी.।
हल:
रचना-आधार QR = 5 सेमी. का खींचो। बिन्दु R पर ∠ORA = 40° का बनाओ। AR से 1 सेमी. काटो। यह बिन्दु B है। B को Q से मिलाओ तथा BQ का समद्विभाजन करो। यह AR को P पर मिलता है। P को Q से मिलाओ। इस प्रकार अभीष्ट त्रिभुज PQR प्राप्त होगा।

निबन्धात्मक प्रश्न

प्रश्न 1.
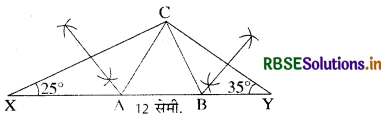
त्रिभुज ABC की रचना कीजिए जिसकी परिमिति 12 सेमी. एवं आधार के कोण 50° और 70° हों।
हल:
रचना-आधार XY = 12 सेमी. का खींचो तथा इसके बिन्दु X व Y पर क्रमश: ∠A व ∠B के अर्द्धक कोण क्रमश: 25° व 35° के बनाइए। ये परस्पर C बिन्दु पर मिलते हैं। CX व CY के अर्द्धक खींचो जो आधार XY को A व B बिन्दु पर काटते हैं, C को B व A से मिलाकर अभीष्ट ∆ABC प्राप्त करो।

प्रश्न 2.
त्रिभुज ARC' की रचना कीजिए, जबकि आधार BC = 5 सेमी., ∠ABC = 60° एवं AB + AC = 8 सेमी. है।
हल:
दी गई मापों से त्रिभुज का कच्चा चित्र खींचकर उसमें दी गई मापें अंकित कीजिए। BA को बिन्दु D तक इस प्रकार बढ़ाइये कि AC = AD हो । इस प्रकार BD = BA + AC, D को C बिन्दु से मिलाइए।
रचना:
(1) BC = 5 सेमी. खींचिए।
(2) बिन्दु B पर 60° का कोण YBC पटरी व परकार से बनाइए।
(3) BY में से, (BA + AC) के बराबर दूरी BD = 8 सेमी. काटिए।
(4) D को C से मिलाइए। DC का लम्ब समद्विभाजक खींचिए, जो BD को A बिन्दु पर काटे। A को C से मिलाइए।

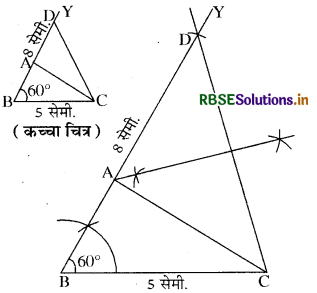
इस प्रकार ABC अभीष्ट त्रिभुज है। जिसमें BA + AC = 7 सेमी. है।

प्रश्न 3.
एक त्रिभुज की रचना कीजिए जिसका परिमाप तथा दोनों आधार कोण दिए हों। आधार के कोण ∠B तथा ∠C और (BC + CA + AB) दिए हैं। आपको त्रिभुज ABC की रचना करनी है।
हल:
रचना के चरण
(1) BC + CA + AB के बराबर एक रेखाखण्ड XY, खींचिए।
(2) ∠LXY कोण B के बराबर तथा ∠MYX कोण C के बराबर बनाइए।

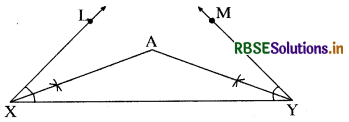
(3) ∠LXY तथा ∠MYX को समद्विभाजित कीजिए। माना ये समद्विभाजक एक बिन्दु A पर प्रतिच्छेद करते हैं [देखिए आकृति] ।
(4) AX का लम्ब समद्विभाजक PQ तथा AY का लम्ब समद्विभाजक RS खींचिए।
(5) मान लीजिए कि PQ, XY को बिन्दु B पर तथा RS, XY को बिन्दु C पर प्रतिच्छेद करता है। AB और AC को मिलाइए [देखिए आकृति] ।
तब ABC अभीष्ट त्रिभुज है। रचना के समर्थन के लिए, आप पाते हैं कि B, AX के लम्ब समद्विभाजक पर स्थित है।

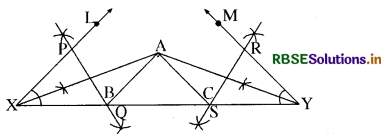
अत: XB = AB है। इसी प्रकार, CY = AC है। इससे प्राप्त होता है-
BC + CA + AB = BC + XB + CY = XY
पुनः ∠BAX = ∠AXB
(क्योंकि ∆AXB में AB = XB)
तथा ∠ABC = ZBAX + ZAXB
= 2 ∠AXB = ∠LXY
इसी प्रकार ∠ACB = ∠MYX जैसा चाहिए था।

प्रश्न 4.
एक त्रिभुज ABC की रचना कीजिए जिसमें ∠B = 60°, ∠C = 45° और AB + BC + CA = 11 cm है।
हल:
रचना के चरण
(1) एक रेखाखण्ड PQ = 11 cm है (= AB + BC + CA) खींचिए।
(2) P पर 60° का कोण तथा Q पर 45° का कोण बनाइए।
(3) इन कोणों को समद्विभाजित कीजिए। मान लीजिए कि ये समद्विभाजक एक बिन्दु A पर प्रतिच्छेद करते हैं।
(4) AP का लम्ब समद्विभाजक DE खींचिए जो PQ को बिन्दु B पर प्रतिच्छेद करता है और AQ का लम्ब समद्विभाजक खींचिए जो PQ को बिन्दु C पर प्रतिच्छेद करता है।

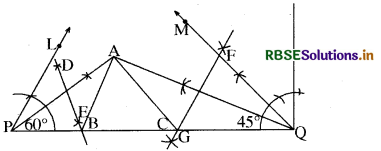
(5) AB को और AC को मिलाइए (देखिए आकृति)।
तब, ABC अभीष्ट त्रिभुज है।