RBSE Class 9 Maths Important Questions Chapter 10 Circles

Rajasthan Board RBSE Class 9 Maths Important Questions Chapter 10 Circles Important Questions and Answers.

RBSE Class 9 Maths Chapter 10 Important Questions Circles

I. Multiple Choice Questions :
Choose the correct from the given four options.

Question 1.
In the given figure, AB is a chord of a cirde with centre O and AB is produced to C such that BC = OB. Also, CO is joined and produced to meet the circle in D. If ∠ACD = 25°, then ∠AOD = ?

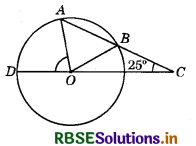
(a) 50°
(b) 75°
(c) 90°
(d) 100°
Answer:
(b) 75°

Question 2.
In the given figure, BOC is a diameter of a circle with centre O. If ∠BCA = 30°, then ∠CDA = ?

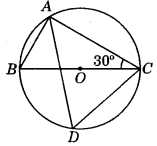
(a) 30°
(b) 45°
(c) 60°
(d) 50°
Answer:
(c) 60°

Question 3.
In the given figure, O is the centre of a circle and ∠AOC = 120°, Then ∠BDC = ?

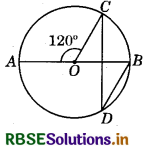
(a) 60°
(b) 45°
(c) 30°
(d) 15°
Answer:
(c) 30°

Question 4.
In the adjoining figure, O is the centre of the circle. If OA = 5 cm, AB = 8 cm and OD ⊥ AB, then length of CD is equal to :

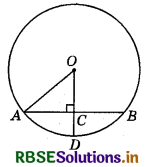
(a) 2 cm
(b) 3 cm
(c) 4 cm
(d) 5 cm
Answer:
(a) 2 cm

Question 5.
AD is a diameter of a circle and AB is a chord. If AD = 34 cm and AB = 30 cm, then the distance of AB from the centre of circle is :
(a) 17cm
(b) 15cm
(c) 4cm
(d) 8cm
Answer:
(d) 8cm

Question 6.
The circumference of a circle must be:
(a) a positive real number
(b) a whole number
(c) a natural number
(d) an integer
Answer:
(a) a positive real number

Question 7.
If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is :
(a) 6 cm
(b) 8 cm
(c) 10 cm
(d) 12 cm
Answer:
(c) 10 cm

Question 8.
In the adjoining figure, O is the centre of the circle. If ∠OAB = 40°, then ∠ACB is equal to :

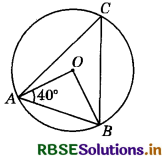
(a) 50°
(b) 40°
(c) 60°
(d) 70°
Answer:
(a) 50°

Question 9.
ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140°, then ∠BAC is equal to :
(a) 80°
(b) 50°
(c) 40°
(d) 30°
Answer:
(b) 50°

Question 10.
In the adjoining figure, if ∠DAB = 60° and ∠ABD = 50°, then ∠ACB is equal to :

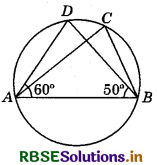
(a) 60°
(b) 50°
(c) 70°
(d) 80°
Answer:
(c) 70°

Question 11.
In the adjoining figure, 0 is the centre of the circle. If ∠ABC = 20°, then ∠AOC is equal to :

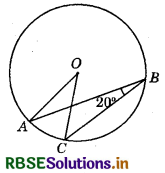
(a) 20°
(b) 40°
(c) 60°
(d) 10°
Answer:
(b) 40°

Question 12.
In the adjoining figure, O is the centre of the circle. If ∠AOB = 90°and ∠ABC = 30°, then ∠CAO is equal to :

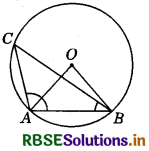
(a) 30°
(b) 45°
(c) 90°
(d) 60°
Answer:
(d) 60°

Question 13.
In the adjoining figure, O is the centre of the circle. If ∠BAO = 60° then ∠ADC is equal to :

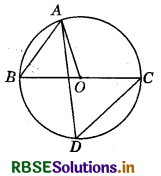
(a) 30°
(b) 45°
(c) 60°
(d) 120°
Answer:
(c) 60°

Question 14.
In the given figure, O is the centre of a circle in which ∠OAB = 20° and ∠OCB = 50°. Then, ∠AOC = ?

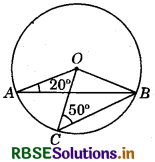
(a) 50°
(b) 70°
(c) 20°
(d) 60°
Answer:
(d) 60°

Question 15.
In the given figure, AOB is a diameter and ABCD is a cyclic quadrilateral. If ∠ADC = 120°, then ∠BAC = ?

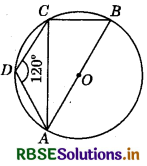
(a) 60°
(b) 30°
(c) 20°
(d) 45°
Answer:
(b) 30°

Question 16.
In the given figure, ABCD is a cyclic quadrilateral in which AB ∥ DC and ∠BAD = 100°. Then ∠ABC = ?

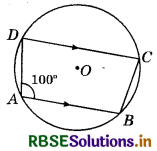
(a) 80°
(b) 100°
(c) 50°
(d) 40°
Answer:
(b) 100°

Question 17.
In the adjoining figure, sides AB and AD of quadrilateral ABCD are produced to E and F respectively. If ∠CBE = 100°, then ∠CDF =?

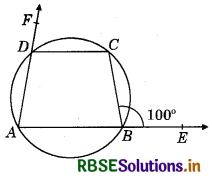
(a) 100°
(b) 80°
(c) 130°
(d) 90°
Answer:
(b) 80°

Question 18.
In the given figure, ABCD is a cyclic quadrilateral in which BC = CD and ∠CBD = 35°. Then ∠BAD=?

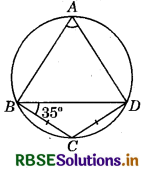
(a) 65°
(b) 70°
(c) 110°
(d) 90°
Answer:
(b) 70°

II. Fill in the Blanks:

Question 1.
The region between an arc and the two radii, joining the centre to the end points of the arc is called __________
Answer:
sector

Question 2.
If OA = 5 cm, AB = 8 cm and OD is perpendicular to AB in the given figure, then CD is equal to __________. (O is the centre of the circle)

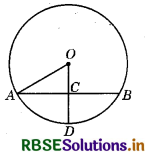
Answer:
2 cm

Question 3.
In the figure, if ∠ABE = 65°, then the value of ∠ADC will be __________.

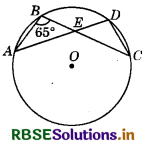
Answer:
65°

Question 4.
In the figure, if ∠ABC = 20°, then ∠AOC is equal to __________. (Here O is the centre of the circle)

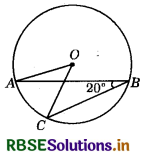
Answer:
40°

Question 5.
In the figure, PQRS is a quadrilateral. If ∠P = 180°, then ∠R is __________

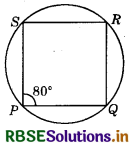
Answer:
100°

III. True/False :
State whether the following statements are True or False.

Question 1.
Line segment joining the centre to any point on the circle is a radius of the circle.
Answer:
True

Question 2.
If a circle is divided into three equal arcs, each is a major arc.
Answer:
False

Question 3.
Every circle has unique centre and it lies inside the circle.
Answer:
True

Question 4.
Angles in the same segment of a circle are equal.
Answer:
True

Question 5.
Sector is the region between the chord and its corresponding arc.
Answer:
False

Question 6.
Length of all radii of a circle is same.
Answer:
True

Question 7.
The length of tangents drawn from an external point to a circle are equal.
Answer:
True

IV. Match the Columns :

Question 1.
Match the column I with the column II.

Column I	Column II
(1) Distance around the circle.	(i) Circumcircle
(2) The point that has same distance from any point on the circumference.	(ii) Chord
(3) The region between a chord and either of its arcs.	(iii) Circumference
(4) A line joining two points on a circle.	(iv) Centre
(5) The circle that passes through the vertices of a plane figure.	(v) Segment

Answer:

Column I	Column II
(1) Distance around the circle.	(iii) Circumference
(2) The point that has same distance from any point on the circumference.	(iv) Centre
(3) The region between a chord and either of its arcs.	(v) Segment
(4) A line joining two points on a circle.	(ii) Chord
(5) The circle that passes through the vertices of a plane figure.	(i) Circumcircle

V. Very Short Answer Type Questions :

Question 1.
A chord of length 12 cm of a circle is at a distance of 8 cm from its centre. What is the radius of the circle?
Answer:
AB is a chord of a circle of radius r.

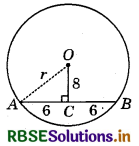
OC ⊥ AB ⇒ OC = 8
Also AC = CB
(∵ Perpendicular from the centre bisects the chord)
∴ AC = CB = \(\frac{12}{2}\) = 6 cm

In right-angled triangle OAC, we can write :
r² = 8² + 6² = 64 + 36 = 100
⇒ r = \(\sqrt{100}\) = 10 cm
∴ Radius of circle = 10 cm.

Question 2.
Three chords AB, CD and EF of a circle are respectively 3 cm, 3.5 cm and 3.8 cm away from the centre. Arrange the chords in ascending order of length.
Answer:
We know that of any two chords of a circle, one which is larger is nearer to the centre.
∴ EF is farthest from the centre and is the shortest chord.

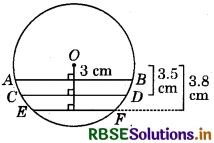
Similarly, chord AB is nearest to the centre and is the longest chord.
∴ We can say that AB > CD > EF

Question 3.
How many points are required to determine a unique circle?
Answer:
3 non-collinear points.

Question 4.
In the following figure, ∠CAB = 40°, ∠AKB = 105°. Find the measure of ∠KCD.

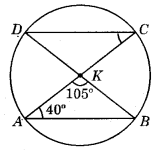
Answer:
∠BDC = ∠BAC = 40° (Angles in the same segment)
Also, ∠DKC = ∠AKB = 105° (Vertically opposite angles)
Now, in ΔDKC,
∠KDC + ∠DKC + ∠KCD = 180 (Angle sum property of a triangle)
⇒ 40 + 105 + ∠KCD = 180°
⇒ ∠KCD = 180° - 145° = 35°
Hence, ∠KCD = 35°

VI. Short Answer Type Questions :

Question 1.
In the figure, ∠ABD = 70°, ∠ADB = 30°. Find ∠BCD.
Answer:
In ΔABD,
∠A + ∠ABD + ∠ADB = 180°
(Angle sum property of a triangle)
⇒ ∠A + 70° + 30° = 180°
⇒ ∠A + 100° = 180°
⇒ ∠A = 180° - 100° = 80°
i.e., ∠A = 80°

∠A + ∠C = 180°
⇒ 80°+ ∠C = 180°
⇒ ∠C = 180° - 80° = 100°
Hence ∠BCD = 100°

Question 2.
In the figure, two concentric circles with centre O are given, OM ⊥ PS. If PS = 20 cm and QR = 15 cm, then find PQ.

Answer:
M is the mid-point of QR as well as PS as perpendicular from the centre bisects the chord.
∴ PM = \(\frac{1}{2}\)PS ⇒ PM = \(\frac{1}{2}\) × 20 = 10 cm
QM = \(\frac{1}{2}\) × QR ⇒ QM = \(\frac{1}{2}\) × 15 = 7.5 cm
∴ PQ = PM - QM = 10 - 7.5 = 2.5 cm

Question 3.
If BM and CN are the perpendiculars drawn on the sides AC and AB of ΔABC, then prove that the points B, C, M and N are concyclic.

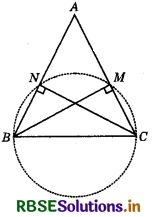
Answer:
Given: In ΔABC, BM ⊥ AC and CN ⊥ AB
To prove: Points B, C, M and N are concyclic.
Construction: Draw a circle passing through the points B, C, M and N.
Suppose, we consider BC as a diameter of the circle. Also, we know that, BC subtends an angle of 90° to the circle.
So the points M and N should be on a circle.
Hence, points B, C, M and N are concyclic.
Hence proved.

Question 4.
Prove that the circle described on any one of equal sides of an isosceles triangle as diameter bisects the base.
Answer:
Given : An isosceles ΔABC in which AB = AC.

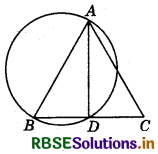
The circle drawn on AB as diameter intersects the base BC of ΔABC at the point D. We need to prove that D is mid-point of BC.
As AB is a diameter, ∠ADB = 90° (Angle in a semicircle)
⇒ AD ⊥ BC
In ΔABD and ΔACD AB = AC
AD = AD
∠ADB = ∠ADC
∴ ΔABD ≅ ΔACD
∴ BD = DC

Question 5.
In the given figure, ABCD is a cyclic quadrilateral, in which AC and BD are its diagonals. If ∠DBC = 60° and ∠BAC = 30°, then find ∠BCD.

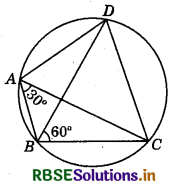
Answer:
Given : ABCD is a cyclic quadrilateral, in which AC and BD are its diagonals. Also, ∠DBC = 60° and ∠BAC = 30°
∴ ∠DBC = ∠CAD = 60° ....................(1)
(angles in the same segment)

Also, ∠BAD = ∠BAC + ∠CAD
= 30° + 60° = 90° ................(2) [From equation (1)]
Now, ∠BAD + ∠BCD = 180° (∵ ABCD is a cyclic quadrilateral.)
⇒ 90° + ∠BCD = 180° [From equation (2)]
⇒ ∠BCD = 90°

Question 6.
If a line segment joining mid-points of two chords of a circle passes through the centre of the circle. Prove that the two chords are parallel.
Answer:
Given : AB and CD are two chords of a circle, whose centre is O and PQ is a diameter bisecting the chords AB and CD at L and M, respectively and the diameter PQ passes through the centre O of the circle.

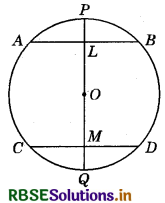
To prove : AB ∥ CD Proof: Since, L is the mid-point of AB.
∴ OL ⊥ AB (Since, the line joining the centre of a circle to the mid-point of a chord is perpendicular to the chord.)
∴ ∠ALO = 90°
Similarly, OM ⊥ CD
∴ ∠OMD = 90° ..............(2)

From equations (1) and (2), we get:
∠ALO = ∠OMD (Each 90°)
But these are alternate angles.
So, AB ∥ CD.
Hence proved.

Question 7.
In the given figure, AOB is a diameter of the circle and C, D and E are any three points on the semi-circle. Find the value of ∠ACD + ∠BED.

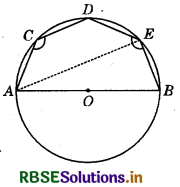
Answer:
Since, ACDE is a cyclic quadrilateral.
∴ ∠ACD + ∠AED = 180° ...............(1)
(v Sum of opposite angles of a cyclic quadrilateral is 180°.) .
Also, ∠AEB = 90° (Angle in semicircle) .................(2)

On adding equations (1) and (2), we get:
∠ACD + (∠AED + ∠AEB) = 180° + 90°
⇒ ∠ACD + ∠BED = 270°
Hence, the value of ∠ACD + ∠BED = 270°

Question 8.
In the figure P is the centre of the circle. Prove that: ∠XPZ = 2 (∠XZY + ∠YXZ)

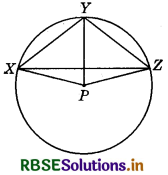
Answer:
Given : P is the centre of the given circle.
To prove : ∠XPZ = 2(∠XZY + ∠YXZ)
Proof: Since, angle subtended by an arc at the centre is double of the angle subtended by it at any point on the remaining part of the circle.
So, ∠XPY = 2 ∠XZY .............(1)
Similarly, ∠YPZ = 2∠YXZ ..............(2)

On adding equations (1) and (2), we get:
∠XPY + ∠YPZ = 2∠XZY + 2∠YXZ
⇒ ∠XPZ = 2(∠XZY + ∠YXZ)
Hence proved.

Question 9.
A circle has radius √2 cm. It is divided into two segments by a chord of length 2 cm. Prove that the angle subtended by the chord at a point in major segment is 45°.

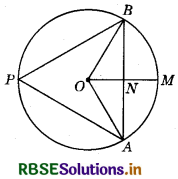
Answer:
Given : A circle having centre O.
Construction : A chord of a circle AB = 2 cm, which is divided by the line OM into two equal segments.
To prove : ∠APB = 45°.
Proof : Here, AN = NB = 1 cm
and OA = OB = √2 cm

In ΔONB, OB² = ON² + NB²
⇒ (√2)² = ON² + (1)²
⇒ ON² = 2 - 1 = 1
⇒ ON = 1

∴ ΔONB is an isosceles triangle.
∵ ∠ONB = 90° (Since, ON is the perpendicular bisector of the chord AS.)
∴ ∠NOB = ∠NBO = 45°
∠AON = 45°
∠AOB = ∠AON + ∠NOB = 45° + 45° = 90°
∠APB= \(\frac{1}{2}\)∠AOB
(Since, the angle subtended by an arc at the centre is twice the angle subtended by it at any point on the remaining part of the circle.)
∠APB = \(\frac{1}{2}\) × 90° = 45°
Hence Proved

VII. Long Answer Type Questions :

Question 1.
In the adjoining figure, O is the centre of the cirlce. If ∠SPQ = 45° and ∠POT = 150°, find the measures of :

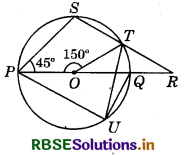
(i) ∠PST
(ii) ∠PUT
(iii) ∠QTR
(iv) ∠QRT
Answer:
(i) Reflex ∠POT = 360° - 150° = 210°
∴ ∠PST = \(\frac{1}{2}\) of reflex ∠POT
(∵ Angle subtended by major arc PUT at the centre = Double the angle subtended by it at any point on the remaining part of circle.)
⇒ ∠PST = \(\frac{1}{2}\) × 210° = 105°. 

(ii) As the sum of opposite angles of a cyclic quadrilateral is 180° and PSTO is cyclic quadrilateral.
∠PUT + ∠PST = 180°
⇒ ∠PUT + 105° = 180°
⇒ ∠PUT =75°

(iii) As an exterior angle of a cyclic quadrilateral = Interior opposite angle.
∠QTR = ∠SPQ
⇒ ∠QTR = 45° (As ∠SPQ = 45°, given)

(iv) ∠TQR = ∠PST (Exterior angle of cyclic quad. = Interior opp. ∠)
∠TQR = 105° [∵ ∠PST = 105° from part (i)]
∴ ∠QRT = 180° - (45° + 105°) (Sum of angles of a triangle = 180°)
⇒ ∠QRT = 30°.

Question 2.
Three STD booths situated at A, B and C in the figure are operated by handicapped persons. These three booths are equidistant from each other as shown in the figure.

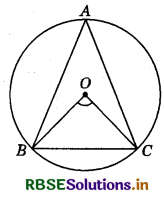
(i) Find ∠BAC
(ii) Find ∠BOC
(iii) Do you think employment provided to handicapped persons is important for the development of a society?
Answer:
Here, A, B and C represent three STD booths.
(i) Given: A, B and C are equidistant from each other.
∴ AB = BC = CA.
⇒ ΔABC is an equilateral triangle.
Hence, ∠BAC = ∠BCA = ∠ABC = 60°

(ii) We know that, the angle subtended by an arc at the centre of a circle is twice the angle subtended by it at any point on the remaining part of the circle.
∴ ∠BOC = 2∠BAC = 2 × 60° = 120°
Hence, ∠BOC = 120°.

(iii) Yes, employment provided to handicapped persons is important for the development of a society. It helps them to live with dignity in the society.

Question 3.
In the given figure, if:
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\), then calculate the values of x, y and z.

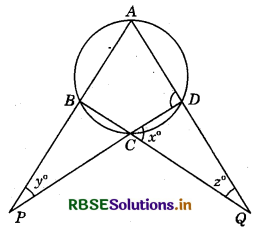
Answer:
Let \(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\) = k (say)
Since,
In ΔDCQ,
∠CDQ = 180° - (3k + 5k)
= 180° - 8k 'P Q'
∠ADC + ∠CBA = 180° (∵ Opposite angles of cyclic quadrilateral ABCD are supplementary.)
8k + ∠CBA = 180° [∵ ∠ADC = x + z (Exterior angle of ΔCDQ)
= (3k + 5k) = 8k
∴ ∠CBA = 180 - 8k
∠PBC = 1800 - ∠ABC
= 180° - (180° - 8k) = 8k

In ΔPBC, ∠P + ∠B + ∠C = 180° ⇒ y + 8k + x = 180°
4k + 8k + 3k = 180°
⇒ 15k = 180°
⇒ k = \(\frac{180^{\circ}}{15}\) = 12°
∴ 3k = 3 × 12 = 36°
= 4k = 4 × 12 = 48°
= 5k = 5 × 12 = 60°

Question 4.
Two circles whose centres are O and O' intersect at P. Through P, a line l parallel to OO' intersecting the circles at C and D is drawn. Prove that CD = 200.

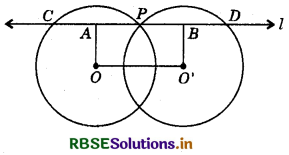
Answer:
Draw OA ⊥ and OB ⊥ l
Now, OA ⊥ l ⇒ OA ⊥ CP
⇒ CA = AP (∵ Perpendicular from the centre bisects the chord)
⇒ CP = 2AP ..........(1)
and O'B ⊥ l ⇒ O'B ⊥ PD
⇒ BP = BD
⇒ PD = 2PB ...........(2)
∴ CD = CP + PD
⇒ CD = 2AP + 2PB [Using equations (1) and (2)]
⇒ CD = 2(AP + PB)
⇒ CD =2AB
= 2OO' (∵ ABO'O is a rectangle.)
Hence proved.

Question 5.
AB and AC are two chords of a circle of radius r such that AB = 2AC. If p and q are the distances of AB and AC from the centre, then prove that: 4q² = p² + 3r².
Answer:
Let AC = a, then AB = 2a.

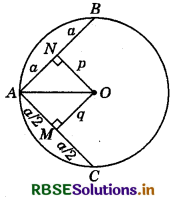
From centre O, perpendicular is drawn to the chords AC and AB at M and N respectively.
∴ AM = MC = \(\frac{a}{2}\) and AN = NB = a
In ΔOMA and ΔONA,
(AO)² = (AM)² + (MO)²
(By Pythagoras theorem)
⇒ (AO)² = \(\left(\frac{a}{2}\right)^{2}\) + (q)²
and AO² = (AN)² + (NO)²
⇒ (AO)² = (a)² + (p)²

From equations (1) and (2), we get:
\(\left(\frac{a}{2}\right)^{2}\) + (q)² = a² + p²
= \(\frac{a^{2}}{4}\) + q² = a² + p²
⇒ a² + 4q² = 4a² + 4p²
⇒ 4q² = p² + 3(a² + p²)
⇒ 4q² = p² + 3r² (∵ In right-angled ΔONA, r² = a² + p²)
Hence Proved.