RBSE Class 9 Maths Important Questions Chapter 1 Number Systems

Rajasthan Board RBSE Class 9 Maths Important Questions Chapter 1 Number Systems Important Questions and Answers.

RBSE Class 9 Maths Chapter 1 Important Questions Number Systems

I. Multiple Choice Questions :
Choose the correct answer from the given options.

Question 1.
Which of the following is an irrational number?
(a) \(\sqrt{\frac{4}{9}}\)
(b) \(\frac{\sqrt{12}}{\sqrt{3}}\)
(c) √7
(d) √81
Answer:
(c) √7

Question 2.
A rational number lying between √2 and √3 is :
(a) \(\frac{\sqrt{2}+\sqrt{3}}{2}\)
(b) √6
(c) 1.6
(d) 1.9
Answer:
(c) 1.6

Question 3.
An irrational number lying between 2 and 3 is :
(a) √5
(b) √13
(c) 2.41
(d) √2
Answer:
(a) √5

Question 4.
√10 × √l5 is equal to :
(a) 6√5
(b) 5√6
(c) √25
(d) 10√5
Answer:
(b) 5√6

Question 5.
The product \(\sqrt[3]{2} \cdot \sqrt[4]{2} \cdot \sqrt[12]{32}\) is equal to :
(a) √2
(b) 2
(c) \(\sqrt[12]{2}\)
(d) \(12 \sqrt{32}\)
Answer:
(b) 2

Question 6.
Decimal representation of a rational number cannot be :
(a) terminating
(b) non-terminating
(c) non-terminating
(d) non-terminating non-repeating
Answer:
(d) non-terminating non-repeating

Question 7.
\(\sqrt[4]{\sqrt[3]{2^{2}}}\) is equal to :
(a) 2^-1/6
(b) 2^-6
(c) 2^1/6
(d) 2⁶
Answer:
(c) 2^1/6

Question 8.
If √2 = 1.4142, then \(\sqrt{\frac{\sqrt{2}-1}{\sqrt{2}+1}}\) equal to :
(a) 2.4142
(b) 5.8284
(c) 0.4142
(d) 0.1718
Answer:
(c) 0.4142

Question 9.
\(\frac{1}{\sqrt{9}-\sqrt{8}}\)
(a) \(\frac{1}{2}\)(3 - 2√2)
(b) \(\frac{1}{3+2 \sqrt{2}}\)
(c) 3 - 2√2
(d) 3 + 2√2
Answer:
(d) 3 + 2√2

Question 10.
2√3 + √3 is equal to :
(a) 2√6
(b) 6
(c) 3√3
(d) 4√6
Answer:
(c) 3√3

Question 11.
The value of 1.999 in the form of \(\frac{p}{q}\), where p and q are integers and q ≠ 0, is:
(a) \(\frac{19}{20}\)
(b) \(\frac{1999}{1000}\)
(c) 2
(d) \(\frac{1}{9}\)
Answer:
(c) 2

Question 12.
π is:
(a) a rational number
(b) an integer
(c) an irrational number
(d) a whole number
Answer:
(c) an irrational number

Question 13.
If \(x^{\frac{1}{12}}\) = \(49^{\frac{1}{24}}\), then x is equal to :
(a) 49
(b) 2
(c) 12
(d) 7
Answer:
(d) 7

Question 14.
Which of the following is not equal to \(\left[\left(\frac{5}{6}\right)^{1 / 5}\right]^{-1 / 6}\)
(a) 

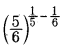
(b) \(\frac{1}{\left[\left(\frac{5}{6}\right)^{1 / 5}\right]^{1 / 6}}\)
(c) \(\left(\frac{6}{5}\right)^{1 / 30}\)
(d) \(\left(\frac{5}{6}\right)^{-1 / 30}\)
Answer:
(a) 

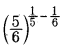
Question 15.
Which of the following is equal to x?
(a) \(x^{\frac{12}{7}}-x^{\frac{5}{7}}\)
(b) \(\sqrt[12]{\left(x^{4}\right)^{1 / 3}}\)
(c) \(\left(\sqrt{x^{3}}\right)^{2 / 3}\)
(d) \(x^{\frac{12}{7}} \times x^{\frac{7}{12}}\)
Answer:
 (c) \(\left(\sqrt{x^{3}}\right)^{2 / 3}\)

II. Fill in the blanks

Question 1.
Rational number between \(\frac{1}{9}\) and \(\frac{2}{9}\) is _______________ .
Answer:
\(\frac{1}{6}\)

Question 2.
\(\frac{p}{q}\) form of 0.6 + 0.\(\overline{7}\) + 0.4\(\overline{7}\) is _______________ .
Answer:
\(\frac{167}{90}\)

Question 3.
The rationalizing factor of the denominator in \(\frac{1}{\sqrt{2}+\sqrt{3}}\) is _______________ .
Answer:
√2 - √3

Question 4.
If \(\frac{\sqrt{3}-1}{\sqrt{3}+1}\) = a + b√3, then a = _____________ and b = _______________ . 
Answer:
2, - 1

Question 5.
If a = 2 and 6 = 3, then the value of (a^a + b^b)^-1 = _______________ .
Answer:
\(\frac{1}{31}\)

III. True/False:

State whether the following statements are True or False.
Question 1.
The decimal expansion of a rational number is non-terminating non-recurring.
Answer:
False

Question 2.
1 is the smallest prime number.
Answer:
False

Question 3. 
\(\frac{\sqrt{18}}{\sqrt{2}}\) is a rational number.
Answer:
True

Question 4.
2.0200200200002..... is an irrational number.
Answer:
True

Question 5.
Between two rational numbers there is exactly one rational number.
Answer:
False

Question 6.
The product of any two irrational numbers is always an irrational number.
Answer:
False

Question 7.
There are infinitely many integers between any two integers.
Answer:
False

IV. Match the Columns:

Match the column I with the column II.

Column I	Column II
(1) 6.\(\overline{54}\) is ……….	(i) 14
(2) π is ……….	(ii) 6
(3) The length of period of \(\frac{1}{7}\) is ………	(iii) a rational  number
(4) If x = (2 - √3), then \(\left(x^{2}+\frac{1}{x^{2}}\right)\)........... .	(iv) an irrational number

Answer:

Column I	Column II
(1) 6.\(\overline{54}\) is ……….	(iii) a rational number
(2) π is ……….	(iv) an rational number
(3) The length of period of \(\frac{1}{7}\) is ………	(ii) 6
(4) If x = (2 - √3), then \(\left(x^{2}+\frac{1}{x^{2}}\right)\)........... .	(i) 14

V. Very Short Answer Type Questions:

Question 1.
Find the value of (256)^0.16 × (256)^0.09.
Answer:
(256)^0.16 × (256)^0.09 = (256)^{0.16 + 0 09}  (∵ a^m × aⁿ = a^m+n)
= (256)^0.25
= \((256)^{\frac{25}{100}}=(256)^{\frac{1}{4}}=\left(4^{4}\right)^{\frac{1}{4}}=4\)

Question 2.
If a = 2, b = 3 then find the values of (a^a + b^b)^-1.
Answer:
(a^a + b^b)-1 = (2² + 3³)^-1 = (4 + 27)^-1 = (31)^-1 = \(\frac{1}{31}\)

Question 3.
Simplify: (7)^_-3 (9)^-3
Answer:
(7)^-3 (9)^-3 = (7 × 9)^-3
= (63)^-3 = \(\frac{1}{(63)^{3}}\)

Question 4. 
Taking  √2 = 1.414 and π = 3.141, evaluate \(\frac{1}{\sqrt{2}}\) + π upto three places of decimal. 
Answer:

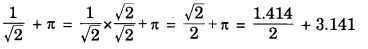
= 0.707 + 3.141 = 3.848

Question 5.
\(\frac{\sqrt{147}}{\sqrt{75}}\) is not a rational number as √l47 and √75 are not rational. State wheather it is true or false. Justify your answer.
Answer:
\(\frac{\sqrt{147}}{\sqrt{75}}=\frac{\sqrt{3 \times 7 \times 7}}{\sqrt{3 \times 5 \times 5}}=\frac{7 \sqrt{3}}{5 \sqrt{3}}=\frac{7}{5}\)
Which is clearly a rational number.
Hence, the given statement is false.

VI. Short Answer Type Questions:

Question 1.
Express 0.00323232..... in the form of  \(\frac{p}{q}\).
Answer:
Let x = 0.00323232...
On multiplying equation (1) by 100, we get:
100x = 0.323232.....
Again, multiplying equation (2) by 100, we get:
10000a: = 32.3232....
On subtracting equation (2) from equation (3), we get:
10000x - 100x = 32.3232..... - 0.3232.....
⇒ 9900x = 32
⇒ x = \(\frac{32}{9900}=\frac{8}{2475}\)
Hence, 0.003232..... = \(\frac{8}{2475}\)

Question 2.
If 125^x = \(\frac{25}{\mathbf{5}^{x}}\), then find the value of x. 
Answer:
Given,  25^x = \(\frac{25}{\mathbf{5}^{x}}\)
⇒ 5^3x = 5^{2 - x}
On equating power from both sides, we get:
3x = 2 - x
⇒ 4x = 2
∴ x =  \(\frac{2}{4}=\frac{1}{2}\)

Question 3.
If a = 7 - 4√3, then find the value of √a + \(\frac{1}{\sqrt{a}}\)
Answer:

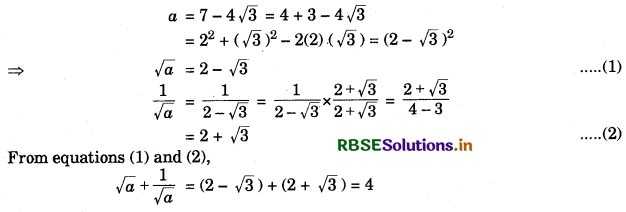
Question 4.    
How many irrational numbers lie between √2 and √3? Find any three irrational numbers lying between √2 and √3.
Answer:
Infinitely many irrational numbers lie between √2 and √3.
One irrational number between √2 and √3 is \(\sqrt{\sqrt{2} \sqrt{3}}\) = \(\sqrt{\sqrt{6}}\) = \(6^{\frac{1}{4}}\)
Another irrational number between √2 and √3 is \(\sqrt{\sqrt{2} 6^{\frac{1}{4}}}\)
= \(2^{\frac{1}{4}} \cdot 6^{\frac{1}{8}}=2^{\frac{1}{4}} \cdot 2^{\frac{1}{8}} \cdot 3^{\frac{1}{8}}=2^{\frac{1}{4}+\frac{1}{8}} \cdot 3^{\frac{1}{8}}=2^{\frac{3}{8}} \cdot 3^{\frac{1}{8}}\)
Third irrational number between √2 and √3 is
\(\sqrt{\sqrt{2} 2^{\frac{3}{8}} \cdot 3^{\frac{1}{8}}}\) = \(2^{\frac{1}{4}} \cdot 2^{\frac{3}{16}} \cdot 3^{\frac{1}{16}}\)= \(2^{\frac{7}{16}} \cdot 3^{\frac{1}{16}}\)

Question 5.
Show that 

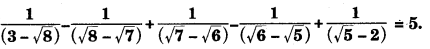
Answer:


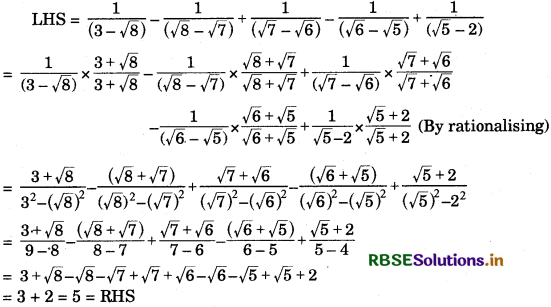
Question 6.
If 2^x = 3^y = 6^z, then prove that \(\frac{1}{x}+\frac{1}{y}-\frac{1}{z}\)= 0 or z = \(\frac{x y}{x+y}\)
Answer:
Let 2^x = 3^y = 6^z = k
⇒ 2^x = k,3^y = k and 6^Z = k
⇒ 2 = \(k^{1 / x}\), 3 = \(k^{1 / y}\) and 6 = \(k^{1 / z}\)
Now, 6 = \((k)^{1 / z}\)
⇒ 2 × 3 = \((k)^{1 / z}\)
⇒ \((k)^{1 / x} \times(k)^{1 / y}=(k)^{1 / z}\)
⇒ \((k)^{1 / x+1 / y}=(k)^{1 / z}\)
On equating the power from both sides, we get:

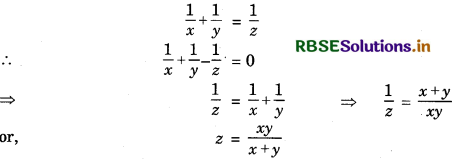
Question 7.

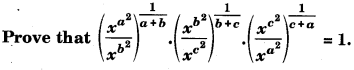
Answer:

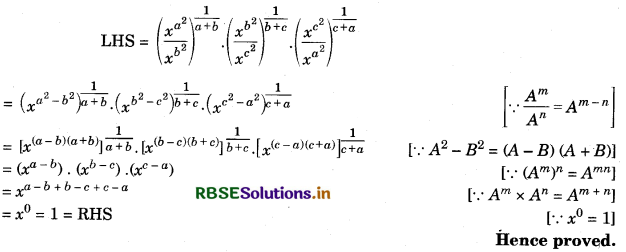
VII. Long Answer Type Questions:

Question 1. 
Write the following in decimal form and say, what kind of decimal expansion each has?
(i) \(\frac{36}{100}\)
Answer:
\(\frac{36}{100}\) = 0.36, so it has terminating decimal expansion

(ii) 5\(\frac{1}{8}\)
Answer:
5\(\frac{1}{8}\) = \(\frac{41}{8}\) = 5.125, so it has terminating decimal expansion.

(iii) \(\frac{4}{13}\)
Answer:
\(\frac{4}{13}\) = 0 . \(\overline{307692}\), so it has non-terminating repeating decimal expansion. 

(iv) \(\frac{2}{15}\)
Answer:
\(\frac{2}{15}\) = 0.1\(\overline{3}\), so it has non-terminating repeating decimal expansion. 

(v) \(\frac{329}{500}\)
Answer:
\(\frac{329}{500}\) = 0.658, so it has terminating decimal expansion.

Question 2. 
Express \(1.\overline{32}\) + \(0.\overline{35}\) in the form \(\frac{p}{q}\) where p and q are integers and q ≠ 0.
Answer: 
Let x = \(1.\overline{32}\)
Then  x  =  1.3232...
⇒ 10x  =  13.232... ........... (1)        
⇒ 100x = 132.323... ........... (2)    
Subtracting equations (1) from (2), we get:
90x = 119    
⇒ x = \(\frac{119}{90}\) ............... (3)
Let x = \(0.\overline{35}\)
Then x = 0.35 35 35 ... ............... (4)
⇒ 100x = 35.35 35 35 ... ............... (5)
Subtracting equations (4) from (5), we get
99x  = 35    

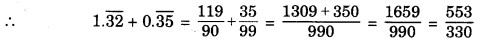
⇒ x = \(\frac{35}{99}\)
Here, p = 553, q = 330(≠ 0)

Question 3. 
Simplify the following into a fraction with rational denominator \(\frac{1}{\sqrt{5}+\sqrt{6}-\sqrt{11}}\)
Answer: