RBSE Class 10 Maths Important Questions Chapter 8 त्रिकोणमिति का परिचय

Rajasthan Board RBSE Class 10 Maths Important Questions Chapter 8 त्रिकोणमिति का परिचय Important Questions and Answers.

RBSE Class 10 Maths Chapter 8 Important Questions त्रिकोणमिति का परिचय

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
\(\frac{\tan \theta}{\sqrt{1+\tan ^{2} \theta}}\) के बराबर है
(A) cos θ
(B) sin θ
(C) sec θ
(D) cot θ
उत्तरः
(B) sin θ

प्रश्न 2.
\(\sqrt{{cosec}^{2} \theta-1}\) बराबर है
(A) cos θ
(B) sec θ
(C) sin θ
(D) cosec θ
उत्तरः
(A) cos θ

प्रश्न 3.
sin θ cosec θ + cos θ sec θ बराबर है
(A) 2
(B) 1
(C) \(\frac{1}{2}\)
(D) - 1
उत्तरः
(A) 2

प्रश्न 4.
2 cosec 30° sec 30° बराबर है-
(A) \(\frac{2}{\sqrt{3}}\)
(B) \(\frac{\sqrt{3}}{2}\)
(C) 8
(D) \(\frac{8}{\sqrt{3}}\)
उत्तरः
(D) \(\frac{8}{\sqrt{3}}\)

प्रश्न 5.
यदि sin θ = \(\frac{\sqrt{3}}{2}\) है, तो θ का मान है
(A) 30°
(B) 45°
(C) 60°
(D) 90°
उत्तरः
(C) 60°

प्रश्न 6.
\(\frac{3 \sec 51^{\circ}}{{cosec} 39^{\circ}}\) का मान है
(A) 1
(B) 2
(C) 3
(D) 0
उत्तरः
(C) 3

प्रश्न 7.
यदि cos (90° - θ) = \(\frac{1}{2}\) हो तो 0 का मान होगा
(A) 90°
(B) 60°
(C) 450
(D) 30°
उत्तरः
(D) 30°

प्रश्न 8.
sin² 50° + cos² 50° +. 1 बराबर है-
(A) 2
(B) 1
(C) \(\frac{1}{2}\)
(D) 0
उत्तरः
(A) 2

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
यदि sin 3A = cos (A - 26°) हो, जहाँ 3A एक न्यून कोण है तो A का मान ज्ञात कीजिये।
हल:
दिया गया है-
sin 3A = cos (A - 26°)
sin 3A = cos (90° - 3A)
∵ cos (90° - 3A) = cos (A - 26°)
क्योंकि 90° - 3A और A - 26° दोनों ही न्यूनतम कोण हैं,
∴ 90° - 3A = A - 26°
या 4A = 90° + 26° = 116°
A = \(\frac{116^{\circ}}{4}\) = 29°

प्रश्न 2.
cot 85° + cos 75° को 0° और 45° के बीच के कोणों के त्रिकोणमितीय अनुपातों के पदों में व्यक्त कीजिये।
हल:
cot 85° . cos 75°
= cot (90° - 5°) + cos (90° - 15°)
= tan 5° + sin 15°

प्रश्न 3.
sin 25° cos 65° + cos 25° sin 65° + sin² 25° + sin² 65° का मान ज्ञात कीजिये।
हल:
sin 25° cos 65° + cos 25° . sin 65° + sin² 25° + sin² 65°
= sin (90° - 65°) . cos 65° + cos(90° - 65°) . sin 65° + sin² (90° - 65°) + sin² 65°
= cos 65° . cos 65° + sin 65° sin 65° + cos² 65° + sin² 65°
= cos² 65° + sin² 65° + cos² 65° + sin² 65°
= 1 + 1 = 2

प्रश्न 4.
यदि ∠A < 90° एवं ∠B < 90° और sin A = cos B हो तो सिद्ध किजिये A + B = 90°
हल:
⇒ sin A = cos B
⇒ sin A = sin (90° - B)
⇒ A = 90° - B
⇒ A + B = 90° (इतिसिद्धम्)

प्रश्न 5.
यदि sin θ = cos θ तो θ का मान ज्ञात कीजिये।
हल:
⇒ sin θ = cos θ
⇒ sin θ = sin (90° - θ)
⇒ θ = 90° - θ
⇒ 2θ = 90°
⇒ θ = \(\frac{90^{\circ}}{2}\) = 45° उत्तर

प्रश्न 6.
4 sin 18° sec 72° का मान लिखिए।
हल:
4 sin 18° sec 72° = 4 sin 18° sec (90° - 18°)
= 4 sin 18° . cosec 18°
= 4 sin 18° × \(\frac{1}{\sin 18^{\circ}}\) = 4

प्रश्न 7.
sin θ cos (90° - θ) + cos θ sin (90° - θ) + 1 का मान लिखिए।
हल:
sin θ sin θ + cos θ cos θ + 1
= sin²θ + cos²θ + 1
= 1 + 1 = 2

प्रश्न 8.
sin² 60° + cos² 30° का मान लिखिए।
हल:
\(\left(\frac{\sqrt{3}}{2}\right)^{2}+\left(\frac{\sqrt{3}}{2}\right)^{2}\) = \(\frac{3}{4}+\frac{3}{4}\)
= \(\frac{6}{4}\) = \(\frac{3}{2}\)

प्रश्न 9.
cos² 50° + cos² 40° का मान ज्ञात कीजिए।
हल:
cos² 50° + cos² (90° - 50°) ।
= cos² 50° + sin² 50°
= 1

प्रश्न 10
\(\frac{\sqrt{1-\sin ^{2} 40^{\circ}}}{\cos 40^{\circ}}\) का सरलतम मान लिखिए।
हल:
\(\frac{\sqrt{\cos ^{2} 40^{\circ}}}{\cos 40^{\circ}}\) = \(\frac{\cos 40^{\circ}}{\cos 40^{\circ}}\) = 1

प्रश्न 11.
3 sin 60° - 4 sin³ 60° का मान ज्ञात कीजिए।
हल:
3 sin 60° - 4 sin³ 60°

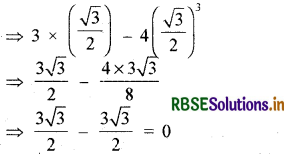
प्रश्न 12.
sin θ . cosec θ - cos θ sec θ का मान ज्ञात कीजिए।
हल:
sin θ . cosec θ - cos θ . sec θ
= sin θ . \(\frac{1}{\sin \theta}\) - cos θ . \(\frac{1}{\cos \theta}\) = 1 - 1
= 0

प्रश्न 13.
(1 - sin² θ) sec² θ का मान लिखिए।
हल:
(1 - sin² θ) sec² θ
= cos² θ . sec² θ
= cos² θ . \(\frac{1}{\cos ^{2} \theta}\) = 1

प्रश्न 14.
\(\frac{1}{\sqrt{{cosec}^{2} \theta-1}}\) का मान लिखिए।
हल:

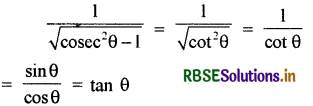
प्रश्न 15
\(\frac{\cos \theta}{\sin \theta}\) × cot θ × tan θ का मान लिखिए।
हल:

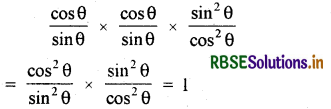
प्रश्न 16.
2 sin² A (1 + cot² A) का मान लिखिए।
हल:
2 sin² A × cosec² A
= 2 sin² A × \(\frac{1}{\sin ^{2} A}\) = 2

प्रश्न 17.
त्रिकोणमितीय अनुपात tan A को sec A के पदों में लिखिए।
हल:
1 + tan² A = sec² A
tan² A = sec² A - 1
(tan A)² = sec² A - 1
∴ tan A = ± \(\sqrt{\sec ^{2} A-1}\)
[न्यून कोण A के लिए -ve चिह्न को छोड़ने पर]
अर्थात् tan A = \(\sqrt{\sec ^{2} A-1}\)

लघूत्तरात्मक प्रश्न

प्रश्न 1.
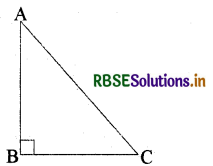
एक समकोण त्रिभुज ABC में, जिसका कोण B समकोण है, यदि tan A = 1 तो सत्यापित किजिए 2 sin A cos A = 1
हल:
∆ ABC में
tan A = \(\frac{\mathrm{BC}}{\mathrm{AB}}\) = 1
अर्थात् BC = AB
माना AB = BC = K
जहाँ पर K एक धन संख्या है।
पाइथागोरस प्रमेय से

(AC)² = (AB)² + (BC)²
= (K)² + K².
(AC)² = 2K²
∴ AC = K√2
अतः sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{\mathrm{K}}{\mathrm{K} \sqrt{2}}\) = \(\frac{1}{\sqrt{2}}\)
और cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}\) = \(\frac{\mathrm{K}}{\mathrm{K} \sqrt{2}}\) = \(\frac{1}{\sqrt{2}}\)
∴ 2 sin A cos A = \(2\left(\frac{1}{\sqrt{2}}\right)\left(\frac{1}{\sqrt{2}}\right)\) = \(\frac{2}{2}\) = 1.
जो कि अपेक्षित मान है।

प्रश्न 2.
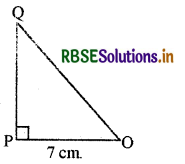
∆OPO में, जिसका कोण P समकोण है, OP = 7 cm. और 00 - PQ = 1 cm. ( देखिये आकृति), sin Q और cos Q के मान ज्ञात कीजिये।
हल:
चित्र की आकृति से OQ² = OP² + PQ²

लेकिन दिया है
OQ - PO = 1
∴ OQ = 1 + PQ
अर्थात् (1 + OQ)² = OP² + PQ²
अर्थात् 1 + PQ² + 2PQ = OP² + PO²
अर्थात् 1 + 2PQ = (7)²
1 + 2PQ = 49
∴ PQ = 24 cm
और OQ = 1 + PQ = 1 + 24 = 25 cm
sin Q = \(\frac{O P}{O Q}\) = \(\frac{7}{25}\)
और cos Q = \(\frac{P Q}{O Q}\) = \(\frac{24}{25}\)

प्रश्न 3.
यदि tan A = \(\frac{3}{4}\) हो, तो sec A (1 - sin A) (sec A + tan A) का मान ज्ञात कीजिये।
हल:
माना कि ABC एक समकोण त्रिभुज है, जिसमें कोण B समकोण है।
∠A के लिये

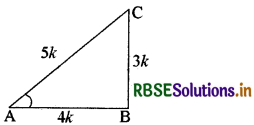
आधार = AB, लम्ब = BC तथा कर्ण = AC दिया गया है, tan A = \(\frac{3}{4}\)

प्रश्न 4.
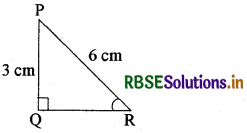
∆PQR में, जिसका कोण Q समकोण है। दी गयी आकृति में, PQ = 3cm और PR = 6 cm है। ∠QPR और ∠PRQ ज्ञात कीजिये।

हल:
दिया हुआ है
PQ = 3 cm और PR = 6cm
इसलिये
\(\frac{P Q}{P R}\) = sin R
sin R = \(\frac{3}{6}\) = \(\frac{1}{2}\) = sin 30°
अतः ∠PRQ = 30°
और इसलिये ∠QPR = 180° - (90° + 30°) = 60°

प्रश्न 5.
6 tan 20° tan 70° – 3 sec² 45° का मान ज्ञात कीजिए।
हल:
6 tan 20° tan 70° - 3 sec² 45°
= 6 tan 20° . tan (90° - 20°)- 3 sec² 45°
= 6 tan 20° . cot 20° - 3 (√2)²
∵ tan θ × cot θ = 1
= 6 - 6 = 0

प्रश्न 6.
sin 30° . cos2 30° + tan 45° . cost 60° का मान ज्ञात कीजिए।
हल:
sin 30° . cos2 30° + tan 45° . cos 60°

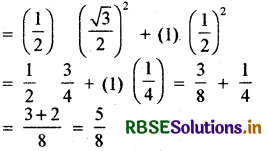
प्रश्न 7.
यदि sin (A - B) = \(\frac{1}{2}\) तथा cos (A + B) = 7, 0° < A + B ≤ 90°, A > B, तो A और B ज्ञात कीजिये।
हल:
क्योंकि
sin (A - B) = \(\frac{1}{2}\)
∴ sin (A - B) = sin 30°
⇒ A - B = 30°
इसी तरह सेcos (A + B) = \(\frac{1}{2}\)
∴ cos (A + B) = cos 60°
⇒ A + B = 60° ..... (ii)
समीकरण (i) तथा (ii) को जोड़ने पर
A - B + A + B = 30° + 60° = 90°
2A = 90°
A = 45°
समीकरण (ii) से B = 15°

प्रश्न 8.
(sec² 30° + cosec² 45°) (2 cos 60° + sin 90° + tan 45°) का मान ज्ञात कीजिए।
हल:
(sec² 30° + cosec² 45°) (2 cos 60° + sin 90° + tan 45°)

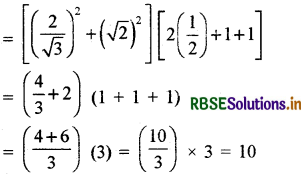
प्रश्न 9.
sec² 65° - cot² 25° - 2 sin 30° cos 60° का मान ज्ञात कीजिए।
हल:
sec² 65° - cot² 25° - 2 sin 30° cos 60°
यहाँ 25° = 90° - 65° करने पर
cot (25°) = cot (90° - 65°)
cot 25° = tan 65°
[∵ cot (90° - θ) = tan θ]
अब व्यंजक इस प्रकार हो जाएगा
(sec² 65° - tan² 65°) - 2 sin 30° cos 60°
= 1 - 2 × \(\frac{1}{2}\) × \(\frac{1}{2}\)
[∵ sec² θ - tan² θ = 1]
= 1 - \(\frac{1}{2}\)
= \(\frac{1}{2}\)

प्रश्न 10.
\(5\frac{\sin 17^{\circ}}{\cos 73^{\circ}}+2 \frac{\cos 67^{\circ}}{\sin 23^{\circ}}-6 \frac{\sin 15^{\circ}}{\cos 75^{\circ}}\) का मान ज्ञात कीजिए।
हल:
sin 17° = sin (90° - 73°)
या sin 17° = cos 73° .... (i)
cos 67° = cos (90° - 23°)
या cos 67° = sin 23° .... (ii)
sin 15° = sin (90° - 75°)
या sin 15° = cos 75° ..... (iii)
समीकरण (i), (ii) व (iii) से sin 17°, cos 67° व sin 15° के मान मूल व्यंजक में रखने पर
= \(5 \frac{\cos 73^{\circ}}{\cos 73^{\circ}}+2 \frac{\sin 23^{\circ}}{\sin 23^{\circ}}-6 \frac{\cos 75^{\circ}}{\cos 75^{\circ}}\)
= 5 (1) + 2 (1) - 6 (1)
= 5 + 2 - 6
= 7 - 6
= 1

प्रश्न 11.
सिद्ध कीजिये कि sec A (1 - sin A) (sec A + tan A) = 1
हल:
L.H.S.= sec A (1 - sin A) (sec A + tan A)

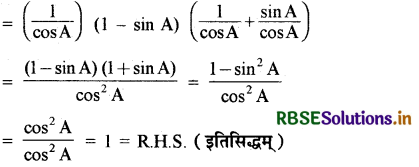
प्रश्न 12.
यदि sin θ = \(\frac{1}{2}\), तो (tan θ + cot θ)² का मान लिखिए।
हल:

प्रश्न 13.
यदि sin A = \(\frac{3}{5}\) हो, तो cos A और cosec A ज्ञात कीजिए।
हल:
माना कि ABC कोई समकोण त्रिभुज है जिसमें कोण B पर समकोण है। ∵ sin A = \(\frac{3}{5}\)

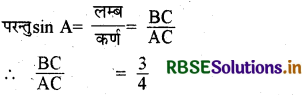
माना BC = 3k
AC = 5k

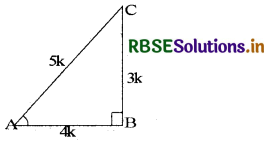
पाइथागोरस प्रमेय से
AC² = AB² + BC²
या (5k²) = (AB)² + (3k)²
या 25k² = AB² + 9k²
या 25k² - 9k² = AB²
या 16k² = AB²
या AB = 4k

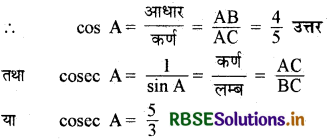
प्रश्न 14.
\(\frac{\tan 65^{\circ}}{\cot 25^{\circ}}\) का मान ज्ञात कीजिए।
हल:
tan 65°
हम जानते हैं कि cot A = tan (90° - A)
अतः cot 25° = tan (90° - 25°)
= tan 65°
अर्थात् \(\frac{\tan 65^{\circ}}{\cot 25^{\circ}}\) = \(\frac{\tan 65^{\circ}}{\tan 65^{\circ}}\)
= 1

प्रश्न 15.
sin 35° cos 55° + cot 35° sin 55° का मान ज्ञात कीजिए।
हल:
sin 35° cos 55° + cot 35° sin 55°
= sin 35° × cos (90° - 35°) + cos 35° × sin (90° - 35°)
[∵ cos (90°- θ) = sin θ]
[ sin (90°- θ) = cos θ]
= sin 35° × sin 35° + cos 35° x× cos 35°
= sin² 35° + cos² 35° = 1

प्रश्न 16.
यदि sin θ = \(\frac{1}{2}\) हो, तो \(\frac{1-2 \sin ^{2} \theta}{\sin \theta}\) का मान ज्ञात कीजिए।
हल:
दिया गया व्यंजक = \(\frac{1-2 \sin ^{2} \theta}{\sin \theta}\)
यहाँ sin θ = \(\frac{1}{2}\) रखने पर

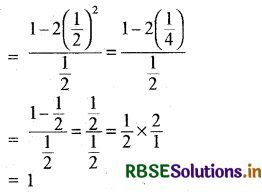
प्रश्न 17.
cos² 12° + cos² 78° का मान ज्ञात कीजिए।
हल:
cos² 12° + cos² 78°
= cos² 12° + {cos (90° - 12°)}²
= cos² 12° + sin² 12° [∵ cos (90° - θ) = sin θ]
= 1

प्रश्न 18.
दिखाइए कि tan 36° tan 17° tan 54° tan 730 = 1
हल:
tan 36° tan 17° tan 54° tan 73°
= tan 36° tan 17° tan (90° - 36°) tan (90° - 17°)
= tan 36° . tan 17° cot 36° cot 17°
= tan 36° . cot 36° . tan 17° . cot 17°
= 1.1 = 1

प्रश्न 19.
दिखाइए कि sin 28° cos 62° + cos 28° sin 62° = 1.
हल:
sin 28° cos 62° + cos 28° sin 62°
= sin 28° × cos (90° - 28°) + cos 28° × sin (90° - 28°)
[∵ cos (90° - θ) = sin θ तथा sin (90° - θ) = cos θ]
= sin 28° . sin 28° + cos 28° . cos 28°
= sin² 28° + cos² 28°
= 1

प्रश्न 20.
\(\frac{\tan 67^{\circ}}{\cot 23^{\circ}}\) का मान ज्ञात कीजिए।
हल:
\(\frac{\tan 67^{\circ}}{\cot 23^{\circ}}\)
हम जानते हैं कि cot A = tan (90° - A)
अतः cot 23° = tan (90° - 23°) = tan 67°
अर्थात् \(\frac{\tan 67^{\circ}}{\cot 23^{\circ}}\) = \(\frac{\tan 67^{\circ}}{\tan 67^{\circ}}\) = 1

प्रश्न 21.
यदि 3 cot A = 4, तो \(\frac{1-\tan ^{2} A}{1+\tan ^{2} A}\) का मान ज्ञात कीजिए।
हल:
∵ 3 cot A = 4 ∴ cot A = \(\frac{4}{3}\) हम जानते हैं कि

प्रश्न 22.
सिद्ध कीजिए कि \(\left[\frac{1-\tan A}{1-\cot A}\right]^{2}\) = tan² A .
हल:

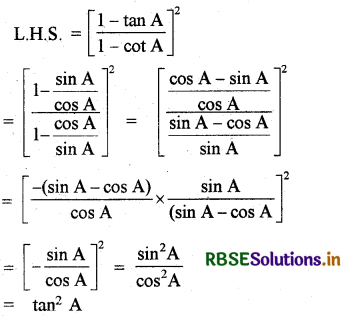
= R.H.S.
∴ L.H.S. = R.H.S. (इतिसिद्धम्)

प्रश्न 23.
यदि cos A = तो cot A का मान परिकलित कीजिए।
हल:
माना कि ABC कोई समकोण त्रिभुज है जिसमें कोण B पर समकोण है।
cos A = \(\frac{12}{13}\)

माना AB = 12k
AC = 13k
पाइथागोरस प्रमेय से
AC² = AB² + BC²
∴ BC² = AC² - AB²
= (13k)² - (12k)²
= 169k² - 144k² = 25k²
∴ BC = 5k

निबन्धात्मक प्रश्न

प्रश्न 1.
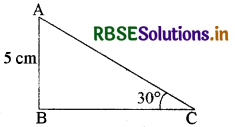
∆ABC में जिसका कोण B समकोण है, AB = 5 cm और ∠ACB = 30° ( देखिए आकृति)। भुजाओं BC और AC की लम्बाइयाँ ज्ञात करें।
हल:
भुजा BC की लम्बाई ज्ञात करने के लिए हम उस त्रिकोणमितीय अनुपात को लेंगे जिसमें BC और दी हुई भुजा AB हो। क्योंकि BC कोण C की संलग्न भुजा है, और AB कोण C की सम्मुख भुजा है, इसलिए
\(\frac{\mathrm{AB}}{\mathrm{BC}}\) = tan c
अर्थात् \(\frac{5}{\mathrm{BC}} \) = tan 30° = \(\frac{1}{\sqrt{3}}\)
जिससे BC = 5√3 cm
नुजा AC का लम्बाई ज्ञात करने के लिए
∵ sin 30° = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
अर्थात् \(\frac{1}{2}\) = \(\frac{5}{A C}\)
अर्थात् AC = 10 cm

प्रश्न 2.
यदि ∠B और ∠Q ऐसे न्यूनकोण हों जिससे sin B = sin Q, at ftese allery for ZB = 20.
हल:
हम दो समकोण त्रिभुज ABC और PQR लें, जहाँ sin B = sin Q (देखिए आकृति)।


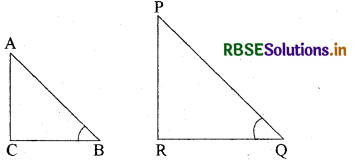
समीकरण (i) और (ii) से
\(\frac{A C}{P R}\) = \(\frac{A B}{P Q}\) = \(\frac{B C}{Q R}\)
तब प्रमेय का प्रयोग करने पर ∆ACB ~ ∆PRQ अतः ∠B = ∠Q (इतिसिद्धम्)

प्रश्न 3.
यदि θ = 30° तो निम्नलिखित का मान ज्ञात कीजिए
\(\frac{3 \cot \left(90^{\circ}-30^{\circ}\right)-\tan ^{3} 30^{\circ}}{1-3 \cot ^{2}\left(90^{\circ}-30^{\circ}\right)}\)
हल:
θ = 30° रखने पर व्यंजक होगा

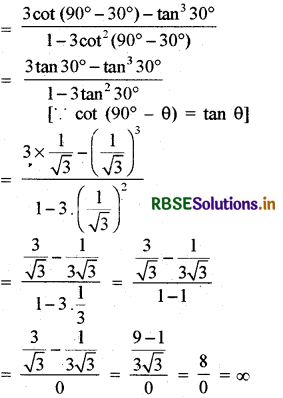
प्रश्न 4.
सिद्ध कीजिए-
tan 6° . tan 26° tan 64° . tan 84° = 1
हल:
L.H.S.= tan 6° . tan 26° tan 64° . tan 84°
∵ 6° = 90° - 84°
∴ tan 6° = tan (90° - 84°)
tan 6° = cot 84°
∵ tan (90° - θ) = cot θ .... (i)
तथा 26° = 90° - 64°
tan 26° = tan (90° - 64°)
tan 26° = cot 64° ...... (ii)
समीकरण (i) व (ii) से दिए गए व्यंजक में मान रखने पर
= tan 6° . tan 26° tan 64° . tan 84°
= cot 84° . tan 84° . cot 64° . tan 64°
= 1 . 1 = 1 = R.H.S.

प्रश्न 5.
निम्नलिखित समीकरण से x का मान ज्ञात कीजिए cosec (90° - θ) + x cos θ cot (90° - θ) = sin (90° - θ)
हल:
cosec (90° - θ) + x cos θ cot (90° - θ) = sin (90° - θ)
⇒ sec θ + x cos θ tan θ = cos θ

प्रश्न 6.
निमन का मान ज्ञात किजिये-
(1 + tan θ + sec θ) (1 + cot θ - cosec θ)
हल:
(1 + tan θ + sec θ) (1 + cot θ - cosec θ)

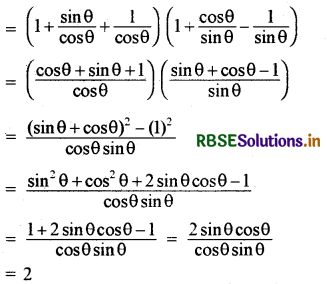
प्रश्न 7.
सिद्ध किजिये
tan² A - tan² B = \(\frac{\cos ^{2} B-\sin ^{2} A}{\cos ^{2} B \cos ^{2} A} = \frac{\sin ^{2} A-\sin ^{2} B}{\cos ^{2} A \cos ^{2} B}\)
हल:
LHS = tan² A - tan² B
= \(\frac{\sin ^{2} A}{\cos ^{2} A}-\frac{\sin ^{2} B}{\cos ^{2} B}\)

प्रश्न 8.
यदि tan θ = \(\frac{1}{\sqrt{7}}\), तो \(\frac{{cosec}^{2} \theta-\sec ^{2} \theta}{{cosec}^{2} \theta+\sec ^{2} \theta}\) का मान लिखिए।
हल:
यहाँ tan θ = \(\frac{1}{\sqrt{7}}\)
हम जानते हैं कि
sec² θ = 1 + tan² θ

प्रश्न 9.
निम्न सर्वसमिका को सिद्ध कीजिये
\(\frac{\sin \mathbf{A}+\cos \mathbf{A}}{\sin \mathbf{A}-\cos \mathbf{A}}+\frac{\sin \mathbf{A}-\cos \mathbf{A}}{\sin \mathbf{A}+\cos \mathbf{A}}\) = \(\frac{2}{\sin ^{2} A-\cos ^{2} A}\)
हल:

प्रश्न 10.
सिद्ध किजिये कि
\(\frac{\cot A-\cos A}{\cot A+\cos A} = \frac{{cosec} A-1}{{cosec} A+1}\)
हल:

= \(\frac{{cosec} A-1}{{cosec} A+1}\) = RHS
∴ LHS = RHS

प्रश्न 11.
सर्वसमिका sec² θ = 1 + tan² θ का प्रयोग करके सिद्ध कीजिए कि
\(\frac{\sin \theta-\cos \theta+1}{\sin \theta+\cos \theta-1}\) = \(\frac{1}{\sec \theta-\tan \theta}\)
हल:
क्योंकि हमें sec θ और tan θ से सम्बन्धित सर्वसमिका प्रयुक्त करनी है, इसलिए सबसे पहले सर्वसमिका के वाम पक्ष के अंश और हर को cos θ से भाग देकर वाम पक्ष को sec θ और tan θ के पदों में रूपान्तरित करने पर

प्रश्न 12.
सिद्ध कीजिए कि
\(\sqrt{\frac{1+\cos A}{1-\cos A}}\) = cosec A + cot A
हल:
L.H.S = \(\sqrt{\frac{1+\cos A}{1-\cos A}}\)
वर्गमूल के अंदर अंश व हर में 1 + cos A का गुणा करने पर
= \(\sqrt{\frac{(1+\cos A)(1+\cos A)}{(1-\cos A)(1+\cos A)}}\)

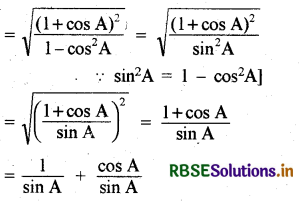
= cosec A + cot A
= R.H.S.
∴ L.H.S. = R.H.S. (इतिसिद्धम्)

प्रश्न 13.
(i) यदि cos 3A = sin(A - 34°) हो, जहाँ 3A एक न्यून कोण है तो A का मान ज्ञात कीजिए।
(ii) निम्नलिखित सर्वसमिका सिद्ध कीजिए, जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित है, न्यून कोण है।
\(\frac{1+\cot ^{2} A}{1+\tan ^{2} A} = \left(\frac{1-\cot A}{1-\tan A}\right)^{2}\)
हल:
(i) यहाँ यह दिया हुआ है कि
cos 3A = sin(A - 34°) ....(1)
क्योंकि cos. 3A = sin(90° - 3A)
इसलिए समीकरण (1) को इस रूप में लिख सकते है।
sin(90° - 3A) = sin(A - 34°)
क्योंकि 90° - 3A और A - 34° दोनों ही न्यून कोण हैं, इसलिए
90° - 3A = A - 34°
या - 3A - A = - 34° - 90°
या - 4A = - 124°
जिससे A = \(\frac{-124}{-4}\) = 31° प्राप्त होता है।
अतः A का मान 31° होगा। उत्तर

हल (ii)