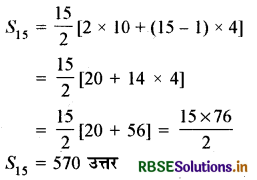RBSE Class 10 Maths Important Questions Chapter 5 समांतर श्रेढ़ियाँ

Rajasthan Board RBSE Class 10 Maths Important Questions Chapter 5 समांतर श्रेढ़ियाँ Important Questions and Answers.

RBSE Class 10 Maths Chapter 5 Important Questions समांतर श्रेढ़ियाँ

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
किसी समान्तर श्रेढ़ी का प्रथम पद 2 तथा सार्व
अन्तर 3 हो, तो समान्तर श्रेढ़ी होगी
(A) 2, 5, 8, 11, .....
(B) 2, 6, 18, 54, .....
(C) 2, 4, - 1, 3, .....
(D) 2, 2, 3, 3, 4, 4, ........
उत्तरः
(A) 2, 5, 8, 11, .....

प्रश्न 2.
16 पदों वाली समान्तर श्रेढ़ी 2, 5, 8, 11, ..... का अन्तिम पद होगा
(A) 47
(B) 48
(C) 49
(D) 46
उत्तरः
(A) 47

प्रश्न 3.
यदि समान्तर श्रेढ़ी का प्रथम पद 5 और पाँचवाँ पद 17 हो, तो पाँच पदों का योग होगा-
(A) 55
(B) 56
(C) 57
(D) 58
उत्तरः
(A) 55

प्रश्न 4.
श्रेढ़ी 72, 70, 68, 66 का कौनसा पद 40 होगा
(A) 16वाँ
(B) 15वाँ
(C) 17वाँ
(D) 20वाँ
उत्तरः
(C) 17वाँ

प्रश्न 5.
श्रेढ़ी a + b, a - b, a - 3b, ..... के 22 पदों का योग होगा
(A) 22 (a - 20b)
(B) 22 (20b - a)
(C) 22 (20a - b)
(D) 22 (a - b)
उत्तरः
(A) 22 (a - 20b)

प्रश्न 6.
श्रेढ़ी - 4, - 1, 2, 5, ..... का 10वाँ पद है
(A) 23
(B) - 23
(C) 32
(D) - 32
उत्तरः
(A) 23

प्रश्न 7.
समान्तर श्रेढ़ी 7, 10, 13, ......, 43 में पदों की संख्या है-
(A) 13
(B) 12
(C) 17
(D) 11
उत्तरः
(A) 13

प्रश्न 8.
यदि किसी समान्तर श्रेढ़ी का प्रथम पद 5, अन्तिम पद 45.तथा पदों का योगफल 400 हो, तो पदों की संख्या होगी
(A) 8
(B) 10
(C) 16
(D) 20
उत्तरः
(C) 16

अतिलघूत्तरात्मक प्रश

प्रश्न 1.
समान्तर श्रेढ़ी 3, 7, 11, 15, ......... का कौनसा पद 499 होगा?
हल:
a = 3, d = 7 - 3 = 4,
a_n = 499
अब a_n = a + (n - 1) × d
⇒ 499 = 3 + (n - 1) × 4
⇒\( \frac{496}{4}\) = n - 1
⇒ 124 = n - 1
∴ n = 124 + 1 = 125

प्रश्न 2.
समान्तर श्रेढ़ी 18, 16, 14,..... के कितने पद लिए जाएँ कि योगफल शून्य हो।
हल:
माना n पद लिये जायें
a = 18, d = 16 - 18 = - 2,
S_n = 0 (दिया है।)
S_n = \(\frac{n}{2}\) (2a + (n – 1) a)
0 = \(\frac{n}{2}\) [2 × 18 + (n - 1) × (- 2)]
⇒ 0 = 36 - 2n + 2
⇒ 2n = 38
∴ n = \(\frac{38}{2}\) = 19

प्रश्न 3.
श्रेढ़ी a + b, a - b, a-3b का 20 पदों का योग बताइए।
हल:
दिया गया है
प्रथम पद (A) = a + b
सार्व अन्तर (d) = a - b - a - b
= - 2b
अब S₂₀ = \(\frac{20}{2}\)[2(a + b) + (20 - 1) × (- 2b)]
= 10(2a + 2b - 40b + 2b)
= 10(2a - 36b) = 20(a - 18b)

प्रश्न 4.
समान्तर श्रेढ़ी 1, - 2, - 5, - 8, ..... का सार्व अन्तर तथा अगले तीन पद लिखिए।
हल:
सार्व अन्तर (d) = - 2 - 1 = - 3
अगले पद a₅ = - 11, a₆ = - 14, a₇ = - 18

प्रश्न 5.
समान्तर श्रेढ़ी 8, 6, 4, ..... का 9 पदों तक योग ज्ञात कीजिए।
हल
प्रथम पद (a) = 8
सार्व अन्तर (d) = 6 - 8 = - 2
S_n = \(\frac{n}{2}\)[2a + (n - 1) d]
∴ S₉ = \(\frac{9}{2}\)[2 × 8 + (9 - 1) × (-2)]
= \(\frac{9}{2}\) [16 - 16] = 0

प्रश्न 6.
यदि दो संख्याओं a तथा b के मध्य n समान्तर माध्य प्रविष्ट किए जाएँ तो सार्व अन्तर d का मान बताइए।
उत्तर:
d = \(\frac{b-a}{n+1}\)

प्रश्न 7.
समान्तर श्रेढ़ी में वे तीन संख्याएँ ज्ञात कीजिए जिनका योगफल-3 और गुणनफल 8 है।
हल:
समान्तर श्रेढ़ी के तीन पद a + d, a, a - d होंगे।
प्रश्नानुसार a + d + a + a - d = - 3 .
a = - 1
(a + d) × a × (a - d) = 8
(- 1 + d) × (- 1) (- 1 - d) = 8
⇒ (1 + d) (d - 1) = 8
∴ d² - 1 = 8
d² = 9 या d= ± 3
अतः वे संख्याएँ 2, - 1, - 4 होंगी।

प्रश्न 8.
समान्तर श्रेढ़ी का व्यापक पद ज्ञात करने का सूत्र लिखिए।
उत्तर:
a_n = a + (n - 1) d

प्रश्न 9.
यदि किसी समान्तर श्रेढ़ी का चौथा पद 64 तथा 54वाँ पद - 61 हो, तो उसका सार्व अन्तर कितना होगा?
उत्तर:
प्रश्नानुसार
a₄ = a + 3d
64 = a + 3d .... (1)
इसी प्रकार a₅₄ = a + 53d .
- 61 = a + 53d .... (ii)
समीकरण (i) में से समीकरण (ii) घटाने पर .
125 = - 50d.
d = \(\frac{-125}{50}\) = \(\frac{-5}{2}\) 

प्रश्न 10.
समान्तर श्रेढ़ी के n पदों का योगफल ज्ञात करने का सूत्र लिखिए।
उत्तर:
S_n = \(\frac{n}{2}\) [2a + (n - 1)d]

प्रश्न 11.
किसी समान्तर श्रेढ़ी का तीसरा पद 18 तथा सातवाँ पद 30 हो, तो इसका 15वाँ पद लिखिए।
उत्तर:
प्रश्नानुसार
18 = a₃ = a + 2d .... (i)
30 = a₇ = a + 6d .... (ii)
समीकरण (i) में से समीकरण (ii) घटाने पर
- 12 = - 4d
∴ d = 37
समीकरण (i) से
18 = a + 2 × 3
a₁₅ = a + 14d = 12 + 14 × 3
= 12 + 42 = 54

प्रश्न 12.
a और b का समान्तर माध्य लिखिए।
उत्तर:
समान्तर माध्य = \(\frac{a+b}{2}\)

प्रश्न 13.
m के किस मान के लिए 10, m, -2 समान्तर श्रेढ़ी में होंगे?
हल:
हम जानते हैं यदि तीन संख्याएँ a, b तथा c समान्तर श्रेढ़ी में होती हैं, तब b = \(\frac{a+c}{2}\) होता है।
⇒ m = \(\frac{10+(-2)}{2}\)
= \(\frac{10-2}{2}\) = \(\frac{8}{2}\) = 4
∴ m = 4 उत्तर

प्रश्न 14.
यदि a = 9 -5n एक समान्तर श्रेढी (A.P.) का nवाँ पद है, तो सार्व अन्तर लिखिये।
हल:
दिया गया है:
a_n = 9 - 5n
n = 1, 2, 3, ............. रखने पर
a₁ = 9 - 5(1) = 4
a₂ = 9 - 5(2) = 9 - 10 = - 1
a₃ = 9 - 5(3) = 9 - 15 = - 6
A.P. के लिये सार्व अन्तर
(d) = a₂ - a₁ = a₃ - a₂
∴ d = - 1 - 4 = - 5

प्रश्न 15.
समान्तर श्रेढ़ी 4, 1, -2, -5 ..... के अगले दो पद लिखिए।
हल:
दी गई श्रेढ़ी 4, 1, -2, -5 ......
श्रेढ़ी का सार्वअन्तर d = 1 - 4 = - 3
अतः 5वाँ पद
(a₅) = - 5 + (-3) = - 5 - 3 = - 8
6ठा पद (a₆) = - 8 + (-3)= - 8 - 3 = - 11
अर्थात् a₅ = - 8 व a₆ = -11

प्रश्न 16.
समान्तर श्रेढ़ी 7, 5, 3, 1, -1, -3,...... का सार्व अन्तर ज्ञात कीजिए।
हल:
समान्तर श्रेढ़ी 7, 5, 3, 1, -1, -3, .....
∵ सार्वअन्तर = a₂ - a₁
यहाँ a₁ = 7, a₂ = 5
∴ सार्वअन्तर (d) = 5 - 7 = -2

प्रश्न 17.
A.P. -17, -12, -7, ................. में 11वाँ पद ज्ञात कीजिए।
हल:
यहाँ a = -17, d = -12 - (-17) = -12 + 17 = 5
और n = 11 चूँकि a = a + (n - 1)d है
इसलिए - a = -17 + (11 - 1) × 5
= - 17 + 10 × 5
= -17 + 50 = 33
अतः दी हुई A.P. का 11वाँ पद 33 है।

लघूत्तरात्मक प्रश्न

प्रश्न 1.
A.P. : 2, 7, 12, ..... का 10वाँ पद ज्ञात कीजिए।
हल:
यहाँ a = 2,d = 7 - 2 = 5 और n = 10 है।
चूँकि a_n = a + (n - 1) d है, इसलिए ।
a₁₀ = 2 + (10 - 1) × 5 = 2 + 45 = 47
अतः दी हुई A.P. का 10वाँ पद 47 है।

प्रश्न 2.
वह A.P. निर्धारित कीजिए जिसका तीसरा पद 5 और 7वाँ पद 9 है।
हल:
प्रश्नानुसार,
a₃ = a + (3 - 1)d = a + 2d = 5 ..... (1)
और a₇ = a + (7 - 1) d = a + 6d = 9 .....(2)
समीकरणों (1) और (2) के युग्म को हल करने पर,
a = 3, d = 1
अतः वांछित A.P. : 3, 4, 5, 6, 7, ..... है।

प्रश्न 3.
28 पदों वाली समान्तर श्रेढ़ी 7, 16, 25, 34, ..... का अन्तिम पद ज्ञात कीजिए।
हल:
दिया हुआ है : प्रथम पद (a) = 7
सार्व अन्तर (d) = 16 - 7 = 9
ज्ञात करना है अन्तिम पद अर्थात् 28वाँ पद = a₂₈
सूत्-
a_n = a + (n - 1) d
a₂₈ = 7 + (28 - 1) 9
= 7 + (27 × 9)
= 7 + 243 = 250
अतः अन्तिम पद = 250

प्रश्न 4.
17 पदों वाली समान्तर श्रेढ़ी 18, 16, 14, 12, ..... का अन्तिम पद ज्ञात कीजिए।
हल:
दिया हुआ है: प्रथम पद (a) = 18,
सार्व अन्तर (d) = 16 - 18 = (-2)
ज्ञात करना है-अन्तिम पद अर्थात् 17वाँ पद = a₁₇
सूत्र a_n = a + (n - 1) d
a₁₇ = 18 + (17 - 1) (-2)
= 18 + [16 × (-2)]
= 18 - 32 = - 14
अतः अन्तिम पद = (- 14)

प्रश्न 5.
दो अंकों वाली कितनी संख्याएँ 3 से विभाज्य हैं?
हल:
3 से विभाज्य होने वाली दो अंकों की संख्याओं की सूची है: 12, 15, 18, ....., 99 .
क्या यह एक A.P. है? हाँ, यह है। यहाँ a = 12,d = 3 तथा a_n = 99 है।
चूंकि a_n = a + (n - 1) d
इसलिए 99 = 12 + (n - 1) × 3 अर्थात्
87 = (n - 1) × 3
अर्थात् n - 1 = \(\frac{87}{3}\) = 29
n = 29 + 1 = 30
अतः, 3 से विभाज्य दो अंकों वाली 30 संख्याएँ हैं। उत्तर

प्रश्न 6.
किसी समान्तर श्रेढ़ी के 11 पदों का योगफल ज्ञात कीजिए जबकि उसके प्रथम व अन्तिम पद का योग 40 है।
हल:
दिया हुआ है-
(1) प्रथम व अन्तिम पद का योग (a + 1) = 40
(2) पदों की संख्या n = 11
ज्ञात करना है : 11 पदों का योग (S₁₁).
S_n = \(\frac{n(a+l)}{2}\)
S₁₁ = \(\frac{11(40)}{2}\) = 11 × 20 = 220

प्रश्न 7.
A.P. : 8, 3, - 2,..... के प्रथम 22 पदों का योग ज्ञात कीजिए।
हल:
यहाँ a = 8, d = 3 - 8 = - 5 और n = 22 है। हम जानते हैं कि
S = \(\frac{n}{2}\) [2a + (n - 1)d]
अतः S = \(\frac{22}{2}\) [16 + 21 (- 5)]
= 11 (16 - 105)
= 11 (- 89) = - 979
इसलिए दी हुई A.P. के प्रथम 22 पदों का योग 979 है।

प्रश्न 8.
किसी समान्तर श्रेढ़ी का nवाँ पद 2n + | 5 है तो श्रेढ़ी के सात पदों का योगफल ज्ञात कीजिये।
हल:
चूँकि दिया गया है :
a_n = 2n + 5
n = 1, 2, 3 .............. रखने पर
a₁ = 2 × 1 + 5 = 2 + 5 = 7
a₂ = 2 × 2 + 5 = 4 + 5 = 9
a₃ = 2 × 3 + 5 = 6 + 5 = 11
∴ श्रेढ़ी होगी
7, 9, 11 .......
∴ d = a₂ - a₁ = 9 - 7 = 2.
∴ S_n = \(\frac{n}{2}\)[2a + (n - 1) d]
= \(\frac{7}{2}\) [2 × 7 + (7 - 1) × 2]
= \(\frac{7}{2}\) [14 + 12] = \(\frac{7}{2}\) × 26
= 7 × 13 = 91

प्रश्न 9.
समान्तर श्रेढ़ी 2, 7, 12, ....... का 11वाँ - पद ज्ञात कीजिए।
हल:
यहाँ a = 2, d = 7 - 2 = 5 और n = 10 है।
∵ a_n = a + (n - 1)d अतः.
a₁₁ = 2 + (11 - 1) × 5 = 2 + 50 = 52
अतः दी हुई समान्तर श्रेढ़ी का 11वाँ पद 52 है।

प्रश्न 10.
यदि किसी A.P. के प्रथम 12 पदों का योग 468 है तथा इसका सार्वअन्तर 6 है तो 10वाँ पद ज्ञात कीजिए।
हल:
प्रश्नानुसार यहाँ S₁₂ = 468, n = 12 तथा सार्वअन्तर (d) = 6
∵ S_n = \(\frac{n}{2}\)[2a + (n - 1)d]
⇒ 468 = \(\frac{12}{2}\) [2a+ (12-1) 6]
या 468 = 6 [2a + 66]
या 2a + 66 = 468 = 78
या 2a = 78 - 66 = 12
∴ a = \(\frac{12}{2}\) = 6
अब 10वाँ पद a₁₀ = a + (n - 1) d
= 6 + (10 - 1) 6
= 6 + 9 × 6
= 6 + 54
= 60
अर्थात् 10वाँ पद 60 है। उत्तर

प्रश्न 11.
A.P. : 17, 15, 13, ..... के कितने पद लिए जाएँ ताकि उनका योग 81 हो?
हल:
प्रश्नानुसार A.P. 17, 15, 13, .....
यहाँ a = 17, d = 15 - 17 = - 2 तथा S_n = 81
∴ \(\frac{n}{2}\)[2a + (n - 1)d] = 81
या \(\frac{n}{2}\)[2(17) + (n - 1) (-2)] = 81
या \(\frac{n}{2}\)[34 - 2n + 2] = 81
या \(\frac{n}{2}\)[-2n + 36] = 81
या n[- n + 18]= 81
या - n² + 18n - 81 = 0
या n² - 18n + 81 = 0
n² - 9n - 9n + 81 = 0
n (n - 9) - 9 (n - 9) = 0
(n - 9) (n - 9) = 0
(n - 9)² = 0
या n = 9
अर्थात् A.P. का योग 81 प्राप्त करने के लिए 9 पद लिए जायें।

निबन्धात्मक प्रश्न

प्रश्न 1.
A.P. : 21, 18, 15, ..... का कौनसा पद -81 है? साथ ही क्या इस A.P. का कोई पद शून्य है? सकारण उत्तर दीजिए।
हल:
यहाँ, a = 21, d = 18 - 21 = - 3 और a. = - 81 है। हमें n ज्ञात करना है।
चूँकि a = a + (n - 1)d
अतः - 81 = 21 + (n - 1) (- 3)
या - 81 = 24 - 3n .
या - 105 = - 3n
अतः n = 35
इसलिए दी हुई A.P. का 35वाँ पद - 81 है।
अब, हम यह जानना चाहते हैं कि क्या कोई n ऐसा है कि a_n = 0 हो। यदि ऐसा कोई n है तो
21 + (n - 1) (-3) = 0
अर्थात् 3 (n - 1) = 21
या n = 8
अतः, 8वाँ पद 0 है।

प्रश्न 2.
क्या संख्याओं की सूची 5, 11, 17, 23, .......... का कोई पद 301 है? क्यों?
हल:
हमें प्राप्त है :
a₂ - a₁ = 11 - 5 = 6, a₃ - a₂ = 17 - 11 = 6, a₄ - a₃ = 23 - 17 = 6
चूँकि k = 1, 2, 3, आदि के लिए a_k+1 - a_k एक समान संख्या होती है, इसलिए दी हुई सूची एक A.P. है।
यहाँ , a = 5 और d = 6
मान लीजिए इस A.P. का nवाँ पद 301 है।
हम जानते हैं कि
a_n = a + (n - 1) d
इसलिए 301 = 5 + (n - 1) × 6
अर्थात् 301 = 6n - 1
अतः n = \(\frac{302}{6}\) = \(\frac{151}{3}\)
परन्तु n एक धनात्मक पूर्णांक होना चाहिए। अतः, 301 संख्याओं की दी हुई सूची का पद नहीं है।

प्रश्न 3.
यदि एक समान्तर श्रेढ़ी का pवाँ पद \(\frac{1}{q}\) है तथा 4 वाँ पद \(\frac{1}{p}\) है, तो सिद्ध कीजिये कि प्रथम pq पदों का योग \(\frac{1}{2}(pq + 1)\) होना चाहिए। हल:
माना समान्तर श्रेढ़ी का प्रथम पद A तथा सार्व अन्तर d है।
∴प्रश्नानुसार
a_p = A + (p - 1)d = \(\frac{1}{q}\) .... (i)
तथा a_q = A + (q - 1)d \(\frac{1}{p}\) ... (ii)
समीकरण (ii) में से (i) को घटाने पर।

प्रश्न 4.
यदि किसी A.P. के प्रथम 14 पदों का योग 1050 है तथा इसका प्रथम पद 10 है तो 20वाँ पद ज्ञात कीजिए।
हल:
यहाँ S₁₂ = 1050, n = 14 और a = 10 है।
चूँकि S_n = \(\frac{n}{2}\)[2a + (n - 1) d]
इसलिए 1050 = \(\frac{14}{2}\)[20 + 13d] = 140 + 91d
अर्थात् 910 = 91d
या d = 10
अतः a = 10 + (20 - 1) × 10 = 200
अर्थात् 20वाँ पद 200 है।

प्रश्न 5.
A.P. : 24, 21, 18, ..... के कितने पद लिए जाएँ, ताकिं उनका योग 78 हो?
हल:
यहाँ a = 24, d = 21 - 24 = - 3 और S_n = 78 है। हमें n ज्ञात करना है।
हम जानते हैं कि S_n = \(\frac{n}{2}\)[2a + (n - 1) d]
78 = \(\frac{n}{2}\) [48 + (n- 1) (-3)]
= \(\frac{n}{2}\) [51 - 3n]
या 3n² - 51n + 156 = 0
या n² - 17n + 52 = 0
या n² - 4n - 13n + 52 = 0
या n (n - 4) - 13 (n - 4) = 0
या (n - 4) (n - 13) = 0
अतः n = 4 या 13
n के ये दोनों मान सम्भव हैं और स्वीकार किए जा सकते हैं। अतः, पदों की वांछित संख्या या तो 4 है या 13 है।

प्रश्न 6.
निम्नलिखित का योग ज्ञात कीजिए:
(i) प्रथम 1000 धन पूर्णांक
(ii) प्रथम n धन पूर्णांक।
हल:
(i) मान लीजिए S = 1 + 2 + 3 + ..... + 1000 है।
A.P. के प्रथम n पदों के योग के सूत्र S_n = \(\frac{n}{2}\)(a + l) का प्रयोग करने पर
S₁₀₀₀ = \(\frac{1000}{2}\) (1 + 1000)
= 500 × 1001 = 500500
अतः, प्रथम 1000 धन पूर्णांकों का योग 500500 है।

(ii) मान लीजिए S_n = 1 + 2 + 3 + ..... + n है।
यहाँ a = 1 और अन्तिम पद l = n है।
अतः S_n = \(\frac{n(1+n)}{2}\) या S_n = \(\frac{n(n+1)}{2}\)

प्रश्न 7.
1000 रु. की एक धनराशि 8% वार्षिक साधारण ब्याज पर निवेश की जाती है। प्रत्येक वर्ष के अन्त में ब्याज परिकलित कीजिए। क्या ये ब्याज एक A.P. बनाते हैं? यदि ऐसा है, तो इस तथ्य का प्रयोग करते हुए 30 वर्षों के अन्त में ब्याज परिकलित कीजिए।
हल:
हम जानते हैं कि साधारण ब्याज परिकलित करने के लिए सूत्र निम्नलिखित है:
साधारण ब्याज = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}\)
अतः प्रथम वर्ष के अन्त में ब्याज = \(\frac{1000 \times 8 \times 1}{100}\) = 80 रु.
दसरे वर्ष के अन्त में ब्याज \(\frac{1000 \times 8 \times 2}{100}\) रु. = 160 रु.
तीसरे वर्ष के अन्त में ब्याज \(\frac{1000 \times 8 \times 3}{100}\) रु. = 240 रु.
इसी प्रकार, हम चौथे, पाँचवें, इत्यादि वर्षों के अन्त में ब्याज परिकलित कर सकते हैं।
अतः, पहले, दूसरे, तीसरे, ..... वर्षों के अन्त में ब्याज (रुपयों में) क्रमशः हैं :
80, 160, 240, .....
यह एक A.P. है, क्योंकि किन्हीं दो क्रमागत पदों का अंन्तर 80 है, अर्थात् d = 80 है। साथ ही, इसमें a = 80 है।
अतः, 30 वर्षों के अन्त में ब्याज ज्ञात करने के लिए हम an ज्ञात करेंगे।
अब a₃₀ = a + (30 - 1) d = 80 + 29 × 80 = 2400
अत: 30 वर्षों के अन्त में ब्याज 2400 रु. होगा। 

प्रश्न 8.
फूलों की एक क्यारी की पहली पंक्ति में 23 गुलाब के पौधे हैं, दूसरी पंक्ति में 21 गुलाब के पौधे हैं, तीसरी पंक्ति में 19 गुलाब के पौधे हैं, इत्यादि। उसकी अन्तिम पंक्ति में 5 गुलाब के पौधे हैं। इस क्यारी में कुल कितनी पंक्तियाँ हैं?
हल:
पहली, दूसरी, तीसरी, ...... पंक्तियों में गुलाब के पौधों की संख्याएँ क्रमशः 23,21, 19,.....,5 हैं । ये एक A.P. बनाती हैं। माना कि पंक्तियों की संख्या n है।
अतः a = 23, d = 21 - 23 = - 2 तथा a = 5
∵ a_n = a + (n - 1) d
∴ 5 = 23 + (n - 1) ( - 2)
या - 18 = (n - 1) (- 2)
या n = 10
अतः फूलों की क्यारी में 10 पंक्तियाँ हैं।

प्रश्न 9.
संख्याओं की उस सूची के प्रथम 24 पदों | का योग ज्ञात कीजिए, जिसका nवाँ पद a_n = 3 + 2n से दिया जाता है।
हल:
चूँकि a_n = 3 + 2n है इसलिए
a₁ = 3 + 2 = 5
a₂ = 3 + 2 × 2 - 7
a₃ = 3 + 2 × 3 = 9
इस प्रकार प्राप्त संख्याओं की सूची 5, 7, 9, 11, ..... है।
यहाँ 7 - 5 = 9 - 7 = 11 - 9 = 2 इत्यादि हैं।
अतः इनसे एक A.P. बनती है, जिसका सार्व अन्तर 12 है।
S₂₄ ज्ञात करने के लिए यहाँ n = 24, a = 5, d = 2
अतः S₂₄ = \(\frac{24}{2}\) [2 × 5 + (24 - 1) × 2]
= 12 [10 + 46] = 672
इसलिए संख्याओं की दी हुई सूची के प्रथम 24 पदों का योग 672 है।

प्रश्न 10.
टी.वी. सेटों का निर्माता तीसरे वर्ष में 1600 टी.वी. तथा 7वें वर्ष में 700 टी.वी. सेटों का उत्पादन करता है। यह मानते हुए कि प्रत्येक वर्ष उत्पादन में एक समान रूप से एक निश्चित संख्या में वृद्धि होती है, ज्ञात कीजिए:
(i) प्रथम वर्ष में उत्पादन
(ii) 10वें वर्ष में उत्पादन
(iii) प्रथम 7 वर्षों में कुल उत्पादन।
हल:
(i) चूँकि प्रत्येक वर्ष उत्पादन में समान रूप से एक निश्चित संख्या में वृद्धि होती है, इसलिए पहले, दूसरे, तीसरे, ....... वर्षों में उत्पादित टी.वी. सेटों की संख्याएँ एक A.P. में होंगी। यदि nवें वर्ष में उत्पादित टी.वी. सेटों की संख्या को a,sub>n से व्यक्त करें, तो
अतः a₃ = 600 और a₇ = 700
या a + 2d = 600
और a + 6d = 700
इन्हें हल करने पर, हमें d = 25 और a = 550 प्राप्त होता है।
अतः प्रथम वर्ष में उत्पादित टी.वी. सेटों की संख्या 550 है।

(ii) अब a₁₀ = a + 9d = 550 + 9 × 25 = 550 + 225 = 775
अतः 10वें वर्ष में उत्पादित टी.वी. सेटों की संख्या 775 है।

(iii) साथ ही S₇ = \(\frac{7}{2}\) [2 × 550 + (7 - 1) 25]
= \(\frac{7}{2}\) [1100 + 150]
= 4375
अतः प्रथम 7 वर्षों में कुल उत्पादित हुए सभी टी.वी. सैटों की संख्या 4375 है।

प्रश्न 11.
1 से 100 तक के मध्य की 6 से विभाजित होने वाली संख्याओं का योगफल ज्ञात कीजिये।
हल:
1 से 100 तक के मध्य की 6 से विभाजित होने वाली धन पूर्णांकों की सूची 6, 12, 18, 24, 30, ..........., 96
उपर्युक्त संख्याएँ समान्तर श्रेढ़ी क्रम में हैं। प्रथम पद a = 6 तथा सार्व अन्तर d = 12 - 6 = 6.
अन्तिम पद a, = 96
पदों का योग S_n = ?
अब a_n = a + (n - 1)d
96 = 6 + (n - 1) × 6
⇒ 96 - 6 = (n - 1) × 6
⇒ 90 = (n - 1) × 6
⇒ (n - 1) = \(\frac{90}{6}\) = 15
⇒ ∴ n = 15 + 1 = 16
हम जानते हैं S_n = \(\frac{n}{2}\)(a + a_n)
∴ S₁₆ = \(\frac{16}{2}\)(6 + 96)
= \(\frac{16 \times 102}{2}\) = 8 × 102 = 816

प्रश्न 12.
उस A.P. के प्रथम 15 पदों का योग ज्ञात कीजिए जिसका पाँचवाँ और नवाँ पद क्रमशः 26 और 42 है।
हल:
माना कि 'a' और 'd प्रथम पद और सार्वअन्तर है।
दिया गया है कि a₅ = 26, a₉ = 42
Ss = ?, n = 15
प्रश्नानुसार a₅ = a + (5 - 1)d
26 = a + 4d
a₉ = a + (9 - 1)d
42 = a + 8d ....(2)
समीकरण (1) - समीकरण (2)
26 - 42 = a + 4d - a - 8d
⇒ -16 = - 4d
∴ d = \(\frac{-16}{-4}\) = 4
d का मान समी. (1) में रखने पर
26 = a + 4 × 4
6 = a + 16.
∴ a = 26 - 16 = 10
s_n = \(\frac{n}{2}\)[2a + (n - 1)4]
मान रखने पर