RBSE Class 10 Maths Important Questions Chapter 11 रचनाएँ

Rajasthan Board RBSE Class 10 Maths Important Questions Chapter 11 रचनाएँ Important Questions and Answers.

RBSE Class 10 Maths Chapter 11 Important Questions रचनाएँ

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
किस स्थिति में त्रिभुज की रचना नहीं की जा | सकती
(A) यदि तीनों कोण दिए हों।
(B) यदि तीन भुजाएँ दी हों।
(C) दो कोण व एक भुजा दी हों।
(D) दो भुजाएँ व उनके मध्य का कोण दिया हो।
उत्तरः
(A) यदि तीनों कोण दिए हों।

प्रश्न 2.
एक रेखाखण्ड को दिए हुए अनुपात में विभाजित करने के लिए रेखाखण्ड के एक बिन्दु पर बनाया जाता है
(A) वृहत् कोण
(B) अधिक कोण
(C) समकोण
(D) न्यूनकोण
उत्तरः
(D) न्यूनकोण

प्रश्न 3.
वह रेखाखण्ड जो वृत्त के केन्द्र से गुजरता है और जिसके दोनों सिरे वृत्त पर स्थित हों, कहलाता है
(A) त्रिज्या
(B) व्यास
(C) त्रिज्याखण्ड
(D) वृत्तखण्ड
उत्तरः
(B) व्यास

प्रश्न 4.
ऐसी सरल रेखा जो वृत्त की परिधि को केवल एक ही बिन्दु पर स्पर्श करती है, कहते हैं
(A) छेदन रेखा
(B) स्पर्श रेखा
(C) समद्विबाहु रेखा
(D) विभक्त रेखा
उत्तरः

प्रश्न 5.
वृत्त के बाहर स्थित बिन्दु से खींची गई स्पर्श रेखाओं की संख्या हो सकती है
(A) 2
(B) 3
(C) 0
(D) 4
उत्तरः
(A) 2

प्रश्न 6.
दिए गए चित्र में स्पर्श रेखा है-

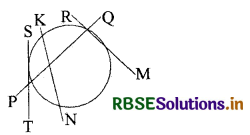
(A) PQ
(B) ST
(C) PM
(D) KN
उत्तरः
(B) ST

प्रश्न 7.
दिए गए चित्र में स्पर्श रेखाओं की संख्या है-

(A) 4
(B) 5
(C) 6
(D) 7
उत्तरः
(D) 7

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
दो वृत्त एक-दूसरे को अन्तः स्पर्श करते हैं, तो उनकी उभयनिष्ठ स्पर्श रेखाओं की संख्या लिखिये।
उत्तर:
एक।

प्रश्न 2.
एक वृत्त में अधिक से अधिक कितनी जीवाएँ खींची जा सकती हैं?
उत्तर:
अनन्त जीवाएँ।

प्रश्न 3.
वृत्त के बाहर स्थित किसी बिन्दु से कितनी स्पर्श रेखाएँ खींची जा सकती हैं?
उत्तर:
दो।

प्रश्न 4.
वृत्त की छेदन रेखा PQ है। छेदन रेखा PQ के स्पर्श रेखा बनने का प्रतिबन्ध लिखिए।
उत्तर:
जब बिन्दु P व Q सम्पाती हों अर्थात् दोनों एक ही बिन्दु हों तो छेदन रेखा PQ स्पर्श रेखा कहलाएगी।

प्रश्न 5.
वृत्त की स्पर्श रेखा व त्रिज्या में क्या सम्बन्ध होता है?
उत्तर:
वृत्त के स्पर्श बिन्दु से खींची गई त्रिज्या एवं स्पर्श रेखा एक-दूसरे पर लम्ब होती है।

प्रश्न 6.
किसी बाह्य बिन्दु से वृत्त पर खींची गयी स्पर्श रेखा की लम्बाई 12 सेमी. है, यदि वृत्त की त्रिज्या 5 सेमी. तो केन्द्र से बाह्य बिन्दु की दूरी ज्ञात कीजिये।
उत्तर:
दूरी = \(\sqrt{(12)^{2}+(5)^{2}}\)
= \(\sqrt{144+25}\)
= √169
= 13 सेमी.

प्रश्न 7.
दिए गए चित्र में छेदन रेखा का नाम लिखिए।

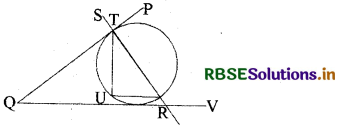
उत्तर:
छेदन रेखा = SR

प्रश्न 8.
दिए ए चित्र में स्पर्श रेखाओं की संख्या लिखिए।

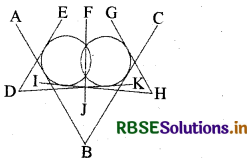
हल:
स्पर्श रेखाएँ—ED, DK, AB, BC, HG व HI हैं।
अतः कुल संख्या = 6

प्रश्न 9.
3 सेमी. त्रिज्या वाले वृत्त पर स्थित किसी बिन्दु पर स्पर्श रेखा की रचना कीजिए।
हल:

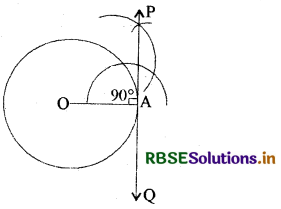
लघूत्तरात्मक एवं निबन्धात्मक प्रश्न

प्रश्न 1.
एक त्रिभुज ABC की रचना कीजिए जिसकी भुजाएँ 7.5 सेमी., 7 सेमी. और 6.5 सेमी. हों। ∆ABC के समरूप एक त्रिभुज की रचना कीजिए जिसकी प्रत्येक भुजा ∆ABC की संगत भुजा का \(\frac{2}{3}\) वाँ भाग हो।
हल:
रचना के चरण:
(i) BC = 7.5 सेमी. की रेखा खींची।
(ii) B से BA = 6.5 सेमी. तथा C से CA = 7.0 सेमी. के चाप काटे जो A बिन्दु पर मिलते हैं। इन्हें मिलाने से ∆ABC प्राप्त हुआ।
(iii) BC के बिन्दु B पर कोई कोण बनाती हुई रेखा BX खींची।
(iv) BX को B से प्रारम्भ कर 1 सेमी. के 3 बराबर भागों में बाँटा। तीसरे भाग का शीर्ष D है। D को C से मिलाया।

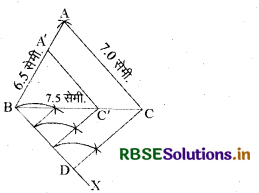
(v) परकार की सहायता से BD के प्रत्येक बिन्दु से ∠BDC के बराबर कोण बनाते हुए रेखाएँ खींची जो BC पर मिलती हैं। इस प्रकार BC के भी तीन बराबर भाग प्राप्त हुए।
(vi) BC के तीन बराबर भागों में से दूसरे भाग के शीर्ष पर C' अंकित किया।
(vii) C' से CA के समान्तर रेखा खींची जो BA को A' पर मिले।
इस प्रकार ∆A'BC' त्रिभुज ABC के समरूप प्राप्त होगा।

प्रश्न 2.
3.2 सेमी. त्रिज्या का एक वृत्त खींचिये। इसके दो बिन्दुओं पर 70° का कोण बनाती हुई दो त्रिज्याएँ खींचिए। ये त्रिज्याएँ जहाँ वृत्त को मिलें, उन बिन्दुओं पर वृत्त की स्पर्श रेखाएँ खींचिए।
हल:
रचना के चरण : 3.2 सेमी. की त्रिज्या का | वृत्त खींचकर इसके केन्द्र पर 70° का कोण POQ बनाया।
Q व P बिन्दु पर समकोण की रचना करने पर हमें स्पर्श रेखाएँ RP व RQ प्राप्त होंगी।

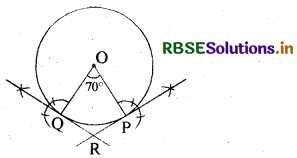
प्रश्न 3.
AB = 5 सेमी. लम्बाई का एक रेखाखण्ड का वृत्त बनाइए तथा इस वृत्त पर बिन्दु A से स्पर्श रेखाएँ खींचिए।
हल:
रचना: (i) एक रेखा AB = 5 सेमी. की खींची। बिन्दु B पर 2.2 सेमी. त्रिज्या का एक वृत्त खींचा।
(ii) AB का मध्य बिन्दु 0 प्राप्त किया तथा 0 को केन्द्र मानकर OA त्रिज्या का एक वृत्त खींचा। यह वृत्त पहले वाले वृत्त को P व Q बिन्दु पर काटता है। P व Q को A से मिलाकर स्पर्श रेखा PA व AQ प्राप्त की।

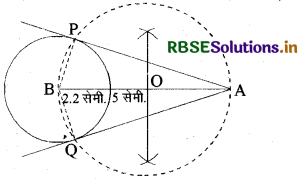
प्रश्न 4.
एक त्रिभुज PQR की रचना कीजिए जिसमें PQ = 6 सेमी., ∠Q = 70° तथा QR = 5.7 सेमी. हैं। इसे एक समरूप त्रिभुज में बदलिए जिसकी भुजाएँ तथा ∆PQR की संगत भुजाओं का अनुपात \(\frac{3}{5}\) में हो। रचना के प्रमुख पद लिखिए।
हल:
रचना:
(i) दिया गया त्रिभुज PQR बनाया।
(ii) QR के बिन्दु Q पर कोई कोण बनाती हुई रेखा QX खींची।

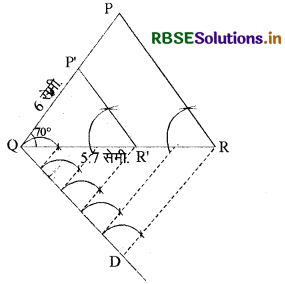
(iii) QX को Q से प्रारम्भ कर एक-एक सेमी. के पाँच बराबर भागों में बाँटा। पाँचवें भाग का शीर्ष D है। D को R से मिलाया।
(iv) परकार की सहायता से QD के प्रत्येक बराबर भाग ∠QDR के बराबर कोण बनाते हुए रेखाएँ खींची जो OR पर मिलती हैं। ये QR के भी पाँच बराबर भाग हैं।
(v) QR के पाँच बराबर भागों में से तीसरे भाग के शीर्ष पर R' अंकित किया।
(vi) R' से RP के समान्तर रेखा खींची जो OP को P' पर मिलती है।
अतः इस प्रकार ∆PQR', ∆POR के समरूप त्रिभुज है।

प्रश्न 5.
एक दिए गए त्रिभुज ABC के समरूप एक त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए गए त्रिभुज की संगत भुजाओं की \(\frac{3}{4}\) हों (अर्थात् स्केल गुणक \(\frac{3}{4}\) है।)
हल:
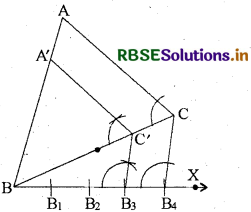
एक त्रिभुज ABC दिया है। हमें एक अन्य त्रिभुज की रचना करनी है, जिसकी भुजाएँ त्रिभुज ABC की संगत भुजाओं की \(\frac{3}{4}\) हों।
रचना :

• सर्वप्रथम BC से शीर्ष A की दूसरी ओर न्यूनकोण बनाती हुई एक किरण BX खींचिए।
• अब BX पर 4 बिन्दु (\(\frac{3}{4}\) में 3 और 4 में से बड़ी संख्या) B₁, B₂, B₃ और B₄, इस प्रकार अंकित कीजिए कि BB₁ = B₁B₂ = B₂B₃ = B₃B₄ हो।
• B₄C मिलाइए और B₃ (तीसरे बिन्दु, यहाँ \(\frac{3}{4}\) में 3 और 4 में से 3 छोटी है) से होकर जाने वाली B,C के समान्तर एक रेखा BC को C' पर प्रतिच्छेद करती हुई खींचिए।
• C' से होकर जाने वाली CA के समान्तर एक रेखा BA को A' पर प्रतिच्छेद करती हुई खींचिए।
• तब, ∆A'BC' अभीष्ट त्रिभुज है।

स्पष्टीकरण:
∵ \(\frac{\mathrm{BC}^{\prime}}{\mathrm{C}^{\prime} \mathrm{C}}=\frac{3}{1}\)
इसलिए. \(\frac{\mathrm{BC}}{\mathrm{BC}}=\frac{\mathrm{BC}^{\prime}+\mathrm{C}^{\prime} \mathrm{C}}{\mathrm{BC}}\) = 1 + \(\frac{\mathrm{C}^{\prime} \mathrm{C}}{\mathrm{BC}^{\prime}}\) = 1 + \(\frac{1}{3}\) = \(\frac{4}{3}\),
अर्थात् \(\frac{B C^{\prime}}{B C}\) = \(\frac{3}{4}\)
साथ ही, C'A', CA के समान्तर है। इसलिए ∆A'BC' ~ ∆ABC
अतः, \(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}\) = \(\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}\) = \(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}\) = \(\frac{3}{4}\)

प्रश्न 6.
एक दिए गए त्रिभुज ABC के समरूप एक त्रिभुज की रचना कीजिए, जिसकी भुजाएँ त्रिभुज ABC की संगत भुजाओं की \(\frac{5}{3}\) हों (अर्थात् स्केल गुणक \(\frac{5}{3}\) है)।
हल:
एक त्रिभुज ABC दिया गया है। हमें एक त्रिभुज की रचना करनी है, जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac{5}{3}\) हों।
रचना:
1. सर्वप्रथम BC से शीर्ष A के दूसरी ओर न्यूनकोण बनाती हुई एक किरण BX खींचिए।।

2. 5(\(\frac{5}{3}\) में 5 और 3 में से बड़ी संख्या) बिन्दु B₁, B₂, B₃, B₄ और B₅, BB₁ पर इस प्रकार अंकित कीजिए कि B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ हो।

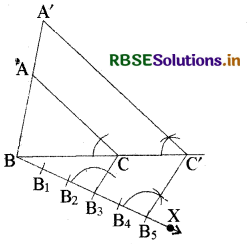
3. अब B₃ (तीसरा बिन्दु, \(\frac{5}{3}\) में 5 और 3 में से छोटी संख्या) को C से मिलाइए और B₅ से होकर जाने वाली B₃C के समान्तर एक रेखा, बढ़ाए गए रेखाखण्ड BC को C' पर प्रतिच्छेद करती हुई खींचिए।

4. C' से होकर जाने वाली CA के समान्तर एक रेखा, बढ़ाने पर रेखाखण्ड BA को A' पर प्रतिच्छेद करती हुई खींचिए।
तब, A'BC' अभीष्ट त्रिभुज है।
स्पष्टीकरण- ∵ ∆ABC ~ ∆A'BC' दसल- AB _ AC _ - BC
इसलिए \(\frac{\mathrm{AB}}{\mathrm{A}^{\prime} \mathrm{B}}=\frac{\mathrm{AC}}{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}=\frac{-\mathrm{BC}}{\mathrm{BC}^{\prime}}\)
परन्तु \(\frac{\mathrm{BC}}{\mathrm{BC}^{\prime}}=\frac{\mathrm{BB}_{3}}{\mathrm{BB}_{5}}=\frac{3}{5}\)
इसलिए \(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}\) = \(\frac{5}{3}\) और इसीलिए \(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}\) = \(\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}\) = \(\frac{B C^{\prime}}{B C^{\prime}}=\frac{5}{3}\)

प्रश्न 7.
8 सेमी. लम्बा एक रेखाखण्ड खींचिए।A को केन्द्र लेकर 4 सेमी. त्रिज्या का एक वृत्त बनाइये तथा बिन्दु B से इस वृत्त पर स्पर्श रेखा युग्मों की रचना कीजिये एवं उनकी लम्बाइयाँ मापिये।
हल:
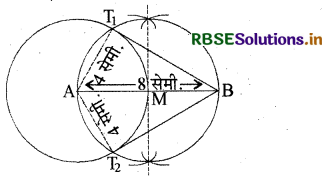
दिया है-रेखाखण्ड AB = 8.0 सेमी. केन्द्र A से 4 सेमी. त्रिज्या का एक वृत्त खींचा गया है।

रचना:

• रेखाखण्ड AB = 8 सेमी. खींचा।
• केन्द्र A से 4 सेमी. त्रिज्या का एक वृत्त खींचा।
• अब हम रेखाखण्ड AB को परकार की सहायता से समद्विभाजित करते हैं। इस तरह से हमें AB का मध्य बिन्दु M प्राप्त होता है।
• केन्द्र M लेकर AB व्यास का एक वृत्त खींचा जो A केन्द्र वाले वृत्त को T₁ व T₂ स्थान पर काटता है।
• रेखाखण्ड T₁B व T₂B खींचे अतः T₁B व T₂B केन्द्र A वाले वृत्त की स्पर्श रेखाएँ हैं और इन्हें नापने पर T₁B = T₂B = 6.9 सेमी. प्राप्त होती है। ।

प्रश्न 8.
7.5 सेमी. रेखाखण्ड को 2 : 3 के अनुपात | में विभाजित कीजिए। केवल चित्र बनाइए।
हल:

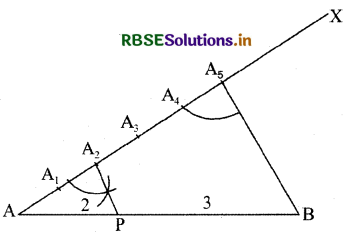
प्रश्न 9.
3 सेमी. त्रिज्या के एक वत्त पर 5 सेमी. त्रिज्या के एक संकेन्द्रीय वृत्त के किसी बिन्दु से एक स्पर्श रेखा की रचना कीजिए और उसकी लम्बाई मापिए।
हल:

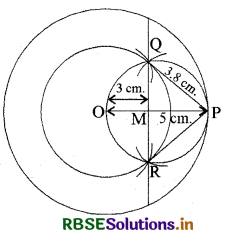
रचना के चरण:

• सर्वप्रथम 0 बिन्दु से 3 cm तथा 5 cm त्रिज्या के दो संकेन्द्री वृत्त बनाए।
• बड़े वृत्त की परिधि पर कोई बिन्दु P अंकित कर दिया।
• अब OP को मिलाकर इस रेखा को समद्विभाजित किया तथा M को इसका माध्य बिन्दु मान लिया।
• अब M को केन्द्र मानकर MP त्रिज्या का एक वृत्त खींचा जो वृत्त को. Q व R पर प्रतिच्छेदित करें।
• अब PQ व PR को मिलाइए और इस प्रकार PQ तथा PR वांछित स्पर्श रेखाएँ होंगी। स्पर्श रेखाओं की लम्बाई = RP = PQ = 3.8 सेमी.

प्रश्न 10.
4 सेमी, 5 सेमी और 6 सेमी भुजाओं वाले एक त्रिभुज की रचना कर इसके समरूप एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ दिये गये त्रिभुज की संगत भुजा की \frac{3}{5} गुना हों।
हल:
रचना के चरण
1. सर्वप्रथम एक रेखाखण्ड 6 cm का खींचिए।
2. अब B को केन्द्र मानकर 5 cm के बराबर त्रिज्या भरकर एक चाप काटिये।
3. C को केन्द्र मानकर 4 cm के बराबर त्रिज्या भरकर पहले वाले चाप को A पर काटते हुए चाप लगाइए।

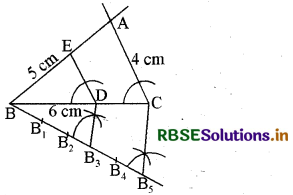
4. AB और AC को मिलाइए। इस प्रकार ∆ABC अभीष्ट त्रिभुज होगा।
5. BC के नीचे एक न्यून कोण CBX बनाइए
6. BX के साथ 5 बिन्दु B₁, B₂, B₃, B₄ और B₅ इस प्रकार अंकित कीजिए कि BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ हो जायें।
7. अब BC को मिलाइए।
8. B₃ से B₃D || B₅C खींचिए जो BC को D पर मिलता है।
9. D से ED || AC खींचिए जो BA को E पर | मिलती है। इस प्रकार ∆EBD अभीष्ट त्रिभुज होगा जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \frac{3}{5} गुनी होंगी।

प्रश्न 11.
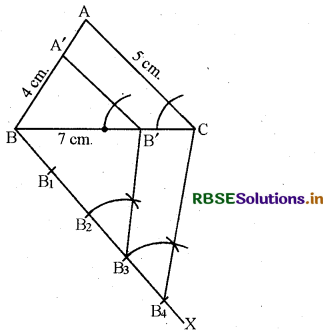
4 cm., 5 cm. और 7 cm. भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की \frac{3}{4} गुनी हों।
हल:
रचना के चरण:

• सर्वप्रथम एक रेखाखण्ड 7 cm. का खींचिये।
• अब B को केन्द्र मानकर 4 cm. के बराबर त्रिज्या भर कर एक चाप काटिये।
• C को केन्द्र मानकर 5 cm. के बराबर त्रिज्या भरकर पहले वाले चाप को A पर काटते हुए चाप लगाइये।
• AB और AC को मिलाइये। इस प्रकार ∆ABC अभीष्ट त्रिभुज होगा।
• BC के नीचे एक न्यून कोण CBX बनाइये।
• BX के साथ 4 बिन्दु B₁, B₂, B₃ और B₄ इस प्रकार अंकित कीजिये कि BB₁ = B₁B₂ = B₂B₃ = B₃B₄ हो जाये।
• अब B,C को मिलाइये।
• B₃ से B₃B || B₄C खींचिये जो BC को B' पर मिलता है।
• B से B'A' || AC खींचिये जो BA को A' पर मिलती है। इस प्रकार ∆A'BC' अभीष्ट त्रिभुज होगा जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \frac{3}{4} गुनी होगी।