RBSE Solutions for Class 8 Maths Chapter 5 आँकड़ो का प्रबंधन Intext Questions

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 5 आँकड़ो का प्रबंधन Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 5 आँकड़ो का प्रबंधन Intext Questions

(पाठगत प्रश्न - पृष्ठ 73-74)

प्रश्न 1.
एक चित्रालेख (pictograph)

(i) जुलाई के महीने में कितनी कारों का उत्पादन हुआ?
हल:
जुलाई के महीने में 250 कारों का उत्पादन हुआ।

(ii) किस महीने में कारों का अधिकतम उत्पादन हुआ?
हल:
सितम्बर महीने में कारों का अधिकतम उत्पादन (400) हुआ।

प्रश्न 2.
एक दण्ड आलेख (bar graph)

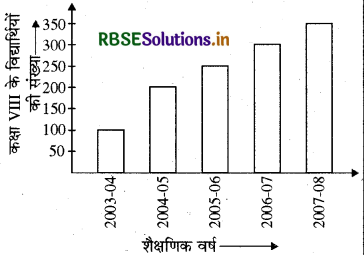
(i) इस दंड आलेख द्वारा क्या सूचना दी गई है?
हल:
दिए गए दंड आलेख द्वारा विभिन्न शैक्षणिक वर्षों में कक्षा VIII में छात्रों की संख्या दी गई है।

(ii) किस वर्ष में विद्यार्थियों की संख्या में अधिकतम वृद्धि हुई?
हल:
वर्ष 2004-05 में विद्यार्थियों की संख्या में अधिकतम वृद्धि हुई।

(iii) किस वर्ष में विद्यार्थियों की संख्या अधिकतम है?
हल:
वर्ष 2007-08 में विद्यार्थियों की संख्या अधिकतम है।

(iv) बताइए कि यह सत्य है या असत्य : "2005-06 में विद्यार्थियों की संख्या 2003-04 की संख्या की दुगुनी है।"
हल:
असत्य।

प्रश्न 3.
द्वि-दंड आलेख (double bar graph)

(i) इस द्वि-दंड आलेख द्वारा क्या सूचना दी गई है?
हल:
इस द्वि-दंड आलेख द्वारा वर्ष 2005-06 और 2006-07 में एक विद्यार्थी के विभिन्न विषयों में प्राप्तांकों की सूचना दी गई है।

(ii) किस विषय में विद्यार्थी के प्रदर्शन में सबसे अधिक सुधार हुआ है?
हल:
गणित विषय में विद्यार्थी के प्रदर्शन में अधिकतम सुधार हुआ है।

(iii) किस विषय में प्रदर्शन में गिरावट आई है?
हल:
अंग्रेजी विषय में प्रदर्शन में गिरावट आई है।

(iv) किस विषय में प्रदर्शन समान रहा है?
हल:
हिन्दी विषय में प्रदर्शन समान रहा है।

(सोचिए, चर्चा कीजिए और लिखिए - पृष्ठ 75)

प्रश्न-यदि हम एक दंड आलेख के दंडों में से किसी एक की स्थिति बदल दें, तो क्या प्रदर्शित जानकारी में कोई बदलाव या परिवर्तन होगा? क्यों?
हल:
नहीं, सूचना में दण्डों की स्थिति बदलने पर कोई बदलाव नहीं होगा। |

(प्रयास कीजिए - पृष्ठ 75)

दी हुई सूचना को निरूपित करने के लिए एक उपयुक्त आलेख खींचिए।

प्रश्न 1.

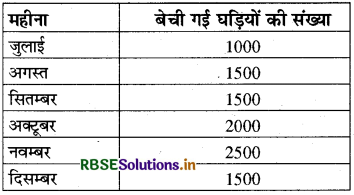
हल:
दिए गए आँकड़ों को दण्ड आलेख पर निरूपित करने के लिए X-अक्ष पर महीना और Y-अक्ष पर बेची गई घड़ियों की संख्या को दर्शाएंगे। चूंकि हमें 6 गणितीय आँकड़े दिए गए हैं, अतः हम क्षैतिज रेखा पर समान दूरी पर 6 बिन्दु लगाएंगे और इन बिन्दुओं पर समान मोटाई के आयत खींचेंगे।

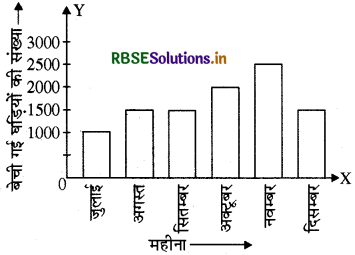
प्रश्न 2.

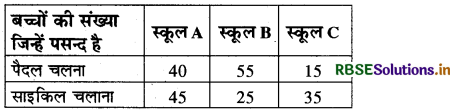
हल:
दिए गए आँकड़ों को दण्ड आलेख द्वारा दर्शाने के लिए X अक्ष पर पसन्द और Y अक्ष पर बच्चों की संख्या लेंगे। स्कूल A, B और C के दोनों बिन्दुओं के आँकड़े दिए गए हैं। अतः क्षैतिज रेखा पर दो बिन्दु लेंगे तथा प्रत्येक बिन्दु पर समान चौड़ाई के तीन आयत खींचेंगे। इनकी ऊँचाई गणितीय आँकड़ों की संगत होगी जैसा कि चित्र में दर्शाया गया है।

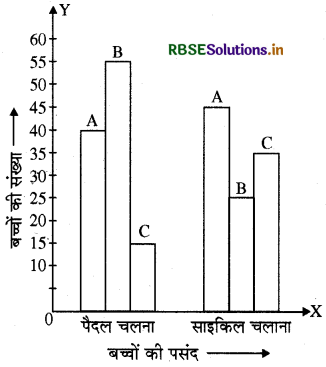
प्रश्न 3.
8 सर्वश्रेष्ठ क्रिकेट टीमों द्वारा ODI में जीतने का प्रतिशत

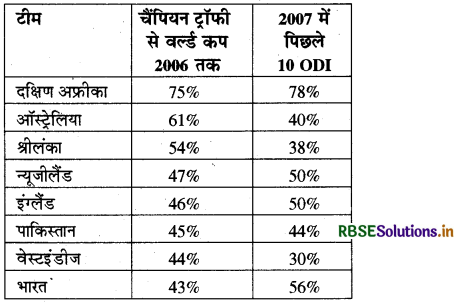
हल:
x-अक्ष पर टीम और Y-अक्ष पर उनकी जीत का प्रतिशत दर्शाते हैं। चैंपियन ट्रॉफी से वर्ल्डकप 2006 तक के प्रतिशत को डॉट लाइन से तथा 2007 में ODI के प्रतिशत को गहरी लाइन से दर्शाते हैं।

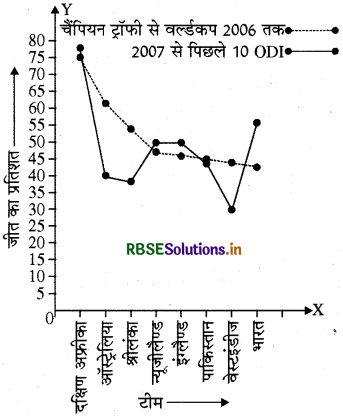
(प्रयास कीजिए - पृष्ठ 76)

प्रश्न 1.
विद्यार्थियों के एक समूह से यह बताने को कहा गया है कि वे किस पशु को सबसे अधिक घर में पालना पसन्द करेंगे। इसके परिणाम नीचे दिए गए हैंकुत्ता, बिल्ली, बिल्ली, मछली, बिल्ली, खरगोश, कुत्ता, बिल्ली, खरगोश, कुत्ता, बिल्ली, कुत्ता, कुत्ता, कुत्ता, बिल्ली, गाय, मछली, खरगोश, कुत्ता, बिल्ली, कुत्ता, बिल्ली, बिल्ली, कुत्ता,खरगोश, बिल्ली, मछली, कुत्ता। उपरोक्त के लिए एक बारम्बारता बंटन सारणी बनाइए।
हल:
हम मिलान चिह्न का प्रयोग करके आँकड़ों को बारम्बारता सारणी में रखेंगे-

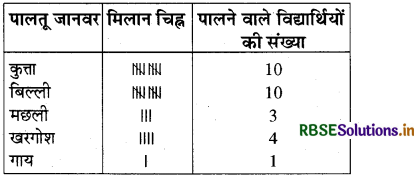
(प्रयास कीजिए - पृष्ठ 78)

प्रश्न 1.
निम्नलिखित बारम्बारता बंटन सारणी का अध्ययन कीजिए और उसके नीचे दिए हुए प्रश्नों के उत्तर दीजिए

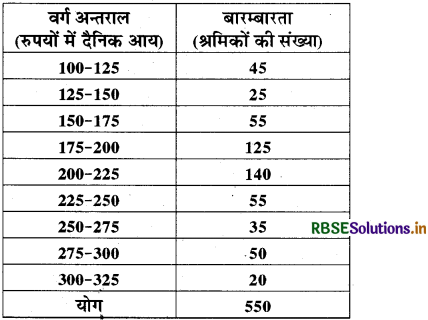
(i) वर्ग अन्तरालों की माप क्या है?
हल:
वर्ग अन्तराल की माप 25 है।

(ii) किस वर्ग की सबसे अधिक बारम्बारता है?
हल:
वर्ग 220-225 की सबसे अधिक बारम्बारता है।

(iii) किस वर्ग की सबसे कम बारम्बारता है?
हल:
वर्ग 300-325 की बारम्बारता सबसे कम है।

(iv) वर्ग अन्तसल 250-275 की उच्च सीमा क्या है?
हल:
वर्ग अंन्तराल 250-275 की उच्च सीमा 275 है।

(v) किन दो वर्गों की बारम्बारता एक ही है?
हल:
वर्ग 150-175 और 225-250 की बारम्बारता एक ही है।

प्रश्न 2.
अन्तरालों 30-35, 35-40 इत्यादि का प्रयोग करते हुए एक कक्षा के 20 विद्यार्थियों के भारों (kg में) के निम्नलिखित आँकड़ों के लिए एक बारम्बारता बंटन सारणी बनाइए
40, 38, 33, 48, 60, 53, 31, 46, 34, 36, 49, 41, 55, 49, 65, 42, 44, 47, 38, 39
हल:
बारम्बारता बंटन निम्न प्रकार से बनाएंगे-

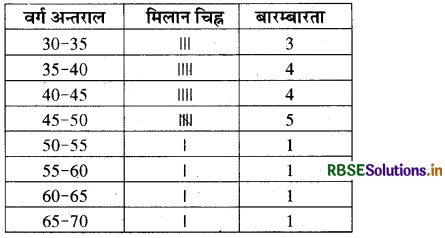
(प्रयास कीजिए - पृष्ठ 80)

प्रश्न 1.
आयत चित्र (आकृति) को देखिए और उसके नीचे दिए गए प्रश्नों के उत्तर दीजिए-

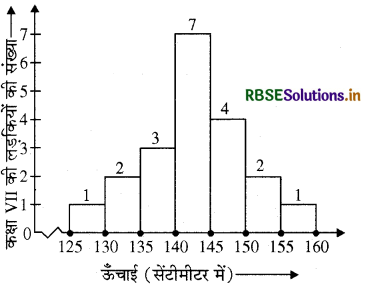
(i) इस आयत चित्र के द्वारा क्या सूचना दी जा रही है?
हल:
इस आयत चित्र के द्वारा कक्षा VII की लड़कियों की ऊँचाई (cm में) के बारे में सूचना दी जा रही है।

(ii) किस वर्ग में अधिकतम लड़कियाँ हैं?
हल:
140-145 वर्ग में अधिकतम लड़कियाँ हैं।

(iii) कितनी लड़कियों की लम्बाई 145 cm या उससे अधिक है?
हल:
7 लड़कियों की लम्बाई 145 cms या उससे अधिक है।

(iv) यदि हम लड़कियों को निम्नलिखित तीन श्रेणियों में विभाजित करें, तो प्रत्येक में कितनी लड़कियाँ होंगी?
150 cm या उससे अधिक 140 cm या - समूह A
उससे अधिक परन्तु 150 cm से कम - समूह B
140 cm से कम - समूह c
हल:
समूह A में 2 + 1 = 3 लड़कियाँ ।
समूह B में 7 + 4 = 11 लड़कियाँ।
समूह C में 1 + 2 + 3 = 6 लड़कियाँ।

(प्रयास कीजिए - पृष्ठ 83)

प्रश्न 1.
निम्नलिखित पाई चार्टों में से प्रत्येक (आकृति) आपकी कक्षा के बारे में एक भिन्न प्रकार की सूचना देता है। इनमें से प्रत्येक सूचना को निरूपित करने वाले वृत्त का भाग ज्ञात कीजिए।
(i)

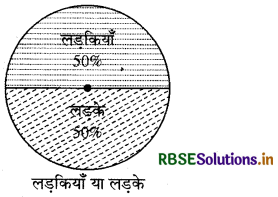
हल:

(ii)

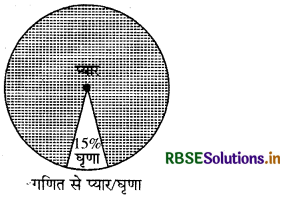
हल:
दिये गये पाई चार्ट से स्पष्ट है

(iii)

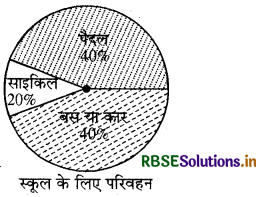
हल:
दिये गये पाई चार्ट से स्पष्ट है

प्रश्न 2.
दिए हुए पाई चार्ट (आकृति) के आधार पर निम्नलिखित प्रश्नों के उत्तर दीजिए
(i) किस प्रकार के कार्यक्रम सबसे अधिक देखे जाते हैं?
(ii) किन दो प्रकार के कार्यक्रमों को देखने वालों की कुल संख्या खेलों के कार्यक्रमों को देखने वालों की संख्या के बराबर है?

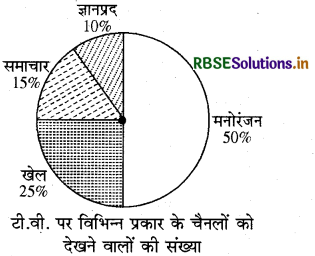
हल:
दिए गए पाई चार्ट से स्पष्ट है|
(i) मनोरंजन कार्यक्रम सबसे अधिक देखे जाते हैं।
(ii) समाचार और ज्ञानप्रद कार्यक्रमों को देखने वालों की कुल संख्या खेलों के कार्यक्रमों को देखने वालों की संख्या के बराबर है।

(प्रयास कीजिए - पृष्ठ 85)

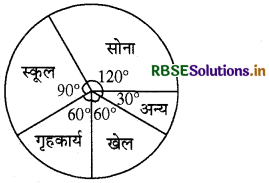
प्रश्न-नीचे दिए गए आंकड़ों के लिए एक पाई चार्ट खींचिए है-
एक बच्चे द्वारा एक दिन में व्यतीत किया गया समय इस प्रकार है-
सोना- 8 घण्टे
स्कूल- 6 घण्टे
गृहकार्य - 4 घण्टे
खेल - 4 घण्टे
अन्य - 2 घण्टे
हल:
इन आँकड़ों को पाई चार्ट में दर्शाते हैं । केन्द्र पर कुल कोण 360° तथा त्रिज्य खण्ड कोण 360 के भाग होंगे।

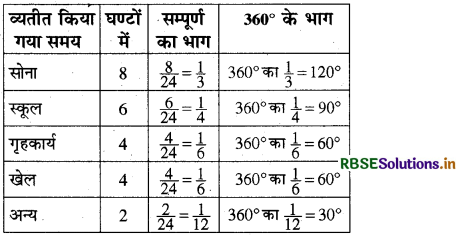
हम नीचे दर्शारा अनुसार पाई चार्ट बनाएँगे 

(सोचिए, चर्चा कीजिए और लिखिए - पृष्ठ 86)

निम्नलिखित आँकड़ों को दर्शाने के लिए, किस प्रकार का आलेख उपयुक्त रहेगा?

प्रश्न 1.
किसी राज्य के खाद्यान्न का उत्पादन

हल:
इन आँकड़ों के लिए दण्ड आलेख उपयुक्त रहेगा।

प्रश्न 2.
व्यक्तियों के एक समूह के भोजन की पसन्द-

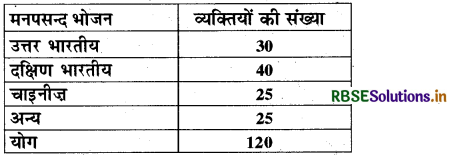
हल:
इन आँकड़ों के लिए वृत्त आलेख या पाई चार्ट उपयुक्त रहेगा।

प्रश्न 3.
किसी फैक्ट्री के श्रमिकों के एक समूह की दैनिक आय

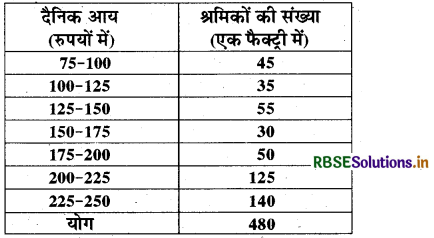
हल:
इन आँकड़ों को दर्शाने के लिए आयत चित्र उपयुक्त रहेगा।

(प्रयास कीजिए - पृष्ठ 88-89)

प्रश्न 1.
यदि आप एक स्कूटर चलाना प्रारम्भ करें, तो संभव परिणाम क्या हैं?
हल:
स्कूटर चलाने के संभावित परिणाम होंगे कि स्कूटर चल जाएगा अथवा नहीं चलेगा।

प्रश्न 2.
जब एक पासे (die) को फेंका जाता है, तो संभव छह परिणाम क्या हैं?
हल:
एक पासे को फेंकने पर संभावित परिणाम के रूप में 1, 2, 3, 4, 5, 6 अंकित कोई एक अंक पासे की ऊपर की सतह पर आएगा।

प्रश्न 3.
जब आप पहिए को घुमाएंगे, तो संभावित परिणाम क्या होंगे (आकृति)? इनकी सूची बनाइए।

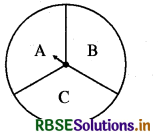
[यहाँ परिणाम का अर्थ है कि वह त्रिज्य खण्ड जहाँ पर सूचक (Pointer) घुमाने पर रुकेगा।
हल:
पहिए को घुमाने के निम्नलिखित संभावित परिणाम हो सकते हैं
(i) पहिया A त्रिज्य खण्ड पर रुके।
(ii) पहिया B त्रिज्य खण्ड पर रुके।
(iii) पहिया C त्रिज्य खण्ड पर रुके।

प्रश्न 4.
आपके पास एक थैला है और उसमें भिन्न-भिन्न रंगों की पाँच एक जैसी गेंदे हैं (आकृति)। आप बिना देखे इसमें से एक गेंद निकालते हैं। प्राप्त होने वाले परिणामों को लिखिए।

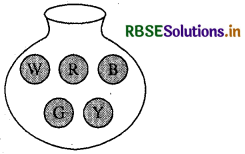
हल:
एक थैला जिसमें 1 सफेद, 1 लाल, 1 नीली, 1 हरी और 1 पीली गेंद, हैं। निकलने वाली गेंद w, R, B, G अथवा Y में से कोई एक होगी।

(सोचिए, चर्चा कीजिए और लिखिए - पृष्ठ 89)

प्रश्न-एक पासे को फेंकने पर]

• क्या पहले खिलाड़ी के 6 प्राप्त करने का संयोग अधिक
• क्या उसके बाद खेलने वाले खिलाड़ी के 6 प्राप्त करने का संयोग कम है?
• मान लीजिए कि दूसरा खिलाड़ी 6 प्राप्त कर लेता है। क्या इसका अर्थ यह है कि तीसरे खिलाड़ी द्वारा 6 प्राप्त करने का कोई संयोग नहीं है?

हल:
जब हम पासे को कई बार फेंकते हैं, तो प्रत्येक बार 1 अथवा 2 अथवा 3 अथवा 4 अथवा 5 अथवा 6 में से 6 प्राप्त करने की संभावना समान रहती है अर्थात् यह दर्शाता है कि प्रत्येक परिणाम की संभावना समान है। अतः सभी खिलाड़ियों के लिए सभी दशाओं में 6 प्राप्त करने का संयोग समान है।

(प्रयास कीजिए - पृष्ठ 91)

प्रश्न-मान लीजिए कि आप पहिए को घुमाते हैं (आकृति)।
(i) इस पहिए पर एक हरा त्रिज्य खण्ड प्राप्त करने के परिणामों की संख्या और हरा त्रिज्य खण्ड प्राप्त न होने के परिणामों की संख्या लिखिए।
(ii) एक हरा त्रिज्य खण्ड प्राप्त करने की प्रायिकता ज्ञात कीजिए।
(iii) एक हरा त्रिज्य खण्ड प्राप्त न होने की प्रायिकता ज्ञात कीजिए।

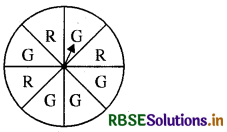
हल:
(i) एक हरा त्रिज्य खण्ड प्राप्त करने के परिणामों की संख्या = 5
और एक हरा त्रिज्य खण्ड प्राप्त नहीं करने की संभावना
(ii) एकं हरा त्रिज्य खण्ड प्राप्त करने की प्रायिकता

= \(\frac{5}{8}\)

(iii) एक हरा त्रिज्य खण्ड प्राप्त नहीं होने की प्रायिकता = \(\frac{3}{8}\)