RBSE Solutions for Class 8 Maths Chapter 3 चतुर्भुजों को समझना Ex 3.4

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 3 चतुर्भुजों को समझना Ex 3.4 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 3 चतुर्भुजों को समझना Ex 3.4

प्रश्न 1.
बताइए कथन सत्य है या असत्य
(a) सभी आयत वर्ग होते हैं।
हल:
असत्य

(b) सभी सम चतुर्भुज समान्तर चतुर्भुज होते हैं।
हल:
सत्य

(c) सभी वर्ग सम चतुर्भुज और आयत भी होते हैं।
हल:
सत्य

(d) सभी वर्ग समातंर चतुर्भुज नहीं होते।
हल:
असत्य

(e) सभी पतंगें सम चतुर्भुज होती हैं।
हल:
असत्य

(f) सभी सम चतुर्भुज पतंग होते हैं।
हल:
सत्य

(g) सभी समांतर चतुर्भुज समलंब होते हैं।
हल:
सत्य

(h) सभी वर्ग समलंब होते हैं।
हल:
सत्य

प्रश्न 2.
उन सभी चतुर्भुजों की पहचान कीजिए जिनमें
(a) चारों भुजाएँ बराबर लम्बाई की हों
हल:
वह चतुर्भुज जिसकी चारों भुजाओं की लम्बाई बराबर है या तो वर्ग है या समचतुर्भुज है।

(b) चार समकोण हों।
हल:
वह चतुर्भुज जिसके चारों कोण समकोण हैं या तो वर्ग है या आयत है।

प्रश्न 3.
बताइए कैसे एक वर्ग
(i) एक चतुर्भुज
हल:
एक वर्ग की चार भुजाएँ होती हैं। अत: यह एक चतुर्भुज है।

(ii) एक समांतर चतुर्भुज
हल:
एक वर्ग की सम्मुख भुजाओं का युग्म समांतर होता है, अतः यह एक समांतर चतुर्भुज है।

(iii) एक समचतुर्भुज
हल:
एक वर्ग एक समांतर चतुर्भुज है जिसकी चारों भुजाएँ बराबर लम्बाई की होती हैं, अतः यह एक सम चतुर्भुज है।

(iv) एक आयत है?
हल:
एक वर्ग एक समांतर चतुर्भुज है जिसका प्रत्येक कोण समकोण है, अतः यह एक आयत है।

प्रश्न 4.
एक चतुर्भुज का नाम बताइए जिसके विकर्ण
(i) एक-दूसरे को समद्विभाजित करते हैं।
हल:
एक चतुर्भुज जिसके विकर्ण एक-दूसरे को समद्विभाजित करते हैं, वह या तो समांतर चतुर्भुज या सम चतुर्भुज, या वर्ग या आयत हो सकता है।

(ii) एक-दूसरे पर लम्ब समद्विभाजक हों।
हल:
एक चतुर्भुज जिसके विकर्ण एक-दूसरे पर लम्ब समद्विभाजक हों या तो सम चतुर्भुज है या वर्ग है।

(iii) बराबर हों।
हल:
एकं चतुर्भुज जिसके विकर्ण बराबर हैं वह या तो वर्ग, या आयत हो सकता है।

प्रश्न 5.
बताइए एक आयत उत्तल चतुर्भुज कैसे है?
हल:
चूंकि एक आयत के प्रत्येक कोण का माप 180° से कम होता है तथा साथ ही आयत के दोनों विकर्ण पूरी तरह अन्दर (अभ्यंतर) होते हैं। अतः एक आयत एक उत्तल चतुर्भुज है।

प्रश्न 6.
ABC एक समकोण त्रिभुज है और '0' समकोण की सम्मुख भुजा का मध्य बिन्दु है। बताइए कैसे '0' बिन्दु A, B तथा C से समान दूरी पर स्थित है। (बिन्दुओं से चिह्नित अतिरिक्त भुजाएँ आपकी सहायता के लिए खींची गई हैं।)

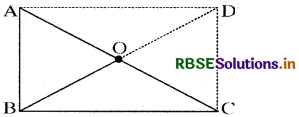
हल:
BO को D तक इस प्रकार बढ़ाइए कि कि BO = OD है। AD और DC को मिलाइए। इस प्रकार प्राप्त ABCD एक आयत है। इस आयत ABCD में, इसके विकर्ण AC तथा BD बराबर हैं तथा एक-दूसरे को o बिन्दु पर काटते हैं।
अतः OA = OC तथा OB = OD
परन्तु AC = BD
इसलिए OA = OB = OC
अतः O बिन्दु A, B तथा C से बराबर दूरी पर है।