RBSE Solutions for Class 7 Maths Chapter 5 रेखा एवं कोण Ex 5.2

Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 5 रेखा एवं कोण Ex 5.2 Textbook Exercise Questions and Answers.

RBSE Class 7 Maths Solutions Chapter 5 रेखा एवं कोण Ex 5.2

प्रश्न 1.
निम्नलिखित कथनों में प्रत्येक कथन में उपयोग किए गए गुणधर्म का वर्णन कीजिए (देखें आकृति)।

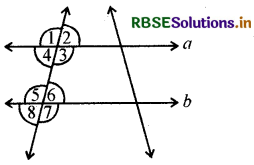
(i) यदि a || b, तो ∠1 = ∠5
हल:
संगत कोण गुण।।

(ii) यदि ∠4 = ∠6, तो a|| b
हल:
एकान्तर कोण गुण का प्रतिलोम।

(iii) यदि ∠4 + ∠5 = 180°, तो a||b
हल:
तिर्यक रेखा के एक ही ओर के अन्त:कोण सम्पूरक होते हैं का प्रतिलोम।

प्रश्न 2.
आकृति में निम्नलिखित की पहचान कीजिए :

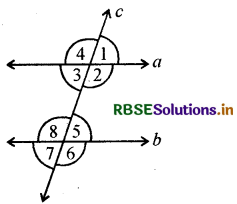
(i) संगत कोणों के युग्म
हल:
∠1, ∠5, ∠2, ∠6; ∠3, ∠7 और ∠4, ∠8 चार संगत कोणों के युग्म हैं।

(ii) अन्तः एकान्तर कोणों के युग्म
हल:
एकान्तर कोणों के दो युग्म हैं- ∠2, ∠8 और ∠3, ∠5

(iii) तिर्यक छेदी रेखा के एक तरफ बने अन्तःकोणों के युग्म
हल:
तिर्यक रेखा के एक ही ओर के अन्त:कोणों के दो युग्म हैं- ∠2, ∠5 और ∠3, ∠8

(iv) शीर्षाभिमुख कोण।
हल:
शीर्षाभिमुख कोणों के चार युग्म हैं- ∠1, ∠3; ∠2, ∠4; ∠5, ∠7 और ∠6, ∠8

प्रश्न 3.
संलग्न आकृति में p || q। अज्ञात कोण ज्ञात कीजिए।

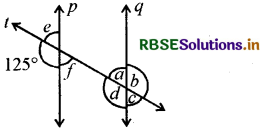
हल:
यहाँ, ∠e + 125° = 180° [रैखिक युग्म]
इसलिए ∠e = 180° - 125° = 550
∠f = ∠e = 55° [ऊर्ध्वाधर सम्मुख कोण]
क्योंकि p || q और t तिर्यक रेखा है, इसलिए
∠a = ∠f [एकान्तर कोण]
= 55° [∵ ∠f = 55°]
∠d = 125° [संगत कोण]
∠c = ∠a = 55°
[ऊर्ध्वाधर सम्मुख कोण]
और ∠b = ∠d = 125°
[ऊर्ध्वाधर सम्मुख कोण]
अतः, ∠a = 55°, ∠b = 125°, ∠c = 55°, ∠d = 125°, ∠e = 55° और ∠f = 55°

प्रश्न 4.
यदि l ||m है, तो निम्नलिखित आकृतियों में प्रत्येक में x का मान ज्ञात कीजिए:
(i)

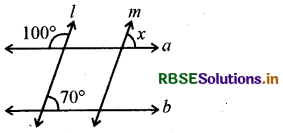
हल:
(i) क्योंकि l || m और a तिर्यक छेदी रेखा है, इसलिए
∠x = (180° - 110) [संगत कोण, रैखिक युग्म]
= 70°

(ii)

हल:
यदि l || m और a एक तिर्यक छेदी रेखा है, तब
∠x = 100° [संगत कोण]

प्रश्न 5.
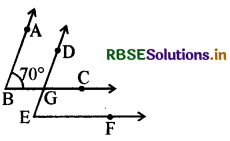
सामने दी हुई आकृति में, दो कोणों की । भुजाएँ समान्तर हैं। यदि ∠ABC = 70°, तो
(i) ∠DGC ज्ञात कीजिए।
हल:
क्योंकि AB || ED और BC तिर्यक छेदी रेखा है,
इसलिए ∠DGC = ∠ABC [संगत कोण]
= 70°
[∵ ∠ABC = 70°, दिया है]

(ii) ∠DEF ज्ञात कीजिए।
हल:
क्योंकि BC || EF और ED तिर्यक छेदी रेखा है, इसलिए
∠DEF = ∠DGC = 70° [संगत कोण]

प्रश्न 6.
नीचे दी हुई आकृतियों में निर्णय लीजिए कि क्या l, m के समान्तर है?
(i)

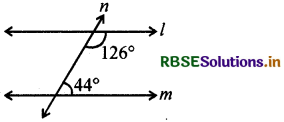
हल:
क्योंकि तिर्यक रेखा के एक ही ओर के अन्त:कोण सम्पूरक नहीं हैं।
(126° + 44° = 170° ≠ 180°)
∴ l, m के समान्तर नहीं है।

(ii)

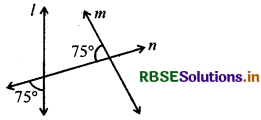
हल:
क्योंकि तिर्यक रेखा के एक ही ओर के अन्त:कोणों का योग 180° नहीं है, इसलिए,
l, m के समान्तर नहीं है।

(iii)

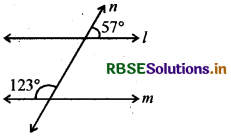
हल:
क्योंकि संगत कोण समान हैं।
[57° = (180° - 123°), अर्थात् 57°], इसलिए l, m के समान्तर है।

(iv)

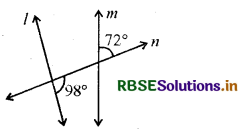
हल:
क्योंकि तिर्यक रेखा के एक ही ओर के अन्त:कोणों का योग 180° नहीं है। [∵ 98° + 72° = 170°]
∴ l, m के समान्तर नहीं है।