RBSE Solutions for Class 7 Maths Chapter 4 Simple Equations Intext Questions

Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 4 Simple Equations Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 7 Maths Solutions Chapter 4 Simple Equations Intext Questions

(Try These Page No: 78)

Question 1.
The value of the expression (10y - 20) depends on the value of y. Verify this by giving five different values to y and finding for each y the value of (10y - 20). From the different values of (10y - 20) you obtain, do you see a solution of 10y - 20 = 50? If there is no solution, try giving more values toy and find whether the condition 10y - 20 = 50 is met.
Answer:

The expression 10y - 20 ≠ 50 for above five values.

When we take y = 7, the condition 10y - 20 = 50 is met.

(Try These Page No: 88)

Question 1.
Start with the same step x = 5 and make two different equations. Ask two of your classmates to solve the equations. Check whether they get the solution x = 5.
Answer:
(i) x = 5
Multiply both sides by 2,
2x = 10
Subtract 3 from both sides,
2x - 3 = 10 - 3
or 2x- 3 = 7

(ii) x = 5
Divide both sides by 4,
\(\frac{x}{4}\) = \(\frac{5}{4}\)
Add 5 to both sides,

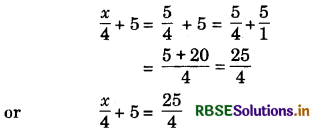
(Try These Page No: 88)

Question 1.
Try to make two number puzzles, one with the solution 11 and another with 100.
Answer:
1. With the solution 11.
(i) Think of a number, multiply it by 2 and add 8. If the sum is 30, then the number is 11.
(ii) Think of a number, multiply it by 5 and
subtract 11. If the difference is 44, then number is 11. [Hint: 5x - 11 = 44]

2. With the solution 100.
(i) Think of a number, divide it by 10 and add 8. If you get 18, then the number is 100.
(ii) Think of a number, divide it by 25 and add 5. If you get 9, then the number is 100.

(Try These Page No: 90)

Question 1.
(i) When you multiply a number by 6 and subtract 5 from the product, you get 7. Can you tell what the number is? (ii) What is that number one third of which added to 5 gives 8?
Answer:
(i) Let the required number be x.
According to question,
6x - 5 = 7
Transpose - 5 from L.H.S. to R.H.S.,
6x = 5 + 7
⇒ 6x = 12
Divide both sides by 6,
\(\frac{6 x}{6}=\frac{12}{6}\)
⇒ x = 2
∴ The required number is 2.

(ii) Let the number be x.
According to question,
x × \(\frac{1}{3}\) + 5 = 8
= \(\frac{x}{3}\) + 5 = 8
Transpose 5 from L.H.S. to R.H.S.,
\(\frac{x}{3}\) = 8 - 5
⇒ \(\frac{x}{3}\) = 3
Multiply both sides by 3,
3 × \(\frac{x}{3}\) = 3 × 3
⇒ x = 9
∴ The required number is 9.

Question 2.
There are two types of boxes containing mangoes. Each box of the larger type contains 4 more mangoes than the number of mangoes contained in 8 boxes of the smaller type. Each larger box contains 100 mangoes. Find the number of mangoes contained in the smaller box?
Answer:
Let x be the number of mangoes contained in the smaller box.
According to question,
4 + 8x =100
Transpose 4 from L.H.S. to R.H.S.,
8x = 100 - 4
⇒ 8x = 96
Divide both sides by 8,
\(\frac{8 x}{8}=\frac{96}{8}\)
⇒ x = 12
∴ The number of mangoes contained in the Smaller box is 12.