RBSE Solutions for Class 12 Maths Chapter 7 समाकलन विविध प्रश्नावली

Rajasthan Board RBSE Solutions for Class 12 Maths Chapter 7 समाकलन विविध प्रश्नावली Textbook Exercise Questions and Answers.

RBSE Class 12 Maths Solutions Chapter 7 समाकलन विविध प्रश्नावली

7 पर वि 1 से 24 तक के प्रश्नों के फलनों का समाकलन कीजिए

प्रश्न 1.
\(\frac{1}{x-x^3}\)
हल:
माना कि
I = \(\frac{1}{x-x^3}=\frac{1}{x\left(1-x^2\right)}=\frac{1}{x(1+x)(1-x)}\)
= \(\frac{\mathrm{A}}{x}+\frac{\mathrm{B}}{1+x}+\frac{\mathrm{C}}{1-x}\)
∴ 1 = A(1 - x²) + Bx(1 - x) + Cx(1 + x) .... (1)
(1) में x = 0 रखने पर
1 = A ∴ A = 1
(1) में x = - 1 रखने पर
1 = B (- 1) (1 + 1) = - 2B ∴ B = - \(\frac{1}{2}\)
(1) में x = 1 रखने पर
1 = C . 1 . (1 + 1) = 2C ∴ C = \(\frac{1}{2}\)

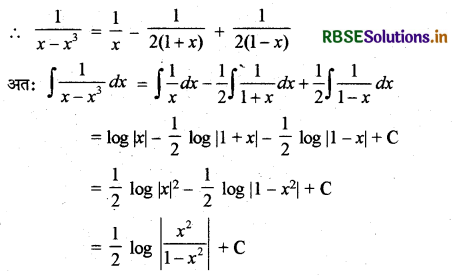
प्रश्न 2.
\(\frac{1}{\sqrt{x+a}+\sqrt{x+b}}\)
हल:
माना कि

प्रश्न 3.
\(\frac{1}{x \sqrt{a x-x^2}}\) (संकेत : x = \(\frac{a}{t}\) रखिए)
हल:

प्रश्न 4.
\(\frac{1}{x^2\left(x^4+1\right)^{3 / 4}}\)
हल:
माना कि

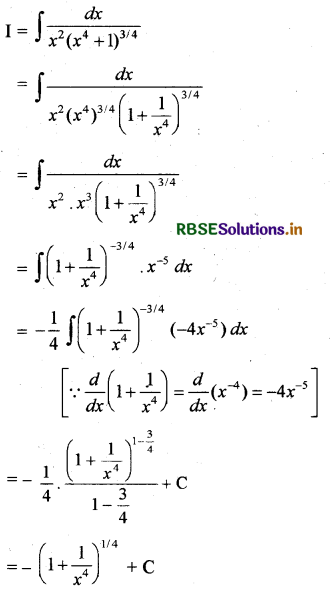
प्रश्न 5.

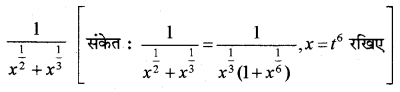
हल:
माना कि

प्रश्न 6.
\(\frac{5 x}{(x+1)\left(x^2+9\right)}\)
हल:
माना कि
\(\frac{5 x}{(x+1)\left(x^2+9\right)}=\frac{\mathrm{A}}{x+1}+\frac{\mathrm{B} x+\mathrm{C}}{x^2+9}\)
∴ 5x = A(x² + 9) + (Bx + C) (x + 1)
= A(x² + 9) + B(x² + x) + C(x + 1)
x = - 1 रखने पर
- 5 = A 10 ∴ A = - \(\frac{1}{2}\)
x² के गुणांकों की तुलना करने पर
0 = A + B ∴ B = \(\frac{1}{2}\)
अचर राशि की तुलना करने पर
0 = 9A + C ∴ C = - 9A = \(\frac{9}{2}\)

प्रश्न 7.
\(\frac{\sin x}{\sin (x-a)}\)
हल:
माना कि

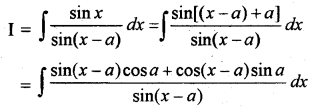
= ∫[cos a + cot(x - a)sin a] dx
= x cos a + sin a log |sin (x - a)| + C
I = sin a log |sin (x - a)| + x cos a + C

प्रश्न 8.
\(\frac{e^{5 \log x}-e^{4 \log x}}{e^{3 \log x}-e^{2 \log x}}\)
हल:
माना कि

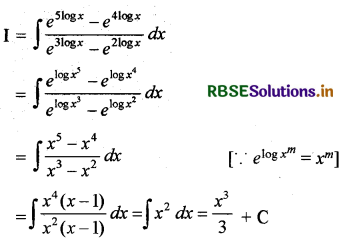
प्रश्न 9.
\(\frac{\cos x}{\sqrt{4-\sin ^2 x}}\)
हल:
माना कि

प्रश्न 10.
\(\frac{\sin ^8 x-\cos ^8 x}{1-2 \sin ^2 x \cos ^2 x}\)
हल:
माना कि I = ∫\(\frac{\sin ^8 x-\cos ^8 x}{1-2 \sin ^2 x \cos ^2 x}\) dx
अब
यहाँ sin x = 1 रखने पर cos x dx = dt .
अब sin⁸ x - cos⁸ x
= (sin⁴ x - cos⁴ x) (sin⁴ x + cos⁴ x)
= (sin² x + cos² x) (sin² x - cos² x)
(sin⁴ x + cos⁴ x)
= (sin² x - cos² x) {(sin² x + cos² x)² - 2 sin² x cos² x}
[∵ a² + b² = (a + b)² - 2ab]
= (sin² - cos² x) [1 - 2 sin² x cos² x]

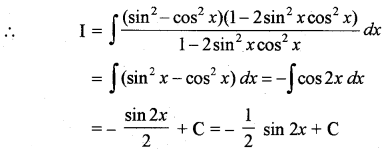
प्रश्न 11.
\(\frac{1}{\cos (x+a) \cos (x+b)}\)
हल:
माना कि

प्रश्न 12.
\(\frac{x^3}{\sqrt{1-x^8}} \)
हल:
माना कि

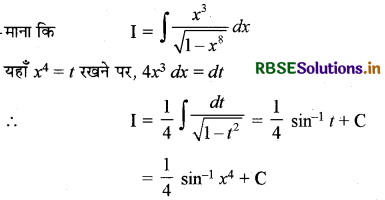
प्रश्न 13.
\(\frac{e^x}{\left(1+e^x\right)\left(2+e^x\right)}\)
हल:
माना कि
I = ∫\(\frac{e^x}{\left(1+e^x\right)\left(2+e^x\right)}\) dx
यहाँ e^x = t रखने पर, e^x dx = dt
∴ I = ∫\(\frac{d t}{(1+t)(2+t)}\)
अब \(\frac{1}{(1+t)(2+t)}=\frac{\mathrm{A}}{1+t}+\frac{\mathrm{B}}{2+t}\)
∴ 1 = A(2 + 1) + B(1 + t)
अब t = - 1 रखने पर 1 = A . 1 ∴ A = 1
तथा t = - 2 रखने पर 1 = B(1 - 2) ∴ B = - 1

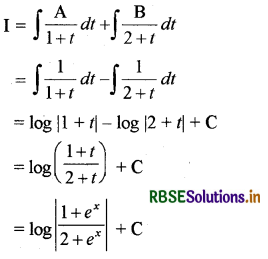
प्रश्न 14.
\(\frac{1}{\left(x^2+1\right)\left(x^2+4\right)}\)
हल:
माना कि
I = ∫\(\frac{1}{\left(x^2+1\right)\left(x^2+4\right)}\)
x² = y रखने पर,
\(\frac{1}{\left(x^2+1\right)\left(x^2+4\right)}=\frac{1}{(y+1)(y+4)}=\frac{\mathrm{A}}{y+1}+\frac{\mathrm{B}}{y+4}\)
अब y = - 1 रखने पर
1 = A(- 1 + 4) = 3A ∴ A = \(\frac{1}{3}\)
तथा y = - 4 रखने पर
1 = B(- 4 + 1) = - 3B ∴ B = - \(\frac{1}{3}\)
अर्थात्

प्रश्न 15.
cos³ x e^{log sin x}
हल:
माना कि I = ∫cos³ x e^{log sin x} dx = ∫cos³ x sin x dx
अब cos x = t रखने पर, - sin x dx = dt [∵ e^{log x} = x]
∴ I = ∫t³ (- dt) = - ∫t³ dt = - \(\frac{t^4}{4}\) + C
= - \(\frac{\cos ^4 x}{4}\) + C = - \(\frac{1}{4}\) cos⁴ x + C

प्रश्न 16.
e^{3 log x} (x⁴ + 1)^-1
हल:
माना कि
I = ∫e^{3 log x} (x⁴ + 1)^-1 dx

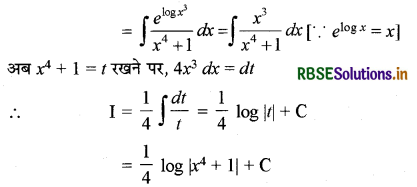
प्रश्न 17.
f'(ax + b) [f(ax + b)]ⁿ
हल:
माना कि
I = ∫[f(ax + b)]ⁿ f'(ax + b) dx
अब f(ax + b) = t रखने पर ∴ f'(ax + b).a dx = dt
∴ I = ∫\(t^n \cdot \frac{1}{a} d t=\frac{1}{a} \cdot \frac{t^{n+1}}{n+1}+\mathrm{C}\)
I = \(\frac{[f(a x+b)]^{n+1}}{a(n+1)}\) + C

प्रश्न 18.
\(\frac{1}{\sqrt{\sin ^3 x \sin (x+\alpha)}}\)
हल:
माना कि I = ∫\(\frac{1}{\sqrt{\sin ^3 x \sin (x+\alpha)}}\) dx
अब
sin³ x sin x (x + α) = sin³ x (sin x cos α + cos x sin α)
= sin⁴ x (cos α + cot x sin α)

प्रश्न 19.
\(\frac{\sin ^{-1} \sqrt{x}-\cos ^{-1} \sqrt{x}}{\sin ^{-1} \sqrt{x}+\cos ^{-1} \sqrt{x}}\), (x ∈ [0, 1])
हल:
माना कि

ILATE के अनुसार, sin^-1 t को पहला फलन मानकर खण्डशः
समाकलन करने पर

प्रश्न 20.
\(\sqrt{\frac{1-\sqrt{x}}{1+\sqrt{x}}}\)
हल:
माना कि I = ∫\(\sqrt{\frac{1-\sqrt{x}}{1+\sqrt{x}}}\)
अब √x = cos t या x = cos² t रखने पर
∴ dx = - 2 cos t sin t dt

प्रश्न 21.
\(\frac{2+\sin 2 x}{1+\cos 2 x}\) e^x
हल:
माना कि

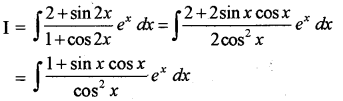
= ∫e^x (tan x + sec² x) dr
अब e^x tan x = 1 रखने पर
(e^x sec² x + e^x tan x) dx = dt ∴ e^x (tan x + sec² x) dx = dt
∴ I = ∫dt = t + C = e^x tan x + C

प्रश्न 22.
\(\frac{x^2+x+1}{(x+1)^2(x+2)}\)
हल:
माना कि
I = ∫\(\frac{x^2+x+1}{(x+1)^2(x+2)}\) dx
अब
\(\frac{x^2+x+1}{(x+2)(x+1)^2}=\frac{\mathrm{A}}{x+2}+\frac{\mathrm{B}}{x+1}+\frac{\mathrm{C}}{(x+1)^2}\)
∴ x² + x + 1 = A(x + 1)² + B(x + 2) (x + 1) + C(x + 2)
= A(x² + 2x + 1) + B(x² + 3x + 2) + C(x + 2)
यहाँ x = - 2 रखने पर,
4 - 2 + 1 = A(- 1)² या 3 = A ∴ A = 3
तथा x = - 1 रखने पर,
1 - 1 + 1 = C(- 1 + 2) = C ∴ C = 1
x² के गुणांकों की तुलना करने पर
1 = A + B ∴ B = 1 - A
= 1 - 3 = - 2

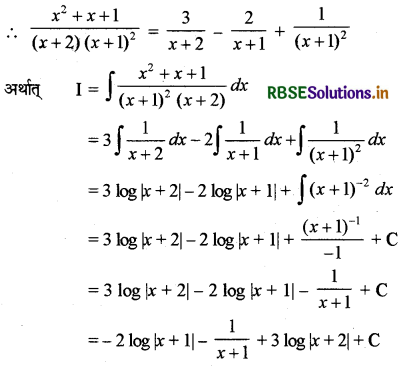
प्रश्न 23.
tan^-1\(\sqrt{\frac{1-x}{1+x}}\)
हल:
माना कि I = ∫tan^-1\(\sqrt{\frac{1-x}{1+x}}\) dx
अब x = cos θ रखने पर dx = - sin θ dθ

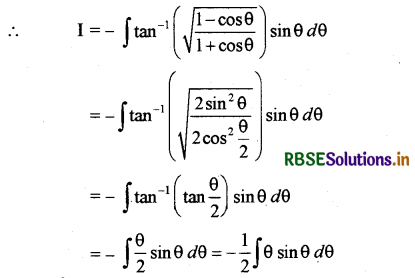
ILATE के अनुसार, को पहला फलन मानकर खण्डशः समाकलन करने पर

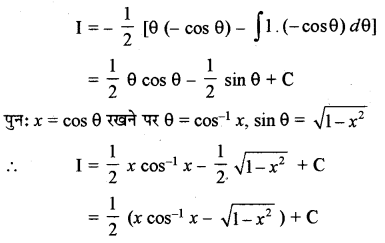
प्रश्न 24.
\(\frac{\sqrt{x^2+1}\left[\log \left(x^2+1\right)-2 \log x\right]}{x^4}\)
हल:
माना कि

25 से 33 तक के प्रश्नों में निश्चित समाकलनों का मान ज्ञात कीजिए।

प्रश्न 25.
\(\int_{\frac{\pi}{2}}^\pi e^x\left(\frac{1-\sin x}{1-\cos x}\right)\) dx
हल:
माना कि

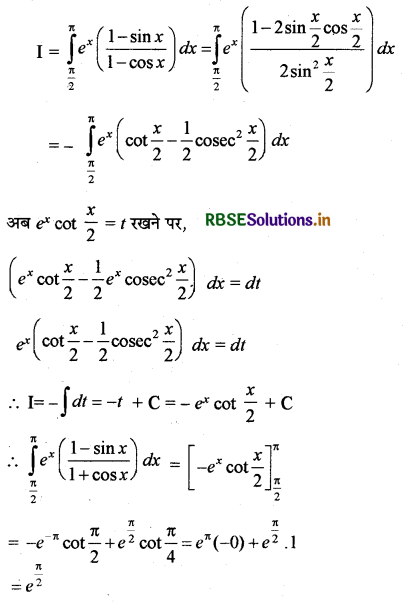
प्रश्न 26.
\(\int_0^{\frac{\pi}{4}} \frac{\sin x \cos x}{\cos ^4 x+\sin ^4 x}\) dx
हल:
माना कि

प्रश्न 27.
\(\int_0^{\frac{\pi}{2}} \frac{\cos ^2 x d x}{\cos ^2 x+4 \sin ^2 x}\)
हल:
माना कि

प्रश्न 28.
\(\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \frac{\sin x+\cos x}{\sqrt{\sin 2 x}}\) dx
हल:
माना कि

प्रश्न 29.
\(\int_0^1 \frac{d x}{\sqrt{1+x}-\sqrt{x}} \)
हल:
माना कि

प्रश्न 30.
\(\int_0^{\frac{\pi}{4}} \frac{\sin x+\cos x}{9+16 \sin 2 x}\) dx
हल:
माना कि
I = \(\int_0^{\frac{\pi}{4}} \frac{\sin x+\cos x}{9+16 \sin 2 x}\) dx
यहाँ sin x - cos x = t रखने पर (cos x + sin x) dx = dt
अतः यदि x = \(\frac{\pi}{4}\) तो t = 0 तथा यदि x = 0 तो t = - 1
(sin x - cos x)² = 1 - 2 sin x cos x = 1 - sin 2x
∴ sin 2x = 1 - (sin x - cos x)² = 1 - t²

प्रश्न 31.
\(\int_0^{\pi / 2}\) sin 2x tan^-1 (sin x) dx
हल:
माना कि
I = \(\int_0^{\pi / 2}\) sin 2x tan^-1 (sin x) dx
यहाँ sin x = t रखने पर, cos x dx = dt
अतः यदि x = \(\frac{\pi}{2}\) तो t = 1, तथा यदि x = 0 तो t = 0
∴ I = 2\(\int_0^1\) t tan^-1 t dt
ILATE के अनुसार, tan-11 को पहला फलन मानकर खण्डशः
समाकलन करने पर

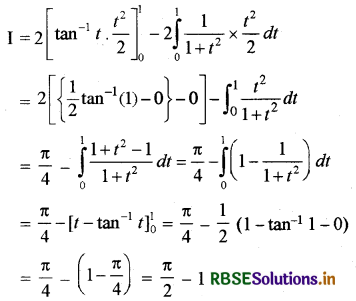
प्रश्न 32.
\(\int_0^\pi \frac{x \tan x}{\sec x+\tan x}\) dx
हल:
माना कि

प्रश्न 33.
\(\int_1^4\) (|x - 1| + |x - 2| + |x - 3|) dx
हल:
माना कि

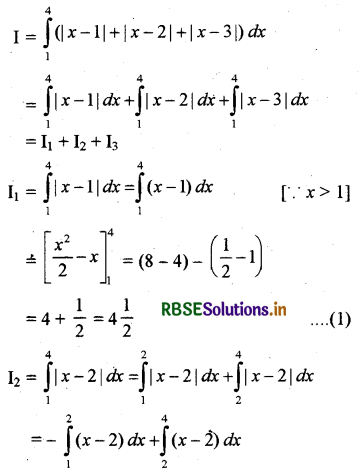
∵ यदि 1 < x < 2 तो |x - 2| = - (x - 2)
तथा यदि 2 < x < 4 तो |x - 2| = x - 2

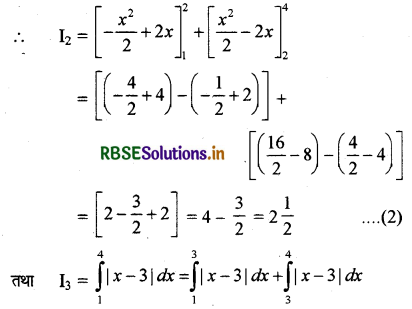
∵ यदि 1 < x < 2 तो |x - 3| = - (x - 3)
तथा यदि 3 < x < 4 तो |x - 3| = x - 3

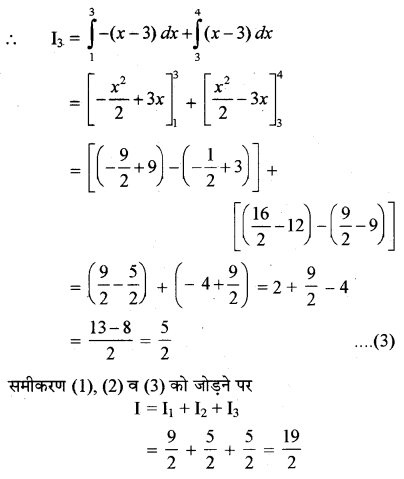
निम्नलिखित को सिद्ध कीजिए (प्रश्न 34 से 39 तक):

प्रश्न 34.
\(\int_1^3 \frac{d x}{x^2(x+1)}=\frac{2}{3}+\log \frac{2}{3}\)
हल:
माना कि I = \(\int_1^3 \frac{d x}{x^2(x+1)}\)
यहाँ \(\frac{1}{x^2(x+1)}=\frac{\mathrm{A}}{x}+\frac{\mathrm{B}}{x^2}+\frac{\mathrm{C}}{x+1}\)
∴ 1 = Ax(x + 1) + B(x + 1) + Cx²
x = 0 रखने पर 1 = B. 1 ∴ B = 1
x = - 1 रखने पर 1 = C . (- 1)² ∴ C = 1
x² के गुणांकों की तुलना करने पर
0 = A + C ∴ A = - C = - 1

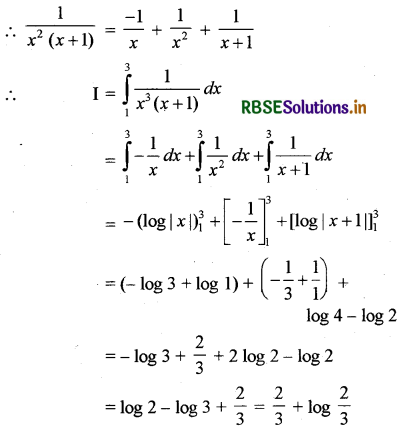
प्रश्न 35.
\(\int_0^1\) x e^x dx = 1
हल:
माना कि
I = \(\int_0^1\) x e^x dx
को पहला फलन मानकर खण्डशः समाकलन करने पर
I = \(\left[x . e^x\right]_0^1\) - \(\int_0^1\) 1.e^x dx
= 1.e¹ - \(\left[x . e^x\right]_0^1\) = e - (e - 1) = 1

प्रश्न 36.
\(\int_{-1}^1\) x¹⁷ cos⁴ x dx = 0
हल:
माना कि
I = \(\int_{-1}^1\) x¹⁷ cos⁴ x dx
f(x) = x¹⁷ cos⁴ x, f(- x) = (- x)¹⁷ cos⁴ x dx
= - (x¹⁷ cos⁴ x)
∴ f(- x) = - f(x), \(\int_{-a}^a\) f(x) dx = 0 यदि f विषम फलन हो
∴ I = 0 ⇒ \(\int_{-1}^1\) x¹⁷ cos⁴ x dx = 0

प्रश्न 37.
\(\int_\theta^{\pi / 2}\) sin³ dx = \(\frac{2}{3}\)
हल:
माना कि

प्रश्न 38.
\(\int_0^{\pi / 2}\) 2 tan³ x dx = 1 - log 2
हल:
माना कि

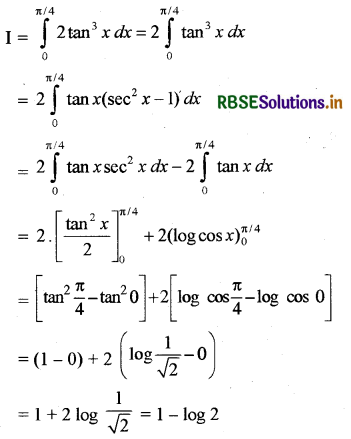
प्रश्न 39.
\(\int_0^1\) sin^-1 x dx = \(\frac{\pi}{2}\) - 1
हल:
माना कि
I = \(\int_0^1\) sin^-1 x . 1 dx
sin^-1 x को पहला फलन इकाई को द्वितीय फलन मानकर खण्डशः
समाकलन करने पर

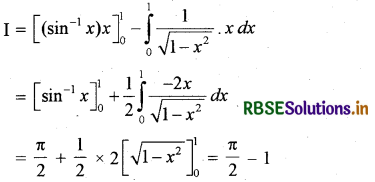
प्रश्न 40.
योगफल की सीमा के रूप में \(\int_0^1\) e^{2 - 3x} dx का मान ज्ञात कीजिए।
हल:
माना कि I = \(\int_0^1\) e^{2 - 3x} dx
हम जानते है कि

41 से 44 तक के प्रश्नों में सही उत्तर का चयन कीजिए:

प्रश्न 41.
∫\(\frac{d x}{e^x+e^{-x}}\) बराबर है:
(A) tan^-1 (e^x) + C
(B) tan^-1 (e^x) + C
(C) log (e^x - e^-x) + C
(D) log (e^x + e^-x) + C
उत्तरः
(A) tan^-1 (e^x) + C

हल:

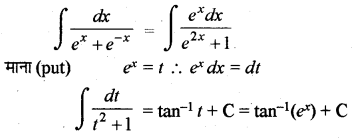
अतः सही विकल्प (A) है।

प्रश्न 42.
∫\(\frac{\cos 2 x}{(\sin x+\cos x)^2}\) बराबर है:
(A) \(\frac{-1}{\sin x+\cos x}\) + C
(B) log |sin x + cos x| + C
(C) log |sin x - cos x| + C
(D) \(\frac{1}{(\sin x+\cos x)^2}\)
उत्तरः
(B) log |sin x + cos x| + C

हल:

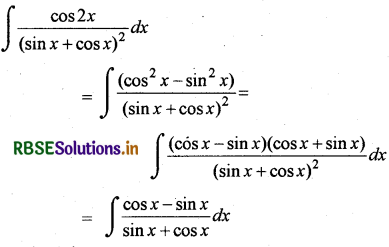
माना (put)sin x + cos x = t
(cos x - sin x)dx = dt
= ∫\(\frac{d t}{t}\) = log t + C
= log |sin x + cos x| + C
अतः सही विकल्प (B) है।

प्रश्न 43.
यादि f(a + b - x) = f(x), तो \(\int_a^b\) x f(x) dx बराबर है|
(A) \(\frac{a+b}{2} \int_a^b\) f(b-x) d x
(B) \(\frac{a+b}{2} \int_a^b\) f(b+x) d x
(C) \(\frac{b-a}{2} \int_a^b\) f(x)
(D) \(\frac{a+b}{2} \int_a^b\) f(x) d x
उत्तरः
(D) \(\frac{a+b}{2} \int_a^b\) f(x) d x

हल:
माना कि
I = \(\int_a^b\) x f(x) dx .......... (1)
गुणधर्म (P₄) के प्रयोग से

प्रश्न 44.
\(\int_0^1\) tan^-1\(\left(\frac{2 x-1}{1+x-x^2}\right)\) dx का मान है:
(A) 1
(B) 0
(C) - 1
(D) \(\frac{\pi}{4}\)
उत्तरः
(B) 0

हल:
माना कि

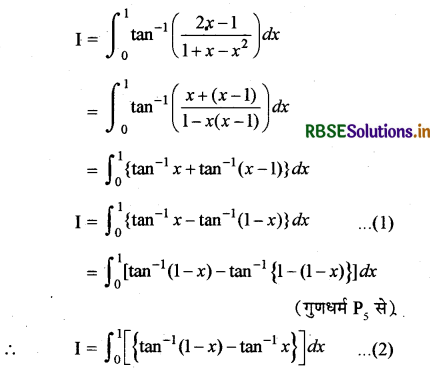
समी. (1) तथा (2) को जोड़ने पर
2I = 0 ⇒ I = 0
अतः सही विकल्प (B) है।