RBSE Solutions for Class 11 Maths Chapter 1 Sets Ex 1.1

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 1 Sets Ex 1.1 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 1 Sets Ex 1.1

Question 1.
Which of the following are sets? Justify your answer,
(i) The collection of all the months of a year beginning with the letter J.
Answer:
Since months of a year beginning with letter J are Januray, June and July.
These months are well defined. So, collection of all the month of a year beginning with letter J is a set.

(ii) The collection of ten most talented writers of India.
Answer:
There is no standard scale which defined talent of any writer. So, this collection is not a set.

(iii) A team of eleven best cricket batsman of the world.
Answer:
There is no standard scale to select best batsman of the world. So, this collection is not a set.

(iv) The collection of all boys in your class.
Answer:
Number ofboys in a class is finite. So, collection of all boys in a class is a set.

(v) The collection of all natural numbers less than 100.
Answer:
If all the natural numbers less than 100 are written in roster form then we get {1, 2, 3, 4, .... 99} which is defined, So, this collection represents a set.

(vi) A collection of novels wtitten by the writer Munshi Prem Chand.
Answer:
A collection of novels written by the writer Munshi Prem Chand is in finite number. So, it is well defined and represent a set.

(vii) The collection of all even integers.
Answer:
If all even integers are written in roster form, we get {2,4,6, 8,....}. It is not defined. So, not represents a set.

(viii) The collection of,questions in this chapter.
Answer:
A collection of questions in this chapter is finited. So, it represent a set.

(ix) A collection of most dangerous animals of the world.
Answer:
There is no scale to measure most dangerous animals in the world. So, it is not defined. So, not represents a set.

Question 2.
Let A = (1, 2, 3, 4, 5, 6}. Insert the appropriate symbol ∈ or ∉ in the blank spaces.
(i) 5 ............. A
Answer:
5 ∈ A
Since 5 occurs in A, thus 5 ∈ A.

(ii) 8 .............. A
Answer:
8 ∉ A
Since 8 not occur in A, thus 8 ∉ A.

(iii) 0 ............ A
Answer:
0 ∈ A
Since 0 not occur in A, thus 0 ∈ A.

(iv) 4 ..............A
Answer:
4 ∈ A
Since 4 occurs in A, thus 4 ∈ A.

(v) 2 ...............A
Answer:
2 ∈ A
Since 2 occurs in A, thus 2 ∈ A.

(vi) 10 ........... A
Solution:
10 ∉ A
∵ A = { 1,2,3, 4,5,6}
Thus, elements of set A are 1, 2, 3, 4, 5, and 6.
Since 10 not occurs in A, Thus 10 ∉ A

Question 3.
Write the followings sets in roster form :
(i) A = {x : x is an integer and -3 ≤ x ≤ 7}
(ii) B = {x : x is a natural number less than 6}
(iii) C= (x: x is a two-digit natural number such that the sum of its digits is 8}
(iv) D - (x : x is a prime number which is divisor of 60}
(v) E = The set of all letters in the word TRIGONOMETRY.
(vi) F = The set of all letters in the word BETTER.
Answer:
Roster form of given sets are as follows :
(i) A = {-3, -2, -1,0,1,2,3,4,5,6}
(ii) B = {1,2,3,4,5}
(iii) C = {17, 26, 35, 44, 53, 62, 71, 80}, here sum of digits of all numbers is 8.
(iv) D = {2, 3, 5}, here 2, 3 and 5 are prime numbers which are divisor of 60.
(v) E = { T, R, I, G. O, N, M,E, Y}, here letters are not repeated.
(vi) F= {B, E, T, R}, here letters are not repeated.

Question 4.
Write the following sets in the set-builder form :
(i){3, 6, 9, 12}
(ii) {2, 4, 8, 16, 32}
(iii) (5, 25, 125, 625}
(iv) (2, 4, 6, ...............}
(v) (1, 4, 9, ............... 100}
Solution:
Following are the set-builder form of sets :
(i) 3,6,9 and 12 are elements of (3, 6,9,12} and all of these are multiplies of 3. e.g.,
3 = 3 × 1
6 = 3 × 2
9 = 3 × 3
12 = 3 × 4 → 3n, where n is a natural number.
Thus, {3, 6, 9, 12}
= {x: x = 3n whereas n ∈ N, 1 ≤ n ≤ 4}

(ii) 2,4, 8,16 and 32 are elements of {2,4, 8,16,32}.
Now 2¹ = 2
2² = 4
2³ = 8
2⁴ = 16
2⁵ = 32
Thus, {2,4,8,16,32} = {x:x = 2ⁿ,whereas 1 ≤ n ≤ 5 where n is natural number}

(iii) 5,25,125 and 625 are elements of {5, 25, 125, 625}
Now, 5¹ =5
5⁵ = 25
5³ = 125
5⁴ = 625
Thus, {5, 25, 125, 625} = {x : x = 5ⁿ, whereas 1 ≤ n ≤ 4 where n is natural number}

(iv) 2, 4, 6 are elements of {2, 4, 6,......................} which are infinite and
2 = 2 × 1
4 = 2 × 2
6 = 2 × 3 ...... all are multiples of 2.
Thus, {2,4, 6, ............} = {x :x = 2ⁿ, n ∈ N}.
or {2,4,6, ..........} = {x: x are even natural numbers}

(v) 1, 4, 9, 16, 25, 36, 49, 64, 81 and 100 are elements of {1,4,9,.... 100}
Now, 1² = 1 .
2² = 4
3² = 9
4² = 16,
10² = 100
or
(-1)² = 1,
(-2)² = 4,
(-3)² = 9.
(-10)² = 100
{1, 4, 9, ...............100} = {x :x = n², whereas -10 ≤ n ≤ 10 where n is an integer}
or {1, 4, 9, 100} = {x : x = n² whereas 1 ≤ n ≤ 10
where n is natural number}

Question 5.
List all the elements of the following sets :
(i) A = {x : x is an odd natural number}
(ii) B = (x: x is an integer, \(\frac{1}{2}\) < x < \(\frac{9}{2}\)
(iii) C = (x : x is an integer, x² ≤ 4}
(iv) D = (x: x is a letter in the word “LOYAL”}
(v) E = ( x : x is a month of a year not having 31 days}
(vi) F = (x: x is a consonant in the English alphabet which precedes k}
Answer:
(i) A = { x : x is an odd natural number}
We know that 1, 3, 5, 7, 9, 11 are infinite odd natural numbers. So, listed form of above set will be A = {1, 3, 5, 7, 9, 11,....}

(ii) B = {x: x is an integer \(\frac{1}{2}\) < x < \(\frac{9}{2}\)}
We know that 0, 1,2, 3, and 4 are integers between - \(\frac{1}{2}\) and \(\frac{9}{2}\) as shown on number line.

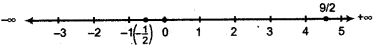
Thus, B = { 0,1,2,3,4} is listed form of given set B.

(iii) C = {x: x is an integer, x2 < 4}
We see that square of any integer which is equal to or less than 4 is as follows : (-2)² =4, (-1)² =1, 0² = 0 1² = 1, 2² = 4
We see that integers having square as 4 or less than 4 are -2, - 1, 0, 1 and 2.
Thus, list form of set C will be as follows : C = {-2, -1, 0, 1, 2}

(iv) D = {x: x is a letter in the word ‘LOYAL’}
In word LOYAL, L is repeated two times so list form of given set will be
D = {L, O, Y, A}

(v) We know that months of the year not having 31 days are Feb, April, June, Sep, Nov
Thus, given set in listed from will be
E = {Feb, April, June, Sep, Nov}

(vi) Letters of English alphabet which occurs before K are a, b, c, d, e,f g, h, i ,j out of which b, c, d, f, g, h, 7 are constants so listed form is :
{b, c, d, f, g, h, j}
⇒ Set F= {b, c, d, fg, h, j}

Question 6.
Match each of the set on the leftln the roster form with the same set on the right. described in set-builder form:

Answer:
(i) (1, 2, 3, 6} and (c) = {x : x is a natural number and is divisor of 6}
{1,2, 3,6} and (c)= {1,2, 3,6}
Both are same sets.

(ii) (2,3) and (a) = {x: x is a prime number and is divisor of 6} {2,3} and (a) = {2,3}
Both are same sets.

(iii) {M, A, T, H, E, I, C, S} and (d) = {x : x is a letter of the word MATHEMATICS }
Both represents same sets.

(iv) {1, 3, 5, 7, 9} and (b) {x : x is a odd natural number less than 10}
{1, 3, 5, 7,9} and (b)={ 1,3, 5,7,9}
Both sets are same.