RBSE Solutions for Class 10 Maths Chapter 2 बहुपद Ex 2.4

Rajasthan Board RBSE Solutions for Class 10 Maths Chapter 2 बहुपद Ex 2.4 Textbook Exercise Questions and Answers.

RBSE Class 10 Maths Solutions Chapter 2 बहुपद Ex 2.4

प्रश्न 1.
सत्यापित कीजिए कि निम्न त्रिघात बहुपदों के साथ दी गई संख्याएँ उसकी शून्यक हैं। प्रत्येक स्थिति में शून्यकों और गुणांकों के बीच के सम्बन्ध को भी सत्यापित कीजिए :
(i) 2x³ + x² - 5x + 2, \(\frac{1}{2}\), 1, -2
हल-
दिये गये बहुपद की बहुपद ax³ + bx² + cx + d के साथ तुलना करने पर,
a = 2, b = 1, c = -5 तथा d = 2

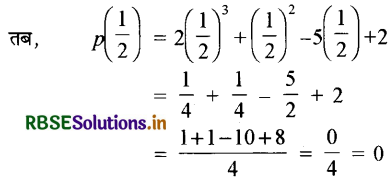
∴ \(\frac{1}{2}\), बहुपद p(x) का एक शून्यक है।
p(1) = 2(1)³ + (1)² - 5(1) + 2
= 2 + 1 - 5 + 2
= 0
इसी प्रकार
p(-2) = 2(-2)³ + (-2)² - 5(-2) + 2
= 2(-8) + 4 + 10 + 2
= -16 + 16
= 0
अर्थात् \(\frac{1}{2}\), 1 तथा -2 दिये गए बहुपद 2x³ + x² - 5x + 2 के शून्यक हैं।
अर्थात् α = \(\frac{1}{2}\), β = 1 तथा γ = -2 होगा।
तब शून्यकों का योग

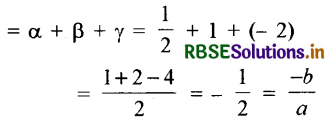
तथा दो शून्यकों को साथ लेकर उनके गुणनफलों का योग = αβ + βγ + γα

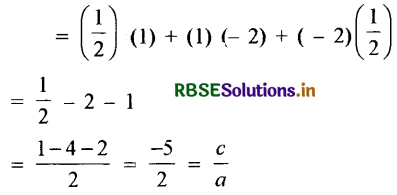
तथा शून्यकों का गुणनफल = αβγ
= \(\frac{1}{2}\) × 1 × 2
= -1
= \(\frac{-2}{2}\)
= \(\frac{-d}{a}\)
अतः शून्यकों \(\frac{1}{2}\), 1 व -2 द्वारा भी योगफल व गुणनफल वही है जो कि इनमें है।
∴ बहुपद के शून्यकों और गुणांकों के बीच सम्बन्ध सही है।

(ii) x³ - 4x² + 5x - 2; 2, 1, 1
हल-
दिये हुए बहुपद की 'बहुपद ax³ + bx² + cx + d के साथ तुलना करने पर,
a = 1, b = -4, c = 5 तथा d = -2
p(2) = (2)³ - 4(2)² + 5(2) - 2
= 8 - 16 + 10 - 2
= 0
अतः 2 बहुपद p(x) का शून्यक है।
p(1) = (1)³ - 4(1)² + 5(1) - 2
= 1 - 4 + 5 - 2
= 0
अर्थात् 2, 1 तथा 1 बहुपद x³ - 4x² + 5x - 2 के शून्यक हैं।
अतः, α = 2, β = 1 तथा γ = 1
इस प्रकार शून्यकों का योग = α + β + γ
= 2 + 1 + 1 
= 4 
= \(\frac{-(-4)}{1}\)
= \(\frac{-b}{a}\)
दो शून्यकों को साथ लेकर उनके गुणनफलों का योग = αβ + βγ + γα
= (2) (1) + (1) (1) + (1) (2)
= 2 + 1 + 2
= 5
= \(\frac{5}{1}\)
= \(\frac{c}{a}\)
तथा शून्यकों का गुणनफल = αβγ
= (2) (1) (1)
= 2
= \(\frac{-(-2)}{1}\)
= \(\frac{-d}{a}\)
∵ शून्यकों 2, 1, 1 से प्राप्त योगफल व गुणनफल भी यही है।
अतः बहुपद के शून्यकों का उनके गुणांकों से उक्त सम्बन्ध सत्य है।

प्रश्न 2.
एक विधात बहुपद प्राप्त कीजिए जिसके शून्यकों का योग, दो शून्यकों को एक साथ लेकर उनके गुणनफलों का योग तथा तीनों शून्यकों के गुणनफल क्रमशः 2, -7 व -14 हों।
हल-
माना कि त्रिघात बहुपदं ax³ + bx² + cx + d है तथा इसके शून्यक α, β तथा γ हैं।
तब शून्यकों का योग = α + β + γ
= 2
= \(\frac{-(-2)}{1}\)
= \(\frac{-b}{a}\)
दो शून्यकों को साथ लेकर उनके गुणनफलों का योग = αβ + βγ + γα
= -7
= \(\frac{-7}{1}\)
= \(\frac{c}{a}\)
तथा शून्यकों का गुणनफल = αβγ
= -14
=\( \frac{-14}{1}\)
= \(\frac{-d}{a}\)
यदि a = 1 और b = -2, c = -7 तथा d = 14 है।
इस प्रकार बहुपद x³ - 2x² - 7x + 14 बना।

प्रश्न 3.
यदि बहुपद x³ - 3x² + x + 1 के शून्यक a - b, a, a + b हों, तो a और b ज्ञात कीजिए।
हल-
∵ (a - b), a, (a + b) बहुपद x³ - 3x² + x + 1 के शून्यक हैं तब शून्यकों का योग = α + β + γ = \(-\frac{b}{a}\)
⇒ (a - b) + a + (a - b) = \(\frac{-(-3)}{1}\) = 3
⇒ 3a = 3
⇒ a = 1
दो शून्यकों को साथ लेकर उनके गुणनफलों का योग अर्थात्
αβ + βγ + γα = \(\frac{c}{a}\)
⇒ (a - b) a + a (a + b) + (a + b) (a - b) = \(\frac{1}{1}\) = 1
⇒ a² - ab + a² + ab + a² - b² = 1
⇒ 3a² - b² = 1
⇒ 3(1)² - b² = 1 [∵ a = 1]
⇒ 3 - b² = 1
⇒ b² = 2
⇒ b = ±√2
अतः, a = 1 और b = ±√2

प्रश्न 4.
यदि बहुपद x⁴ - 6x³ - 26x² + 138x - 35 के दो शून्यक 2 ± √3 हों, तो अन्य शून्यक ज्ञात कीजिए।
हल-
∵ बहुपद p(x) = x⁴ - 6x³ - 26x² + 138x - 35 के दो शून्यक 2 ± √3 हैं।
इसलिए, x = 2 ± √3
⇒ x - 2 = ±√3
दोनों पक्षों का वर्ग करने पर,
x² - 4x + 4 = 3
⇒ x² - 4x + 1 = 0
अब x² - 4x + 1 से बहुपद p(x) को भाग देने पर ताकि अन्य शून्यक प्राप्त हो सकें।

विभाजन एल्गोरिथ्म का प्रयोग करने पर
∴ p(x) = x⁴ - 6x³ - 26x² + 138x - 35
= (x² - 4x + 1) (x² - 2x - 35)
= (x² - 4x + 1) (x - 7x + 5x - 35)
= (x² - 4x + 1) [x(x - 7) + 5(x - 7)]
= (x² - 4x + 1) (x + 5) (x - 7)
= (x + 5) तथा (x - 7) अन्य गुणनखण्ड होंगे।
अतः -5 तथा 7 अन्य शून्यक होंगे।

प्रश्न 5.
यदि बहुपद x⁴ - 6x³ + 16x² - 25x + 10 को एक अन्य बहुपद x² - 2x + k से भाग दिया जाए और शेषफल x + a आता हो, तो k तथा a ज्ञात कीजिए।
हल-
बहुपद x⁴ - 6x³ + 16x² - 25x + 10 को बहुपद x² - 2x + k से भाग देने पर

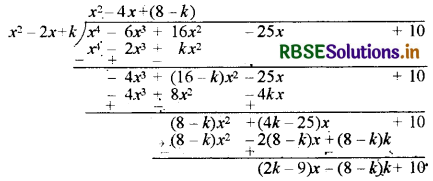
∴ शेषफल = (2k - 9) x - (8 - k) k + 10
परन्तु शेषफल = x + a
इसलिए, गुणांकों की तुलना करने पर
2k - 9 = 1
⇒ 2k = 10
⇒ k = 5
तथा -(8 - k) k + 10 = a
a = -(8 - 5)5 + 10
= -3 × 5 + 10
= -15 + 10
= -5
अतः, k = 5 तथा a = -5