RBSE Solutions for Class 10 Maths Chapter 2 बहुपद Ex 2.3

Rajasthan Board RBSE Solutions for Class 10 Maths Chapter 2 बहुपद Ex 2.3 Textbook Exercise Questions and Answers.

RBSE Class 10 Maths Solutions Chapter 2 बहुपद Ex 2.3

प्रश्न 1.
विभाजन एल्गोरिथ्म का प्रयोग करके, निम्न में p(x) को g(x) से भाग देने पर भागफल तथा शेषफल ज्ञात कीजिए:
(i) p(x) = x³ - 3x² + 5x - 3, g(x) = x² - 2
हल-
दिया है, p(x) = x³ - 3x² + 5x - 3 तथा g(x) = x² - 2
माना भागफल q(x) और शेषफल r(x) हो तो यूक्लिड विभाजन एल्गोरिथ्म से,

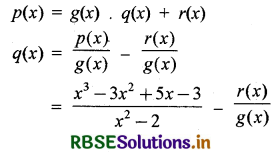
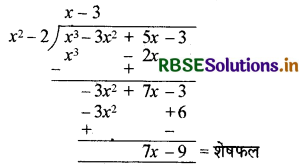
∴ भागफल q(x) = x - 3,
शेषफल r(x) = 7x - 9

(ii) p(x) = x⁴ - 3x² + 4x + 5, g(x) = x² + 1 - x
हल-
दिया गया है,
p(x) = x⁴ - 3x² + 4x + 5, g(x) = x² + 1 - x = x² - x + 1
माना भागफल q(x) तथा शेषफल r(x) हो तो यूक्लिड विभाजन एल्गोरिथ्म से,

∴ भागफल g(x) = x² + x - 3 तथा शेषफल r(x) = 8 होगा।

(iii) p(x) = x⁴ - 5x + 6, g(x) = 2 - x²
हल-
दिया गया है,
p(x) = x⁴ - 5x + 6
g(x) = 2 - x²
माना भागफल q(x) तथा शेषफल r(x) है। तब यूक्लिड विभाजन एल्गोरिथम से,

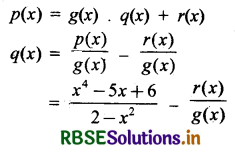
अतः भागफल q(x) = -x² - 2 तथा शेषफल r(x) = -5x + 10

प्रश्न 2.
पहले बहुपद से दूसरे बहुपद को भाग करके, जाँच कीजिए कि क्या प्रथम बहुपद, द्वितीय बहुपद का एक गुणनखण्ड है :
(i) t² - 3, 2t⁴ + 3t³ - 2t² - 9t - 12
हल-
2t⁴ + 3t³ - 2t² - 9t - 12 को t² - 3 से भाग करने पर

चूँकि, शेषफल शून्य है, अतः t² - 3 बहुपद 2t⁴ + 3t³ - 2t² - 9t - 12 का एक गुणनखण्ड है।

(ii) x² + 3x + 1, 3x⁴ + 5x³ - 7x² + 2x + 2
हल-
3x⁴ + 5x³ - 7x² + 2x + 2 को x² + 3x + 1 से भाग करने पर

चूँकि, शेषफल शून्य है, अतः x² + 3x + 1 बहुपद 3x⁴ + 5x³ - 7x² + 2x + 2 का एक गुणनखण्ड है।

(iii) x³ - 3x + 1, x⁵ - 4x³ + x² + 3x + 1
हल-
x⁵ - 4x³ + x² + 3x + 1 बहुपद को x³ - 3x + 1 से भाग करने पर

यहाँ शेषफल 2 है अर्थात् शेषफल शून्य नहीं है अतः x³ - 3x + 1 बहुपद x⁵ - 4x³ + x² + 3x + 1 का गुणनखण्ड नहीं है।

प्रश्न 3.
3x⁴ + 6x³ - 2x² - 10x - 5 के अन्य सभी शून्यक ज्ञात कीजिए यदि इसके दो शून्यक \(\sqrt{\frac{5}{3}}\) और \(-\sqrt{\frac{5}{3}}\) है।
हल-
चूँकि, दो शून्यक \(\sqrt{\frac{5}{3}}\) एवं \(-\sqrt{\frac{5}{3}}\) है तो (x - \(\sqrt{\frac{5}{3}}\)) एवं (x + \(\sqrt{\frac{5}{3}}\)) दिये गये बहुपदों के गुणनखण्ड होंगे।
अतः \(\left(x-\sqrt{\frac{5}{3}}\right)\left(x+\sqrt{\frac{5}{3}}\right)=x^{2}-\frac{5}{3}\)
(3x² - 5) दिये गये बहुपद का गुणनखण्ड होगा।
3x² - 5 से बहुपद 3x⁴ + 6x³ - 2x² - 10x - 5 को भाग करने पर

अतः, 3x⁴ + 6x³ - 2x² - 10x - 5 = (3x² - 5)(x² + 2x + 1)
अब, x² + 2x + 1 = x² + x + x + 1
= x(x + 1) + 1(x + 1)
= (x + 1) (x + 1)
अतः इसके अन्य शून्यक -1 और -1 होंगे।
इस प्रकार, चतुर्थ घातांक बहुपद के सभी शून्यक \(\sqrt{\frac{5}{3}}\), \(-\sqrt{\frac{5}{3}}\), -1 और -1 होंगे।

प्रश्न 4.
यदि x³ - 3x² + x + 2 को एक बहुपद g(x) से भाग देने पर, भागफल और शेषफल क्रमशः x - 2 और -2x + 4 हैं तो g(x) ज्ञात कीजिए।
हल-
बहुपद x³ - 3x² + x + 2 को एक बहुपद g(x) से भाग देने पर भागफल (x - 2) व शेषफल -2x + 4 प्राप्त होता है।
∴ भाज्य = भाजक × भागफल + शेषफल
या (x - 2) × g(x) + (-2x + 4) = x³ - 3x² + x + 2
या (x - 2) × g(x) = x³ - 3x² + x + 2 + 2x - 4
या g(x) = \(\frac{x^{3}-3 x^{2}+3 x-2}{x-2}\)
अब, बहुपद x³ - 3x² + 3x - 2 को x - 2 से भाग देने पर

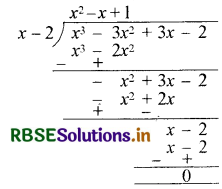
अतः, g(x) = x² - x + 1 प्राप्त होगा।

प्रश्न 5.
बहुपदों p(x), g(x), q(x) और r(x) के ऐसे उदाहरण दीजिए जो विभाजन एल्गोरिथ्म को सन्तुष्ट करते हों तथा
(i) घात p(x) = घात q(x)
हल-
हमें p(x) व q(x) ऐसा चाहिये कि p(x) की घात = q(x) की घात 
तब p(x) की घात = q(x) की घात . q(x) की घात
⇒ g(x) की घात शून्य होनी चाहिए।
माना कि p(x) = 5x² - 5x + 10, g(x) = 5
q(x) = x² - x + 2; r(x) = 0

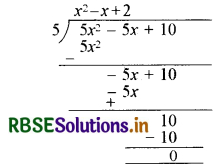
विभाजन एल्गोरिथ्म से,
5x² - 5x + 10 = 5(x² - x + 2) + 0
p(x) = g(x) . q(x) + r(x)
अतः p(x) की घात = q(x) की घात = 2

(ii) घात q(x) = घात r(x)
हल-
q(x) की घात = r(x) की घात
p(x) = g(x) . q(x) + r(x)
p(x) की घात, g(x) की घात व q(x) की घात के योग के बराबर होना चाहिए।
माना कि p(x) = 7x³ - 42x + 53
g(x) = x³ - 6x + 7
q(x) = 7
r(x) = 4

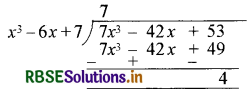
∴ विभाजन एल्गोरिथ्म से,
7x³ - 42x + 53 = 7(x³ - 6x + 7) + 4
p(x) = q(x) . g(x) + r(x)
अतः q(x) की घात = शून्य

(iii) घात r(x) = 0
हल-
घात r(x) = 0
माना p(x) = x + 2
और g(x) = x² - x + 1
⇒ x³ + 2 में x² - x + 1 से भाग देने पर

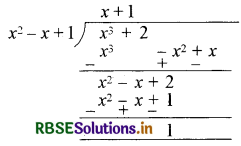
विभाजन एल्गोरिथ्म से,
x³ + 2 = (x² - x + 1) (x + 1) + 1
p(x) = g(x) . q(x) + r(x)
साथ ही घात r(x) = 0