RBSE Solutions for Class 10 Maths Chapter 11 रचनाएँ Ex 11.2

Rajasthan Board RBSE Solutions for Class 10 Maths Chapter 11 रचनाएँ Ex 11.2 Textbook Exercise Questions and Answers.

RBSE Class 10 Maths Solutions Chapter 11 रचनाएँ Ex 11.2

निम्न में से प्रत्येक के लिए रचना का औचित्य भी दीजिए:

11.2 Class 10 Maths In Hindi प्रश्न 1.
6 cm त्रिज्या का एक वृत्त खींचिए। केन्द्र से 10 cm दूर स्थित एक बिन्दु से वृत्त पर स्पर्श रेखा युग्म की रचना कीजिए और उनकी लम्बाइयाँ मापिए।
हल-
रचना के चरण :
1. सर्वप्रथम O बिन्दु को केन्द्र लेकर 6 cm त्रिज्या का एक वृत्त खींचिए।
2. केन्द्र O से 10 cm दूर P बिन्दु अंकित कीजिए।
3. अब OP को मिलाकर इसे समद्विभाजित कीजिए। इसके मध्य बिन्दु को M से अंकित कीजिए।
4. M को केन्द्र और MP को त्रिज्या मानकर एक वृत्त खींचिए जो वृत्त को Q और R पर प्रतिच्छेदित करते हैं।
5. PQ और PR को मिलाइए। तब, PQ और PR अभीष्ट स्पर्श रेखाएँ हैं।
मापने पर PQ = PR = 8 cm

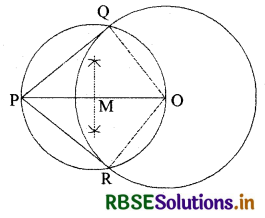
स्पष्टीकरण-
OQ को जोड़ने पर ∠PQO = 90°, क्योंकि ∠PQO अर्द्धवृत्त में बना कोण है।
∴ PQ ⊥ OQ
चूँकि OQ दिए गए वृत्त की त्रिज्या है, अतः PQ वृत्त की स्पर्श रेखा होगी। उसी तरह, PR भी वृत्त की स्पर्श रेखा होगी।

10th Class Math 11.2 In Hindi प्रश्न 2.
4 cm त्रिज्या के एक वृत्त. पर 6 cm त्रिज्या के एक संकेन्द्रीय वृत्त के किसी बिन्दु से एक स्पर्श रेखा की रचना कीजिए और उसकी लम्बाई मापिए। परिकलन से इस माप की जाँच भी कीजिए।
हल-
रचना के चरण :
1. सर्वप्रथम O बिन्दु से 4 cm और 6 cm त्रिज्या के दो संकेन्द्रीय वृत्त खींचिए।
2. बड़े वृत्त की परिधि पर बिन्दु P अंकित कीजिए।
3. अब OP को जोड़कर इसे समद्विभाजित कीजिए। M को इसका मध्य बिन्दु मान लीजिए।
4. M केन्द्र से MP त्रिज्या का एक वृत्त खींचिए जो वृत्त को Q और R पर प्रतिच्छेदित करें।
5. PQ और PR को मिलाइए। तब PO और PR वांछित स्पर्श रेखाएँ हैं।
मापने पर PQ = PR = 4.5 cm (लगभग)

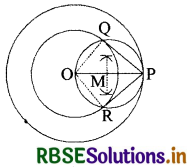
स्पष्टीकरण-
OQ को मिलाने पर, ∠PQO = 90° क्योंकि ∠PQO अर्द्धवृत्त में बना कोण है।
∴ PQ ⊥ OQ
चूँकि OQ दिए हुए वृत्त की त्रिज्या है, अतः PQ वृत्त की स्पर्श रेखा होगी। इसी प्रकार, PR भी वृत्त की स्पर्श रेखा होगी।
स्पर्श रेखा की लम्बाई मापने पर PQ = PR = 4.5 cm
परिकलन-
स्पर्श रेखा PQ = \(\sqrt{(O P)^{2}-(O Q)^{2}}\)
= \(\sqrt{(6)^{2}-(4)^{2}}\)
= \(\sqrt{36-16}\)
= \(\sqrt{20}\)
= 4.47 cm
≅ 4.5 cm

Class 10 Maths 11.2 Solutions In Hindi प्रश्न 3.
3 cm त्रिज्या का एक वृत्त खींचिए। इसके किसी बढ़ाए गए व्यास पर केन्द्र से 7 cm की दूरी पर स्थित दो बिन्दु P और Q लीजिए। इन दोनों बिन्दुओं से वृत्त पर स्पर्श रेखाएँ खींचिए।
हल-
रचना के चरण :
1. सर्वप्रथम O बिन्दु लें, इसे केन्द्र मानकर 3 cm त्रिज्या का एक वृत्त खींचिए।
2. इसके बढ़ाए गए व्यास पर दो बिन्दु P और Q लीजिए। इस तरह OP = OQ = 7 cm.
3. अब OP और OQ को समद्विभाजित कीजिए। इनके मध्य बिन्दु क्रमशः M₁ और M₂ लीजिए।
4. M₁ को केन्द्र व M₁P को त्रिज्या मानकर एक वृत्त खींचिए, जो वृत्त को T₁ और T₂ पर प्रतिच्छेदित करे।
5. PT₁ और PT₂ को मिलाइए। फिर PT₁ और PT₂ वांछित स्पर्श रेखाएँ हैं।
इसी प्रकार QT₃ और QT₄ स्पर्श रेखाएँ प्राप्त की जा सकती हैं।

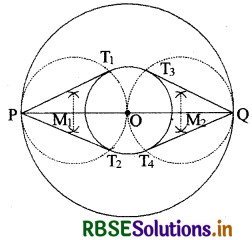
स्पष्टीकरण-
OT₁ को मिलाने पर ∠PT₁O = 90°, क्योंकि यह अर्द्धवृत्त में बना कोण है।
∴  PT₁ ⊥ OT₁
चूँकि OT₁ दिए गए वृत्त की त्रिज्या है, अत: PT₁ वृत्त की स्पर्श रेखा होगी।
इसी प्रकार PT₂, QT₃ और QT₄ भी वृत्त की स्पर्श रेखाएँ होंगी।

Class 10 Maths Chapter 11 Exercise 11.2 In Hindi प्रश्न 4.
5 cm त्रिज्या के एक वृत्त पर ऐसी दो स्पर्श रेखाएँ खींचिए, जो परस्पर 60° के कोण पर झुकी हों।
हल-
रचना के चरण :
1. सर्वप्रथम O केन्द्र व 5 cm की त्रिज्या से एक वृत्त खींचिए।
2. कोई भी व्यास AOC खींचिए।
3. अब त्रिज्या OL ऐसे खींचिए कि ∠COL = 60° (अर्थात् दिया गया कोण) हो।
4. L पर LM ⊥ OL खींचिए।
5. A पर AN ⊥ OA खींचिए।
6. ये दोनों लम्ब परस्पर P बिन्दु पर प्रतिच्छेदित करते हैं। तब PA और PL वांछित स्पर्श रेखाएँ होंगी।

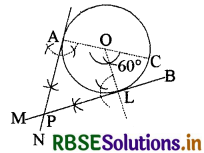
स्पष्टीकरण-
चूँकि OA त्रिज्या है, अत: PA वृत्त की स्पर्श रेखा होगी। इसी प्रकार, PL भी वृत्त की त्रिज्या होगी।
∠APL = 360° - ∠OAP - ∠OLP - ∠AOL
= 360° - 90° - 90° - (180° - 60°)
= 360° - 360° + 60°
= 60°
इस प्रकार स्पर्श रेखाएँ PA और PL परस्पर 60° के कोण पर झुकी होंगी।

Class 10th Maths Chapter 11 Exercise 11.2 In Hindi प्रश्न 5.
8 cm लम्बा एक रेखाखण्ड AB खींचिए। A को केन्द्र मानकर 4 cm त्रिज्या का एक वृत्त तथा B को केन्द्र लेकर 3 cm त्रिज्या का एक अन्य वृत्त खींचिए। प्रत्येक वृत्त पर दूसरे वृत्त के केन्द्र से स्पर्श रेखाओं की रचना कीजिए।
हल-
रचना के चरण :
1. सर्वप्रथम रेखाखण्ड AB = 8 cm खींचिए।
2. अब A को केन्द्र लेकर 4 cm त्रिज्या का एक वृत्त खींचिए और B को केन्द्र मानकर 3 cm त्रिज्या का एक वृत्त खींचिए। AB को समद्विभाजित करके मध्य बिन्दु O ज्ञात किया।
3. स्पष्ट है कि O, AB का मध्य-बिन्दु है। O केन्द्र से OA या OB त्रिज्या का एक वृत्त खींचिए जो B केन्द्र वाले वृत्त को T₁ और T₂ पर और A केन्द्र वाले वृत्त को T₃ और T₄ पर प्रतिच्छेदित करे।
4. AT₁, AT₂, BT₃, और BT₄, को मिलाइए। तब ये वांछित स्पर्श रेखाएँ होंगी।

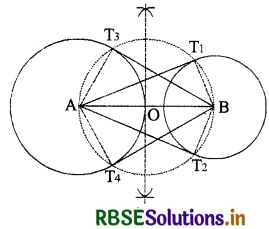
स्पष्टीकरण-
BT₁ को मिलाने पर BT₁A = 90°, क्योंकि, ∠BT₁A अर्द्धवृत्त में स्थित कोण है।
∴ AT₁ ⊥ BT₁
चूँकि BT₁ दिए गए वृत्त की त्रिज्या है, अतः AT₁ वृत्त की स्पर्श रेखा होगी।
इसी प्रकार, AT₂, BT₃ और BT₄ भी स्पर्श रेखाएँ होंगी।

प्रश्नावली 11.2 कक्षा 10 प्रश्न 6.
माना ABC एक समकोण त्रिभुज है, जिसमें AB = 6 cm, BC = 8 cm तथा ∠B = 90° है। B से AC पर BD लम्ब है। बिन्दुओं B, C, D से होकर जाने वाला एक वृत्त खींचा गया है। A से इस वृत्त पर स्पर्श रेखा की रचना कीजिए।
हल-
रचना के चरण :
1. सर्वप्रथम दिए गए मान से एक ∆ABC की रचना कीजिए जिसमें AB = 6 cm, BC = 8 cm और ∠B = 90° हो।
2. BD ⊥ AC खींचिए।
3. अब D केन्द्र और DA, DB या DC त्रिज्या से एक वृत्त खींचिए।

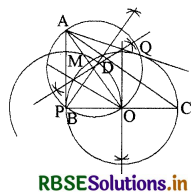
4. BC और BD का लम्बअर्धक करते हैं जो कि बिन्दु O पर प्रतिच्छेद होते हैं।
5. O को केन्द्र मानकर OB त्रिज्या का एक वृत्त खींचते हैं। यह वृत्त बिन्दु B, C तथा D से होकर जाता है।
6. OA को मिलाया गया है।
7. OA का लम्बअर्धक कीजिये। यह लम्बअर्धक M बिन्दु पर प्राप्त होता है।
8. M को केन्द्र मानकर MA त्रिज्या का एक वृत्त खींचते हैं जो कि P तथा Q बिन्दु पर प्रतिच्छेद होता है।
9. AP तथा AQ को मिलाया गया है जो कि A से इस वृत्त पर अभीष्ट स्पर्श रेखाएँ हैं।

कक्षा 10 गणित प्रश्नावली 11.2 प्रश्न 7.
किसी चूड़ी की सहायता से एक वृत्त खींचिए। वृत्त के बाहर एक बिन्दु लीजिए। इस बिन्दु से वृत्त पर स्पर्श रेखाओं की रचना कीजिए।
हल-
रचना के चरण :
1. सर्वप्रथम एक चूड़ी की सहायता से एक वृत्त खींचिए।
2. बाहरी बिन्दु A से एक छेदक रेखा ARS खींचिए। RA को C तक ऐसे बढ़ाइए कि AR = AC हो जाए।

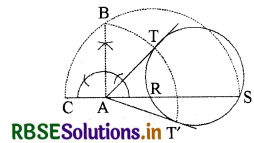
3. अब CS को व्यास लेकर एक अर्द्धवृत्त खींचिए।
4. A बिन्दु पर AB ⊥ AS खींचिए जो अर्द्धवृत्त को B पर काटे।
5. A केन्द्र से और AB त्रिज्या से एक चाप खींचिए जो दिए हुए वृत्त को T और T' पर काटे। AT और AT' को मिला दीजिए। तब, AT और AT' अभीष्ट रेखाएँ होंगी।