RBSE Class 12 Physics Notes Chapter 8 वैद्युतचुंबकीय तरंगें

These comprehensive RBSE Class 12 Physics Notes Chapter 8 वैद्युतचुंबकीय तरंगें will give a brief overview of all the concepts.

RBSE Class 12 Physics Chapter 8 Notes वैद्युतचुंबकीय तरंगें

→ विद्युत्-चुम्बकीय तरंगें:
आकाश (space) में समय के साथ परिवर्ती विद्युत् व चुम्बकीय क्षेत्रों का तरंग रूप में संचरण ही विद्युत्-चुम्बकीय तरंग कहलाता है।

→ मैक्सवेल के समीकरण (Maxwell's equation):
मैक्सवेल के निम्नांकित चार समीकरण हैं
(i) स्थिर वैद्युत का गाउस नियम : .
\(\oint_{\mathrm{s}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d s}=\frac{q}{\varepsilon_0}\)

(ii) स्थिर चुम्बकत्व का गाउस नियम :
\(\oint_{\mathrm{s}} \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d s}\) = 0

(iii) फैराडे का विद्युत्-चुम्बकीय प्रेरण का नियम :
e = \(\oint_{\mathrm{C}} \overrightarrow{\mathrm{B}} \cdot d \vec{l}=-\frac{d \phi_m}{d t}\)

(iv) ऐम्पियर का संशोधित नियम
\(\oint_{\vec{B} \cdot d \vec{l}}\) = μ₀(I_C + I_D)
= μ₀(I_C + ε₀\(\frac{\partial \phi_{\mathrm{E}}}{\partial t}\))

→ विद्युत्-चुम्बकीय तरंगों के अभिलक्षण (Characteristics):
(i) इनके संचरण (propagation) के लिए माध्यम की आवश्यकता नहीं होती है।

(ii) ये प्रकाश की चाल (c = 3 × 10⁸ ms^-1) से चलती हैं।

(iii) विद्युत्-चुम्बकीय तरंगें अनुप्रस्थ होती हैं। इनमें विद्युत् एवं चुम्बकीय क्षेत्र तरंग संचरण की दिशा के लम्बवत् एवं परस्पर भी लम्बवत् रहते हैं।
(iv) किसी माध्यम में विद्युत्-चुम्बकीय तरंगों की चाल
v = \(\frac{1}{\sqrt{\mu . \varepsilon}}=\frac{1}{\sqrt{\mu_r \cdot \mu_0 \varepsilon_r \cdot \varepsilon_0}} = \frac{c}{\sqrt{\mu_r \cdot \varepsilon_r}}=\frac{c}{n}\)
जहाँ n माध्यम का अपवर्तनांक है।

(v) विद्युत्-चुम्बकीय तरंग का औसत ऊर्जा घनत्व (Average energy density)

(u_e)_av = (u_m)_av
⇒ \(\frac{1}{2}\)ε₀E_rms² = \(\frac{\mathrm{B}_{\mathrm{rms}}^2}{2 \mu_0}\)
कुल ऊर्जा घनत्व u_av = u_e + u_m
= \(\frac{1}{2}\)ε₀E₀²

(vi) विद्युत्-चुम्बकीय तरंगों द्वारा डाला गया दाब अर्थात् farohen gra (Radiation pressure)

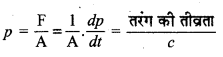
(vii) विद्युत्-चुम्बकीय तरंगें परावर्तन, अपवर्तन, विवर्तन, व्यतिकरण आदि घटनाओं को प्रदर्शित करती हैं।

→ विद्युत् व चुम्बकीय क्षेत्रों के परिमाणों (magnitudes) में सम्बन्ध
\(\frac{E_0}{B_0}\) = c = प्रकाश की चाल = \(\frac{1}{\sqrt{\mu_0 \varepsilon_0}}\)

→ विद्युत्-चुम्बकीय तरंग की तीव्रता-तरंग संचरण की दिशा के लम्बवत् एकांक क्षेत्रफल से प्रति सेकण्ड स्थानान्तरित ऊर्जा को तरंग की तीव्रता कहते हैं। इसे I से व्यक्त करते हैं।
I = \(\frac{1}{2}\)ε₀.c.E₀²

→ गाउस नियम \(\oint_S \overrightarrow{\mathrm{E}} \cdot d \vec{s}=\frac{q}{\varepsilon_0}\)

→ स्थिर चुम्बकत्व का गाउस का नियम \(\oint \overrightarrow{\mathrm{B}} \cdot d \vec{s}\) = 0

→ फैराडे का विद्युत्-चुम्बकीय प्रेरण का \(\oint_C \overrightarrow{\mathrm{E}} \cdot d \vec{l}=-\frac{d \phi_m}{d t}\)

→ ऐम्पियर का संशोधित नियम
\(\oint_S \overrightarrow{\mathrm{B}} \cdot d \vec{l} \)= μ₀(I_C + I_D) = μ₀(I_C + ε₀\(\frac{d \phi_{\mathrm{E}}}{d t}\))

→ ऊर्जा घनत्व u_E = \(\frac{1}{2}\)ε₀.c.E²
u_B = \(\frac{\mathrm{B}^2}{2 \mu_0}\)

→ विद्युत् चुम्बकीय तरंगों का तीव्रता घनत्व
I = \(\frac{1}{2}\)ε₀cE² = \(\frac{1}{2}\)ε₀cE₀²

→ विद्युत एवं चुम्बकीय क्षेत्र में सम्बन्ध
\(\frac{\mathrm{E}_0}{\mathrm{~B}_0}\) = c

→ विकिरण दाब P = \(\frac{\mathrm{F}}{\mathrm{A}}=\frac{1}{\mathrm{~A}} \frac{d p}{d t}\)

→ पाइन्टिंग सदिश \(\vec{p}=\overrightarrow{\mathrm{E}} \times \overrightarrow{\mathrm{H}}\)

→ प्वांइटिंग सदिश (Poynting vector):
तरंग द्वारा प्रति इकाई क्षेत्र से स्थानान्तरित ऊर्जा प्वाइटिंग सदिश कहलाती है।

→ तरंग की तीव्रता (Intensity of wave):
तरंगों की तीव्रता से तात्पर्य उस ऊर्जा प्रवाह की दर से है जो तरंगों के संचरण की दिशा के लम्बवत् रखे एकांक क्षेत्रफल के समतल से प्रवाहित हो रही है।

→ कम्पन तल (Vibration plane):
विद्युत् क्षेत्र सदिश E जिस तल में कम्पन करता है उसे कम्पन तल कहते हैं।

→ ध्रुवण तल (Polorisation plane):
वह तल जिसमें चुम्बकीय क्षेत्र सदिश B कम्पन करता है; उसे ध्रुवण तल कहते हैं।